Интегрирование по частям определённого интеграла
Если функции 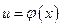 и
и 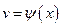 непрерывны на отрезке
непрерывны на отрезке 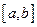 вместе со своими производными, то справедлива формула интегрирования по частям:
вместе со своими производными, то справедлива формула интегрирования по частям:

Вывод этой формулы абсолютно аналогичен выводу формулы интегрирования по частям для неопределенного интеграла, который был весьма подробно рассмотрен выше.
Приближенное вычисление определенного интеграла
Существует большое число функций, интеграл от которых не может быть выражен через элементарные функции. Для нахождения интегралов от подобных функций применяются разнообразные приближенные методы, суть которых заключается в том, что подинтегральная функция заменяется “близкой” к ней функцией, интеграл от которой выражается через элементарные функции.
Формула прямоугольников
Если известны значения функции 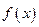 в некоторых точках
в некоторых точках 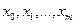 , то в качестве функции аппроксимирующей
, то в качестве функции аппроксимирующей 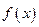 можно взять многочлен
можно взять многочлен 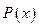 степени не выше
степени не выше  , значения которого в выбранных точках равны значениям функции f(x) в этих точках.
, значения которого в выбранных точках равны значениям функции f(x) в этих точках.
 .
.
Разобьем отрезок интегрирования на 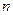 равных частей и положим
равных частей и положим  . При этом:
. При этом:
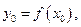
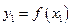 , …. ,
, …. ,  .
.
Составим суммы 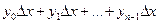 ;
;  - соответственно нижнюю и верхнюю интегральные суммы. Первая соответствует вписанной ломаной, вторая – описанной. Тогда
- соответственно нижнюю и верхнюю интегральные суммы. Первая соответствует вписанной ломаной, вторая – описанной. Тогда
 или
или 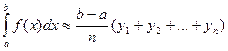 -
-
любая из этих формул может применяться для приближенного вычисления определенного интеграла и называется общей формулой прямоугольников.
Формула трапеций
Эта формула является более точной по сравнению с формулой прямоугольников. Подынтегральная функция в этом случае заменяется на вписанную ломаную.
 y
y
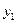


a 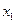
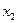 b x
b x
Геометрически площадь криволинейной трапеции заменяется суммой площадей вписанных трапеций. Очевидно, что чем больше взять точек 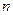 разбиения интервала, тем с большей точностью будет вычислен интеграл.
разбиения интервала, тем с большей точностью будет вычислен интеграл.
Площади вписанных трапеций вычисляются по формулам:
 ;
;
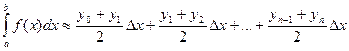 .
.
После приведения подобных слагаемых получаем формулу трапеций:

Формула парабол
(формула Симпсона или квадратурная формула).
Разделим отрезок интегрирования 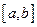 на четное число отрезков
на четное число отрезков 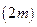 . Площадь криволинейной трапеции, ограниченной графиком функции
. Площадь криволинейной трапеции, ограниченной графиком функции 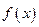 заменим на площадь криволинейной трапеции, ограниченной параболой второй степени с осью симметрии, параллельной оси Оу и проходящей через точки кривой, со значениями
заменим на площадь криволинейной трапеции, ограниченной параболой второй степени с осью симметрии, параллельной оси Оу и проходящей через точки кривой, со значениями 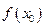 ,
,  ,
, 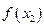 . Для каждой пары отрезков построим такую параболу.
. Для каждой пары отрезков построим такую параболу.
 |
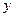
0 
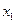
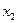
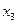
 х
х
Уравнения этих парабол имеют вид 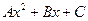 , где коэффициенты
, где коэффициенты  могут быть легко найдены по трем точкам пересечения параболы с исходной кривой.
могут быть легко найдены по трем точкам пересечения параболы с исходной кривой.
 (6.1)
(6.1)
Обозначим 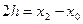 .
.
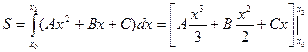 .
.
Если принять 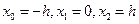 , то
, то 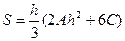 (6.2)
(6.2)
Тогда уравнения значений функции (6.1) имеют вид:
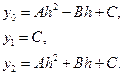
C учетом этого:  .
.
Отсюда уравнение (6.2) примет вид: 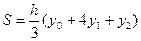 .
.
Тогда
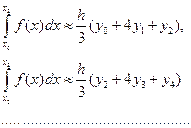
Складывая эти выражения, получаем формулу Симпсона:
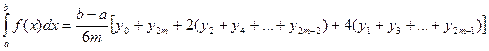 .
.
Чем больше взять число  , тем более точное значение интеграла будет получено.
, тем более точное значение интеграла будет получено.
Пример. Вычислить приближенное значение определенного интеграла
 с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. По формуле Симпсона получим:
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. По формуле Симпсона получим:

| m | |||||||||||
| x | -2 | -1 | |||||||||
| f(x) | 2.828 | 3.873 | 4.123 | 4.899 | 6.557 | 8.944 | 11.874 | 15.232 | 18.947 | 22.978 |

Точное значение этого интеграла – 91.173.
Как видно, даже при сравнительно большом шаге разбиения точность полученного результата вполне удовлетворительная.
Для сравнения применим к этой же задаче формулу трапеций.
 Формула трапеций дала менее точный результат по сравнению с формулой Симпсона.
Формула трапеций дала менее точный результат по сравнению с формулой Симпсона.
Кроме вышеперечисленных способов, можно вычислить значение определенного интеграла с помощью разложения подынтегральной функции в степенной ряд.
Принцип этого метода состоит в том, чтобы заменить подынтегральную функцию по формуле Тейлора и почленно проинтегрировать полученную сумму.
Пример. С точностью до 0,001 вычислить интеграл
 .
.
Так как интегрирование производится в окрестности точки  , то можно воспользоваться для разложения подынтегральной функции формулой Маклорена.
, то можно воспользоваться для разложения подынтегральной функции формулой Маклорена.
Разложение функции  имеет вид:
имеет вид:
 .
.
Зная разложение функции  легко найти функцию
легко найти функцию  :
:
 .
.
Теперь представим в виде ряда подынтегральное выражение:
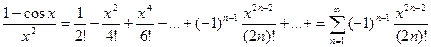 .
.
Теперь представим наш интеграл в виде:
 .
.
Применим теорему о почленном интегрировании ряда. (Т.е. интеграл от суммы будет представлен в виде суммы интегралов членов ряда).
Вообще говоря, со строго теоретической точки зрения для применения этой теоремы надо доказать, что ряд сходится равномерно на отрезке интегрирования 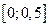 .
.
Таким образом
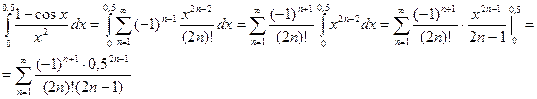
Получаем:

Как видно, абсолютная величина членов ряда очень быстро уменьшается, и требуемая точность достигается уже при третьем члене разложения.
Более точное значение этого интеграла: 0,2482725418…
