Принцип наименьшего действия

Принцип наименьшего действияявляется основным, как в механике, так и в теории поля. Смысл его состоит в том, что реально осуществляемое движение или распределение поля отличается от всех других -физически нереализуемых, невозможных, тем, что сообщает экстремум некоторому положительнозначному функционалу, который называется действием. Этот принцип имеет многочисленные проявления. Например, луч света в однородном пространстве распространяется по прямой. Известно, что прямая - это как раз та линия между двумя точками, движение по которой осуществляется за наименьшее время (при постоянной скорости) в силу ее наименьшей длины среди всех иных линий, эти точки соединяющих.

Этот простой физический принцип имеет интересные и нетривиальные проявления в теории поля, и мы рассмотрим его более подробно.

Пусть имеется система из N материальных точек, каждая из которых обладает массой m_i и характеризуется положением в пространстве, задаваемым тремя координатами 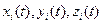, зависящими от времени t. Индекс i нумерует рассматриваемые материальные точки. Как известно, кинетическая энергиятакой системы определится выражением:

.

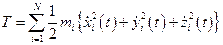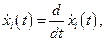
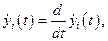
Здесь 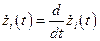- представляют собой компоненты скорости в направлении осей OX, OY,OZ соответственно.

Если движение системы осуществляется в интервале времени 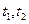, под влиянием потенциального, для простоты, стационарного поля с потенциалом 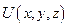, то определим функцию Лагранжа L следующим образом:

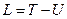,а действиемназовем величину:

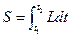. (4.1)

Покажем теперь, что экстремали функционала (1), т.е. те уравнения для 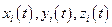, для которых функционал (1) приобретает экстремальное значение, описывают реальные траектории движения или, что то же самое, удовлетворяют динамическим уравнениям движения. Эти рассуждения близки к приведенным в приложении 2.6. Проведем их, в общем, чем для приведенного выше выражения, случае.

Пусть экстремаль для (1) существует и есть 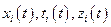, i=1,….N. Выберем для определенности функцию 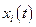и рассмотрим её вариацию 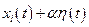, где α-некоторое число, 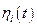- гладкая функция, обращающаяся в ноль на концах интервала 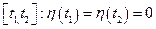. Последнее условие необходимо для того, чтобы варьируемая траектория при всех вариациях начиналась и заканчивалась в заданных точках. Поскольку 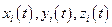есть экстремали, то действие:

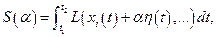
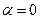как функция параметра , должна иметь экстремум при значении . Следовательно:

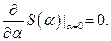
Считаем, что функция Лагранжа L содержит в качестве своих аргументов t, 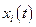и 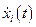. Тогда из условия:

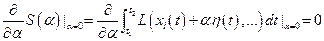
получаем:

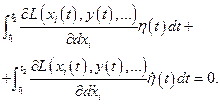
Далее:

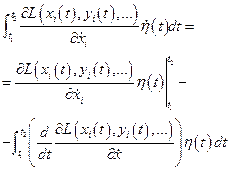
Первый член последнего выражения тождественно равен нулю в силу наложенных на функцию 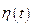условий. Тогда получаем:

.

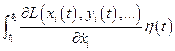
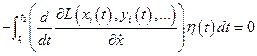Поскольку это требование должно быть выполнено для любой функции 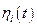, получаем следующее уравнение:

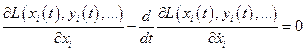. (4.2^а)

Повторяя приведенные рассуждения для функци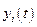й и 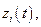получим ещё два уравнения:

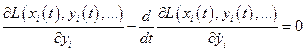. (4.2^б)

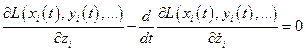. (4.2^в)

Система уравнений (2) называется системой уравнений Эйлерадля вариационной задачи:

.

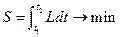Подставив в полученные уравнения Эйлера принятую для системы функцию Лагранжа

и учитывая равенства:

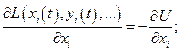
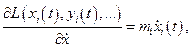
получим:

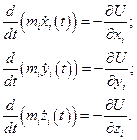(4.3)

Но, поскольку производная от потенциала – это минус соответствующая компоненте напряженности поля, получим, что последняя система уравнений – это в точности система уравнений Ньютона (второй закон Ньютона) для динамики системы точек. Таким образом, получено обоснование принципа наименьшего действия:

Величина 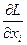имеет смысл компоненты в направлении оси ОХ силы, действующей на i-ую частицу, а 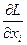- проекция на ось ОХ импульсаi-ой частицы: 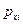. Тогда уравнение Эйлера дает следующий результат:

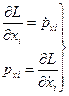(4.4^а)

Аналогично можно записать для компонент в направлении осей OY и OZ:

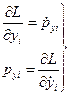(4^б)

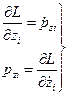(4^С)

Координаты и импульсы частицы с номером i будем обозначать x_i и p_i соответственно. Причем 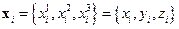, 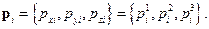Полный набор всех координат и импульсов будем обозначать одной буквой без индексов: x,pсоответственно.

Уравнение Эйлера, равно как и сама функция Лагранжа, записаны в переменных: координаты – x_i, скорости - 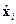. Импульсыp_i определены уравнениями (4).

Уравнения:

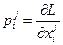
можно разрешить относительно скорости 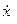, если матрица Гесса:

,

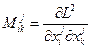неособенная для каждого j = 1, 2, 3. Последнее означает, что её определитель не равен нулю. В этом случае скорости 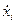можно выразить через координаты и импульсы так, что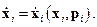

Определим функцию Гамильтонаследующим образом:

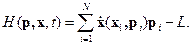
Здесь в функции Лагранжа также скорости выражены через импульсы. Вычислим вариацию 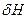функции Гамильтона.

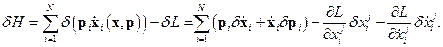
Но

,

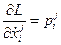и

.

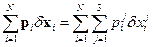В результате последний и первый член сокращаются. Тогда получаем:

,

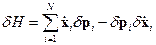откуда следует[46]

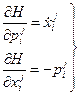. (4.5)

Система уравнений (5) представляет собой эквивалент уравнений движения Эйлера, но выраженных через функциюГамильтона. Эти уравнения называются гамильтоновой формой уравнений движения.

Функция Лагранжа представляет собой разность между кинетической и потенциальной энергиями: 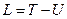. Поставляя в выражение для функции Гамильтона конкретные значения, входящих в нее компонент, и учитывая, что:

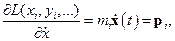
получим

.

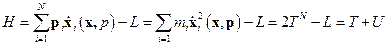Таким образом, функция Гамильтона представляет собой сумму кинетической и потенциальной энергий – полную энергию системы.

Переход от лагранжевой к гамильтоновой форме требует неособенности матрицы Гессе:

.

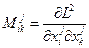Это условие может быть, вообще говоря, и не выполнено. Таким образом, указанный переход возможен не всегда.

Свойства системы и законы её развития не меняются, если переместить её как целое в другую точку пространства. Это значит, что функция Лагранжа не меняется при преобразованиях координат типа сдвига: 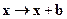, и вариация лагранжевой функции при вариации координат равна нулю:

.

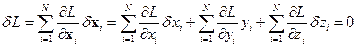Поскольку 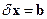, и это произвольный вектор, то:

.

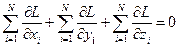Учитывая уравнение Эйлера, получим:

.

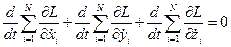Но последнее выражение представляет собой закон сохранения импульса:

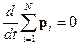
Таким образом, из однородности пространства следует сохранение во времени импульса системы. Это утверждение можно обратить, сказав, что импульс – это то, закон сохранения для чего вытекает из однородности пространства.

Предположим, что лагранжева функция не зависит явно от времени. Тогда 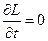, т.е. время однородно.

Полная производная по времени от лагранжевой функции равно:

.

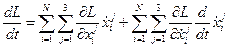Принимая во внимание уравнения Эйлера:

,

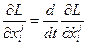последнее равенство можно переписать:

.

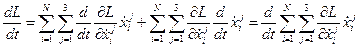Окончательно

,

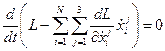Или

.

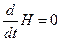Таким образом, однородность по времени влечет за собой закон сохранения полной энергии системы. Это утверждение можно также обратить, приняв, что энергия системы – это то, закон сохранениячего вытекает из однородности времени.

Приведенный способ описания движения через стационарное значение действия можно распространить на описание физических полей. При этом возникают особенности. Переход от системы из N материальных точек к непрерывно распределенному в пространстве физическому полю означает замену конечномерного случая бесконечномерным. Для вычисления энергетических характеристик поля в заданной пространственно-временной области в таком случае следует осуществлять интегрирование по этой области. Тогда то, что оказывается под знаком интеграла, естественно назвать не функцией Лагранжа, а лагранжевой плотностью.

Проиллюстрируем это примерами:

Пусть скалярное стационарное поле 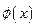, 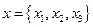распределено в пространстве таким образом, что для любой области 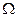действие:

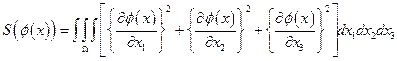(4.6)

стационарно.

Лагранжевой плотностьюявляется функция

,

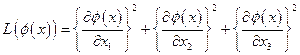а сформулированный принцип наименьшего действия можно записать:

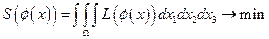
Действительно, рассмотрим вариацию поля 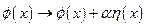, где - некоторой числовой параметр, а 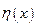- гладкая функция, обращающаяся в ноль на границе 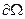области 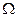. Стационарность действия при реальном распределении поля означает, что:

.

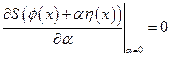Тогда получаем:

,

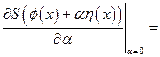
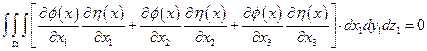где .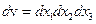

Далее, поскольку:

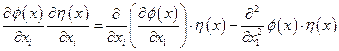, получим:

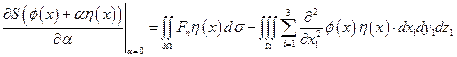
Здесь 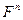- компонента в направлении нормали к поверхности 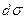, ограничивающей область 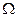, вектора 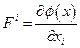. Поскольку 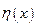равно нулю на границе области 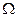, то первый член в правой части последнего равенства равен нулю, а поскольку область была произвольной, то стационарность действия означает равенство нулю подынтегрального выражения во втором члене правой части. Тогда получаем, что стационарность действия (6) означает, что рассматриваемое поле удовлетворяет уравнению:

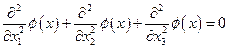. (4.7)

Но (7) – это в точности уравнение Лапласа. Таким образом, поле, удовлетворяющее уравнению Лапласа, соответствует принципу наименьшего действия, где действие имеет вид (6).

Рассмотрим теперь нестационарное пол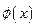е , где 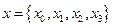, и потребуем стационарности действия:

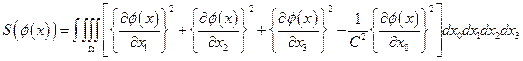(4.8)

Здесь 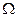- четырехмерная область в пространственно-временном многообразии. Лагранжевой плотностьюявляется функция:

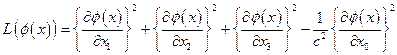
Повторяя приведенные выше рассуждения, легко получить, что стационарность так построенного действия эквивалентна выполнению для поля 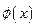уравнения:

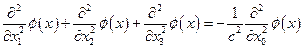(4.9)

Это известное в математической физике волновое уравнение, которое описывает процесс распространения волны в однородной среде со скоростью с. Таким образом, принцип стационарного действия (8) приводит к выводу о том, что удовлетворяющее ему поле удовлетворяет волновому уравнению.