Краткие теоретические сведения. В современном физическом эксперименте все чаще применяется сложная радиотехническая

2.1. Введение.

В современном физическом эксперименте все чаще применяется сложная радиотехническая аппаратура, измерения выполняются с высокой степенью точности, а количество информации, подлежащее обработке, значительно. В связи с этим возникает необходимость в преобразовании выходного сигнала в цифровую форму и в обработке его на быстродействующей ЭВМ, которая нередко является частью экспериментальной установки. Переход к интегральным микросхемам существенно изменил способы построения электронной аппаратуры, поскольку изделия микросхемотехники представляют собой законченные функциональные узлы.

В данной работе изложены основы булевой алгебры, принципы конструирования логических цепей на интегральных микросхемах и практические рекомендации по построению этих цепей и осуществлению в них соответствующих логических операций.

По выполняемым элементарным функциям интегральные схемы делятся на две большие группы: цифровые (логические) и аналоговые. Мы рассмотрим только первую группу. Этиинтегральные схемы предназначены для реализации логических функций и обработки информации, представленной в цифровом виде. Логические интегральные схемыхарактеризуются конечным числом состояний схемы,что определяется конечным числом уровней напряжений, действующих в схеме. Обычно напряжение может принимать только два значения: высокий уровень — условное обозначение «1» инизкий уровень — «0». В соответствии с этим для анализа и синтеза этих схем используется математический аппарат, связанный с функциями и переменными, принимающими только два значения, и называемый алгеброй логики или булевой алгеброй с соответствующими функциями и переменными.

2.2. Булевы функции.

Наиболее простые булевы функции — это функции одного аргумента.Таких функций существует четыре (табл. I). Черта над переменной или функцией обозначает ихинверсию (отрицание).

Булевы функции одного аргумента. Таблица I

	Значение аргумента X	Формулы функций F=…	Названия функций F
Значения функций			X	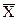Константа 0 Переменная X Отрицание X Константа 1

Отрицание (функция НЕ) может быть реализовано при помощи фазоинверторов, причем под изменением фазы здесь понимают замену высокого уровня входного напряжения «1» на низкий «0» и наоборот. В простейшем случае ее можно осуществить с помощью контакта, параллельного нагрузке (рис. 1).

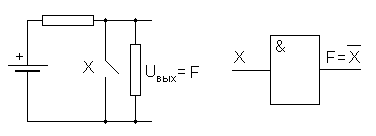
Рис. 1. Реализация функции НЕ и ее обозначение:

разомкнутый контакт соответствует Х=О, замкнутый — Х=1

Важнейшие булевы функции двух аргументов Таблица 2

	Значение аргументов	Формулы функций F=…	Названия функций F
X1
X2
Значения функций					X1×X2 X1+ X2	Логическое “И” Логическое “ИЛИ”
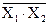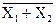					Отрицание “И” Отрицание “ИЛИ”
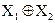				X1~ X2	Сумма по модулю 2 Эквивалентность
				X1 X2	Переменные X1 Переменные X2
					Отрицание X1 Отрицание X2
					Константа 0 Константа 1

Константы «0», «1» и переменная «Х» могут быть осуществлены непосредственным соединением нагрузки с источником низкого уровня напряжения, высокого уровня и с источником сигнала «Х» соответственно.

Булевы функции двух аргументов приведены в табл. 2. Функция «И» принимает значение, равное 1, тогда, когда оба ее аргумента равны 1. Говорят, что данная функция выполняет логическое перемножение переменных. Данную функцию выполняют обычная схема совпадений или последовательно соединенные пары контактов (рис. 2). Функция «ИЛИ» принимает значение, равное 1, тогда, когда хотя бы один ее аргумент равен 1. Говорят, что эта функция выполняет логическое сложение переменных. Данную функцию выполняет схема сложения сигналов, например, параллельно соединенные пары контактов (рис. З).

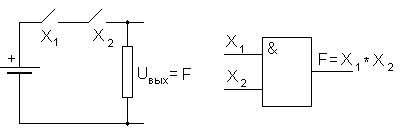
Рис. 2. Функция «И»

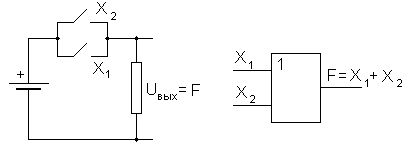
Рис. 3. Функция «ИЛИ»

Свойства остальных функций ясны из их названий и формул. Ниже приведены основные аксиомы логической алгебры. Их непротиворечивость может быть легко проверена путем подстановки в обе части равенств переменных 1 и 0.

1) — закон двойного отрицания;

2) X₁×X₂= X₂×X₁ и X₁+X₂= X₂+X₁ — переместительные законы (коммутативности);

3) X₁×(X₂×X₃)=(X₁×X₂)×X₃ и X₁+(X₂+X₃)=(X₁+X₂)+X₃ — сочетательные законы (ассоциативности);

4) X₁×(X₂+X₃)=X₁×X₂+X₁×X₃ и X₁+(X₂×X₃)=(X₁+X₂)(X₁+X₃)— распределительный закон (дистрибутивности);

5) X×X=X и X+X=X — законы тавтологии;

6) )X₁×(X₁+X₂)=X₁ и X₁+(X₁×X₂)=X₁ — законы поглощения;

7) 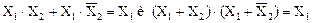— законы склеивания;

8) 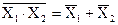и — законы инверсии (де Моргана);

9) 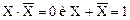=0 — законы дополнительности.

Многие законы, например, переместительный, сочетательный, распределительный, инверсии, можно распространить наслучай большого количества переменных. Для этого достаточно в эти законы вместо одной из переменных подставить комбинацию (суперпозицию) нескольких других переменных. Таким же образом, подставляя вместо аргументов булевой функции какие-либо другие булевы функции или их комбинации, можно получить бесчисленное множество различных сложных функций. Возникает вопрос: возможен ли набор более простых булевых функций, на основании которых можно получить любую, сколь угодно сложную? Такой набор называется полной системой. Оказывается, полных систем существует много. Почти очевидная система состоит из 3 основных функций: И, ИЛИ, НЕ. Менее очевидно, что существуют системы, состоящие только из одной функции. Например, такими функциями являются ИЛИ-НЕ и И-НЕ (рис. 4).

Докажем функциональную полноту функции И-НЕ, для чего рассмотрим получение из нее функций И, ИЛИ, НЕ:

а) операция НЕ получится, если в качестве аргументов функции И-НЕ взять X и 1: ;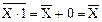

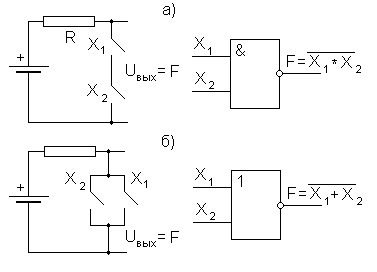
Рис. 4. Функции:

а)— И-НЕ;б)— ИЛИ-НЕ

б) операция ИЛИ получится, если в качестве аргументов взять функции , а операцию НЕ мыуже умеем делать: 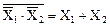(закон инверсии + двойное отрицание);

в)операция И получится, если взять отрицание функции И-НЕ.

Аналогично можно доказать функциональную полноту функции ИЛИ-НЕ.

Тот факт, что полная система может быть образована только из одной функции, является исключительно важным напрактике, т. к. на основе однотипных (базовых) микросхем можно получить любую, сколь угодно сложную функцию любого числа переменных. Для построения таких комбинационных схем необходимо, чтобы выходы базовых микросхем можно было подключать к входам других таких схем. Число возможных входов, обеспечивающихся одним выводом базовой микросхемы, определяет функциональные возможности микросхемы и называется коэффициентом размножения по выходу.

2.3. Реализация сложных логических функций на интегральных микросхемах.

Учитывая ограниченный ассортимент (набор) интегральных схемпо числу выполняемых операций, для практической реализации произвольных логических функций часто необходимо представить их через единственную операцию типа И-НЕ или ИЛИ-НЕ. Такое преобразование выполняется в 3 этапа.

2.4.Составление функционального уравнения.

На этом этапе выписывают те комбинации значений переменных, при которых искомая функция — «ИСТИНА», т. е. равна 1, далее каждую комбинацию записывают в виде произведения тех переменных, которые в данной комбинации равны 1, а затем все полученные произведения суммируют. Пусть, например, требуется сконструировать «пороговую» ячейку для трех сигналов, на выходе которой напряжение равно единице только в том случае, когда, по крайней мере, два сигнала равны 1. Обозначив переменные буквами X₁,X₂, а функцию — F, видим, что F=1 в том случает, если X₁=1, X₂=1, X₃=1, или X₁=1, X₂=1, X₃=0, или X₁=1, X₂=0, X₃=1, или X₁=0, X₂=1, X₃=1. Данное условие можно записать в виде:

.

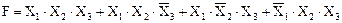Для отыскания всех возможных комбинаций переменных, обеспечивающих единичное значение функции, используют таблицы состояний (рис. 5).

			X1				X2X1
X2
				X4X3

				X2X1
X3

Рис. 5. Таблицы состояний простых произведений:

а — для двух, б — трех и в — четырех переменных

Вместо нулей и единиц в таблице можно указывать десятичные эквиваленты двоичных чисел, соответствующих наборам переменных (рис. 6). Например, двоичное число 1010 в десятичной системе будет равно:

1×2³+0×2²+1×2¹+0×2⁰=10.

X2X1			X2X1
				X3

		X2X1
X4X3

Рис. 6. Таблицы состояний, выраженные десятичными цифрами

Процедура составления функционального уравнения заключается в переборе всех клеток таблицы состояний и занесении единиц в клетки, которые определяют логическое произведение переменных, дающее истинное значение функции F. В частности, для нашего случая будем иметь F(3,5,7,6)=1 (рис. 7).

Рис. 7. Диаграмма минимизации функции F

2.5. Преобразование полученного уравнения с целью возможного упрощения.

Для преобразования можно использовать как непосредственно аксиомы алгебры логики, так и специальные приемы. Произведем упрощение выражения для F на основе аксиом.

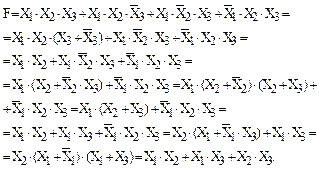
Другим, более простым, способом получения минимизированного выражения является построение диаграмм минимизации для чего в таблице состояния единицы обводятся контурами, содержащими 2, 4 или более (число, кратное 2) клеток. Контуры могут перекрываться.

Для нашего случая можно построить три таких контура, содержащих по две клетки. Искомое минимизированное выражение есть логическая сумма укороченных произведений переменных, имеющих одно значение в пределах контура, без переменных, имеющих оба возможных значения (0 и 1) в пределах контура. Таким образом, согласно рис. 7, будем иметь

,

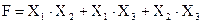где первый член дает вертикальный контур, второй член — правый горизонтальный контур и третий член определяется левым горизонтальным контуром.

2.6.Дальнейшее преобразование уравнения с целью приведения его к виду, реализуемому данными интегральными схемами.

Пусть, например, мы имеем только схемы, выполняющие операции И, НЕ. Тогда предыдущее выражение приводится к следующей форме:

_.

После этого можно уже рисовать функциональную схему, выполняющую операцию F (рис. 8).

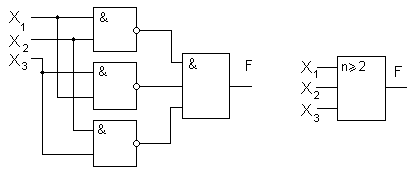
Рис. 8 Рис. 9

Для этого устройства на функциональных схемах принято обозначение, изображенное на рис. 9. Интересно отметить, что данная схема находит практическое применение в устройствах передачи информации для выделения сигнала из помех. По Nнезависимым каналам передается один и тот же сигнал (например, единица). В процессе передачи из-за различных помех единица с некоторой вероятностью Р может стать нулем. Если считать единицей момент, когда единица передана большинством каналов (например, хотя бы двумя из трех), то вероятность ошибки будет 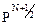. В частном случае трех каналов N=3 и P=5% (0,05) будем иметь Р_S=0,25% (0,0025), т. е. вероятность ошибки существенно уменьшается. Данная схема также используется при поразрядном сложении чисел в двоичной системе для определения переноса в следующий разряд. Перенос в следующий разряд будет равен единице, если, по крайней мере, два числа из трех (два слагаемых и перенос из предыдущего разряда) равны единице.

Рассмотрим другую логическую схему, называемую полусумматором. Она применяется при поразрядном сложении чисел в двоичной системе и определяет сумму, оставшуюся в данном разряде. Сумма будет равна единице только тогда, когда лишь одна переменная равна единице. Если обе переменные равны единице, сумма будет равна нулю, а единица переносится в следующий разряд. Этот перенос с учетом переноса из предыдущего разряда, как уже упоминалось, осуществляется операцией n ³2 (рис. 9).

Для суммы можно записать условие F(1,2)=1 (рис. 10).

Рис. 10. Таблица состояний функции F(1,2) = 1

Как видно из таблицы состояний, функцию F можно записать в следующем виде 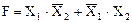. Структурная схема данной логической операции показана на рис. 11.

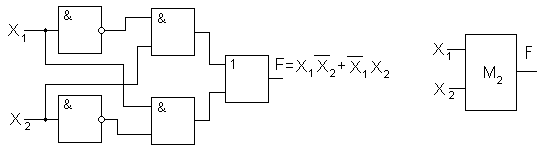
Рис. 11 Рис.12

Общая схема полусумматора представлена на рис. 12 (М₂ обозначает сложение по модулю 2).

Схема полного сумматора с учетом переноса из предыдущего в последующие разряды показана на рис. 13. Ее обозначение приведено на рис. 14.

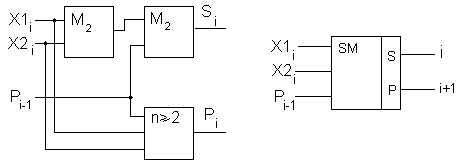
Рис. 13 Рис. 14

Конкретная реализация сумматора может быть различной в зависимости от наличия интегральных схем,выполняющих те или иные логические функции. Есть сумматоры, полностью изготовленные на одной микросхеме. Количество таких сумматоров должно быть равно числу двоичных разрядов складываемых чисел.

2.7. Триггеры.

Триггер — логическое устройство, состояние которого зависит не только от приложенных в данное время сигналов, но и от состояния триггера в предшествующий момент времени. Широко применяются так называемые тактируемые (синхронизируемые) триггеры с дополнительным входом, так что если на этом входе 0 — состояние триггера не меняется, если 1 — производятся операции. Ниже приведена таблица состояний наиболее употребляемых триггеров (табл. 3).

Состояния наиболее употребляемых триггеров Таблица 3

Состояние входов	Состояние триггера Qn
X1	X2
		Qn-1	Qn-1	Qn-1	Qn-1	Qn-1
		Xнеопр.	Qn-1			Qn-1
		RS	JK	R	S	E

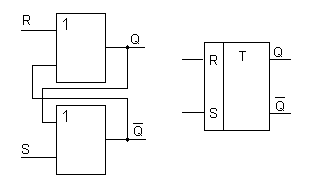
Рис. 15. Реализация RS-триггера и его обозначения

Существуют триггеры с одним переключающим входом (триггер D), но с обязательным тактирующим входом. При подаче на тактирующий вход единицы производится операция: если на переключающем входе 1 — на выходе будет единица, если на входе 0 — на выходе 0.

Реализация RS-триггера на элементах ИЛИ-НЕ приведена рис. 15.

Входы триггеров принято обозначать теми же буквами, которые использованы в его названии. RS-триггер обладает следующими свойствами:

1) сохраняет состояние при S=R= 0 ;

2) устанавливается в «1» при S=1, R=0;

3) устанавливается в «0» при S= 0, R = 1;

4) комбинация S = R=1 запрещена, т.к. в этом случае состояние триггера неопределенное (Q=x).

RS-триггер, кроме использования его как элемента в различных логических операциях, может также применяться как быстродействующий «бездребезговый» переключатель. При этом «дребезг» на входе триггера (поочередное соединение и разъединение контакта) не передается на выход. Триггер опрокидывается (переключается) при первом касании, а дальнейшие смены состояний одного входа при нулевом втором входе не приводят к смене состояния триггера.

Триггеры JК,R, S, Е, как видно из таблицы, различаются только состояниями, которые они принимают при единичных уровнях на обоих входах. Из них наиболее часто применяется триггер JK, который при единичных обоих входах меняет свое состояние на противоположное.

Триггеры в основном используются в схемахдвух типов: регистрах и счетчиках.

2.8. Регистры.

Регистры — это устройства для приема, хранения и передачи информации, причем информация здесь — это некоторое сочетание нулей иединиц. Кроме того, на регистрах выполняются некоторые операции над числами. В качестве простейшего регистра может быть использован тактируемый триггер RS. На вход, например, R, поступает один разряд информации (один разряд двоичного числа), который надо запомнить; на вход S подается инверсия этого разряда, т. е. S= 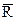. Тогда с приходом тактирующего импульса триггер устанавливается в соответствующее состоявшие и в дальнейшем сохраняет его независимо от состояния входов Rи S до прихода следующего тактирующего импульса. Информация может быть снята с выходов 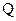и 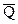, т. е. уровень напряжения на выходах говорит о том, какие потенциалы были на входе в момент прихода тактирующего импульса. Аналогично работает такой регистр на триггере Q. Соединяя несколько триггеров-регистров параллельно (по тактируемому входу), можно запомнить многоразрядные двоичные числа и получить так называемый параллельный регистр, характеризуемый одновременной записью всех разрядов. Пример последовательного регистра (регистр сдвига) представлен на рис. 16.

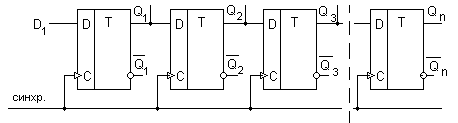
Рис. 16. Последовательный регистр на триггерах D:

С — тактируемые входы триггеров

Информация поразрядно поступает на вход D₁. Будем обозначать состояние m-го триггера после прихода n-го тактирующего импульса 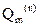. С приходом тактирующего импульса (после поступления информации) первый триггер устанавливается в состояние 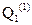, соответствующее первому разряду (обозначим его ) числа. Затем на вход D₁ поступает второй разряд 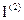, а на С - следующий тактирующий импульс.

В результате второй триггер устанавливается в состояние, в котором до этого был первый: 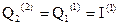, а в первом триггере запишется информация о втором разряде 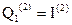и т. д., т. е. последовательно слева направо происходят запись и сдвиг разрядов информации. После поступления n-тактовых импульсов в регистре запишется n-разрядное число и с выходов оно может быть снято, как и в параллельном регистре, т. е. одновременно по всем разрядам. Если тактирующие импульсы продолжать подавать на входы С, то с выхода информация может быть снята уже в виде последовательного кода. При этом информация, хранящаяся в регистре, стирается. Имеются микросхемы,полностью выполняющие функции многоразрядного регистра.

2.9. Счетчики.

Счетчиком называется устройство, имеющее N устойчивых состояний, которые последовательно переходят одно в другое при поступлении входных сигналов (импульсов). Таким образом, состояние счетчика позволяет судить о том, сколько импульсов поступило на вход. Такие устройства широко применяются, например, в ядерной физике. Второе применение счетчиков — деление частоты. Пусть у счетчика имеется N устойчивых состояний, при поступлении на вход счетчика последовательности импульсовсчетчик будет последовательно переходить из одного состояния в другое. Через каждые Nимпульсов определенное состояние счетчика будет повторяться. Таким образом, частота повторения того или иного состояния счетчика будет в N раз меньше частоты входных импульсов, т. е. мы получим N-кратное деление частоты. Структурная схема счетчика показана на рис. 17.

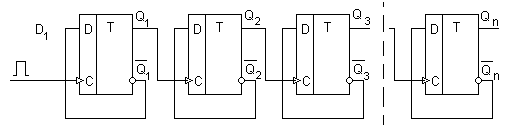
Рис. 17. Счетчик натактируемых D-триггерах