Приложение 2. Функциональный анализ. Линейные операторы. Экстремальные задачи (вводный конспект)

Этот раздел служит, в определенной мере, продолжением предыдущего и его обобщением на случай произвольных, в том числе, и бесконечномерных пространств. Все здесь сказанное имеет свою «проекцию» на конечномерный случай. В свою очередь, конечномерный случай можно рассматривать, в том числе, и как подготовительный материал к настоящему разделу, хотя он и содержит много самостоятельно интересных фактов. Множества, рассматриваемые здесь, служат обобщением координатных пространств, линейные операторы – матриц. Однако не каждый результат в конечномерном случае имеет свой очевидный аналог в бесконечномерном. Бесконечномерный случай содержит много нового и это новое необходимо, прежде всего, для понимания истинной сути и причины тех проблем, которые возникают при анализе «конечномерными методами» реальных геофизических полей. Любое интегральное уравнение можно представить в виде его конечномерного аналога. Это можно сделать многими разными способами. Но для того, чтобы увидеть общие свойства этих конечномерных моделей и сложности, возникающие с их использованием в процессе реконструкции физических моделей среды, конечномерных представлений недостаточно.

Множества.

Множествапредставляют собой исходный объект, на котором строятся те, либо иные, математические конструкции. Это одно из наиболее общих понятий, не поддающихся определению. Например, можно говорить о множестве всех натуральных чисел, множестве возможных геологических структур, литологических, либо стратиграфических разностей горных пород.

Множества обозначаются заглавными буквами А, B, C… Элементы множеств, как правило, обозначаются соответствующими малыми: а,b,c… . Иногда эти малые буквы снабжены индексами i, j, k, …, которые могут иметь значения из некоторое другого множества, например, множества натуральных чисел.

Тем самым осуществляется идентификация конкретных элементов множества. Иногда множество, состоящее из элементов 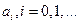, обозначается (а).

Прежде всего, договоримся об использовании обозначений, часть из которых использовалась и ранее.

1) - пустое множество;

2) а 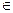А - элемент а принадлежит множеству А;

3) - элемент а не принадлежит множеству А;

4) 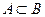- множество А есть подмножество в В;

5) 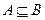– то же, что и 4, но возможно равенство А и B;

6) 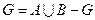есть объединение (сумма) А и В, т.е. состоит из элементов, принадлежащих А, либо В;

7) G= A / B – G есть дополнение В до А, т.е. состоит из элементов в А, не принадлежащих В;

8) 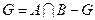есть пересечение (произведение) А и В - т.е. состоит из элементов, одновременно принадлежащих А и В.

Далее используются кванторы всеобщности и существования 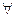и .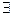

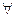- квантор всеобщности. Например, предложение

читается так: справедливо утверждение 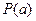(здесь вместо 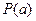может быть любое выражение) для любого элемента а из множества А. Или:

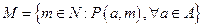
М - есть множество элементов из N, для которых справедливо предложение 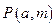при любом а из А.

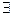–квантор существования. Предложение « 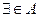» читается так:

существует элемент (найдется элемент) а из А.

Выражением 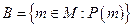определяется множество В: В есть совокупность элементов m из М таких, что выполнено предложение .

Приведенные символические записи используются для сокращенной формулировки тех либо иных предложений.

Совокупность всех подмножеств множества А обозначается . Это новое множество. Его элементами, служат, например, все А и каждый из элементов в отдельности. Между двумя множествами можно построить отображение.

Будем говорить, что задано отображение f из А в В, (записывается в виде 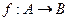), если некоторым элементам из поставлены в соответствии некоторые элементы из .

В приложениях теории множеств удобно пользоваться принципом двойственности, который основан на следующих соотношениях.

Если последовательность множеств, занумерованная индексом i, и S – множество, содержащее все , то:

1) 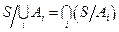(дополнение суммы множеств равно пересечению их дополнений);

2) (дополнение пересечений равно сумме дополнений).

Предлагаем читателю нарисовать рисунки и самостоятельно доказать этот результат.

Благодаря принципу двойственности, из любой теоремы, относящейся к системе подмножеств фиксированного множества S, автоматически получаются новые теоремы, в которых множества заменены их дополнениями, объединение – пересечениями, пересечения – объединениями.

Множество А называется частично упорядоченным, если для некоторых его элементов а_i установлено отношение: либо 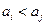, либо , либо 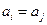. Это отношение удовлетворяет условиям:

1) 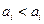либо при любом ;

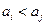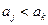2) если и , то ;

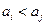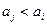3) если и , то .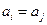

Символы “<” и «=» нельзя понимать только в узком смысле – меньше, равно. Их значение шире - упорядочение либо эквивалентность по любому признаку.

Множество называется упорядоченным(или вполнеупорядоченным), если отношение порядка установлено для любых двух элементов из А.

Пример частично упорядоченного множества - множество комплексных чисел, где в качестве отношения порядка установлено сравнение их вещественных и мнимых чисел. Пример вполне упорядоченного множества - множество вещественных чисел.

Другой нетривиальный пример частичного упорядоченного множества, который используется, таков. Предположим, что некоторая площадь находится на этапе разведки. Имеющиеся сведения о геологическом строении района еще не позволяют однозначно вырисовывать тип геологической структуры. Тем самым допускается множество А возможных структур. Однако, каждая из них соответствует в большей, либо в меньшей, степени имеющимся сведениям о районе - реально имеющимся данным. Тогда для некоторых различных структур можно указать, какая из них более, а какая менее соответствует имеющимся данным. Благодаря этому на множестве А вводится структура частичного упорядочения. Если такое сравнение можно сделать для любых двух элементов из А, то введенная структура упорядочения является вполне упорядоченной. Интуитивно представляется очевидным, что возможность введения структуры вполне упорядоченного множества из А соответствует большей изученности теории.

2.2. Топология*.

Определенное выше понятие отображения является столь общим, что лишено какого-либо конструктивного начала. Для того чтобы отображение обладало свойствами непрерывности, либо, наоборот, не обладало ими на множествах, которые ставит отображение в соответствие друг другу, должна быть определена соответствующая структура, позволяющая определить понятие непрерывности. Такой структурой служит топология.

Топологическое пространство– это множество А с выделенным в нем семейством подмножеств τ, называемых открытыми, и обладающее следующими свойствами:

1)

2) пересечение конечного числа элементов из τ есть снова элемент из τ;

3) объединение любого семейства элементов из τ есть снова элемент из τ;

Система τ называется топологией пространства А, и все топологическое пространство обозначается (А, τ). Когда топология определена и путаница исключена (из текста ясно, о какой топологии идет речь), используется просто запись .

Одно и тоже множество А может быть снабжено несколькими различными топологиями. Такая ситуация распространена.

Топология 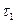слабее топологии 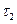( 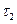сильнее 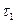), (обозначается ), если каждое множество из τ₁ одновременно принадлежит τ₂. Иными словами, в 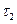есть все элементы из 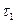плюс, возможно, и многое другое. Более сильная топология это та, которая содержит все открытые подмножества, входящие в состав более слабой и, кроме того, содержит еще множества, возможно более мелкие, позволяющие увидеть более тонкие эффекты, которых (множеств) нет в более слабой топологии.

Пусть А есть множество, τ – выделенная в нем топология, В - подмножество в А. Обозначим 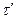- совокупность множеств, полученных как пересечение В и элементов из τ. Если (В, 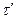) топологическое пространство, то 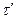называется индуцированной топологией на В и (В, 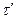) подпространством в (А, τ).

Базой γ топологииτ называется такое подмножество в τ, что любые элементы из τ могут быть получены с помощью операций объединения любого числа и пересечения конечного числа (относится только к пересечению) элементов из γ.

Дополнение к элементам из τ называются замкнутыми множествами.

Замечание. Множество может быть одновременно открытым и замкнутым - это все А и пустое множество - . Множество, не являющееся открытым, может и не быть замкнутым, т.к. не всякое множество есть дополнение к открытому.

Наименьшее замкнутое множество в топологическом пространстве (А, τ), содержащее заданное множество В, называется замыканиемВ и обозначается 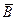. Если 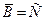, то говорят, что В плотно в С в топологии τ.

Множество В топологического пространства (А, τ) называется нигде не плотныммножеством, если оно не плотно ни в одном из закрытых множеств в ( А, τ).

Множество, полученное объединением не более чем счетного числа нигде не плотных множеств, называется множеством первой категории. Дополнение к множеству первой категории есть множество второй категории.

Множество, полученное в результате замыкания, зависит от используемой топологии. Если (А, τ₁) и (А, τ₂) - два топологических пространства над одним и тем же множеством А, и топология τ₁ слабее топологии τ₂ (τ₁ < τ₂), то замыкание В₁ множества В в топологии τ₁ содержит в себе замыкание В₂ того же множества в топологии τ₂: В₂ 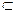В₁ .

Окрестностью точки называется произвольный элемент из τ, содержащий эту точку а. Окрестностью замкнутого множества называется открытое множество, включающее в себя это замкнутое.

Топологическое пространство называется хаусдорфовым, если любые две его точки имеют непересекающиеся окрестности.

Топологическое пространство называется нормальным или отделимым, если в нем всякие два непересекающиеся замкнутые множества имеют непересекающиеся окрестности.

Теорема 1.Пересечение любого числа и сумма любого конечного числа замкнутых множеств есть замкнутое множество.

Для доказательства к определению понятия топологии следует применить принцип двойственности. Тогда, поскольку замкнутые множества есть дополнение к открытым, заменив в определении открытые множества замкнутыми, объединения - на пересечения и, наоборот, получим утверждение теоремы.

Точка а называется внутренней точкой множества А, если существует окрестность этой точки, целиком лежащая в А. Все точки открытого множества – внутренние. Множество первой категории не имеет внутренних точек. Но замыкание множества первой категории может иметь внутренние точки.

Эквивалентным понятию отображение является понятие функции.

Задать отображение из множества А во множество В – значит определить закон, согласно которому элементу ставится в соответствие элемент 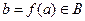. Этот закон может быть определен не для всех элементов из . Совокупность тех элементов из А, для которых этот закон определен, называется областью определенияотображения f и обозначается D(f).

Совокупность элементов из b, являющихся образом элементов из 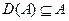при отображении f, называется множеством значений отображения f и обозначается .

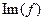Отображение называется однозначным, если элементу а соответствует только один элемент из В, являющейся образом а.

Наряду с отображением f как законом преобразования из в 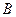, вводится ему обратное следующим образом: . Если отображения f и одновременно однозначны, то f - взаимнооднозначное отображение. Точка , если она существует, называется прообразомточки b при отображении f.

Введенное понятие отображения соответствует использованному раннее как закону, который элементам из ставит в соответствие элемент из . Действительно, если N – некоторое подмножество в А, то его образ при отображении f обозначим 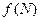. Этот образ есть подмножество в В.

Благодаря введению топологии, для отображения может быть определено понятие непрерывности.

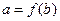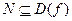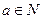Отображение непрерывно в точке , если, каково бы ни было множество N, из и следует .

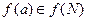f - непрерывное преобразованиена А, если оно непрерывно во всех точках множества А. Эквивалентное определение непрерывности, явно использующее понятие топологии, таково: f непрерывно, если во всякой окрестности точки 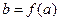существует окрестность 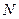точки и .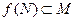

Следующие необходимые и достаточные условия непрерывности отображения f в каждой точке множества эквивалентны.

.

1) прообраз любого открытого множества 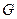есть множество открытое;

2) прообраз 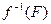любого замкнутого множества 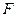есть множество замкнутое;

3) если , то

4) если 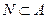, то .

Если отображения f и одновременно непрерывны, то f называется взаимно- непрерывным отображением.

Взаимно-непрерывное и взаимнооднозначное отображение называется гомеоморфизмом. Это очень важное понятие.

Говоря о непрерывности отображения, следует уточнить область определения и топологию, в которой это отображение непрерывно. Одно и тоже отображение может быть непрерывным в одной топологии и оказаться разрывным в другой.

Объекты, которые рассматриваются в функциональном анализе и его приложениях, помимо топологической, наделены и алгебраической структурой.

Бинарной операциейназывается операция, которая каждым двум элементам ставит в соответствие третий элемент.

Для дальнейшего достаточно использовать три типа операций, которые условимся называть сложением, умножением (внутренним умножением) и умножением на вещественные либо комплексные числа. Другие эквивалентные названия этих операций - аддитивная, мультипликативная и умножение. Выбранное множество может быть снабжено одной из этих операций, двумя либо тремя. В зависимости от этого получаются те либо иные алгебраические структуры. Множества, наделенные алгебраическими операциями, это уже нечто совсем иное, чем обычные множества. Для них будем использовать более привычные обозначения .

Пусть Х - множество, содержащее, по крайней мере, два различных элемента, в котором определена бинарная операция, называемая сложением. Ее обозначаем «+». Х называется аддитивной группой, если выполняются следующие условия:

1) всякая пара (x,y) из X имеет единственный элемент ;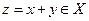

2) существует элемент 0 и ;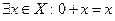

3) для всякого элемента х существует элемент -х и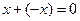

Группа называется коммутативной или абелевой, если сложение коммутативно:

Если Х есть аддитивная группа и топологическое пространство одновременно, то Х называется топологической аддитивной группой, если аддитивная операция непрерывна топологии пространства Х относительно каждого из двух участвующих в операции элементов. Иными словами – сложение непрерывно.

В аддитивную группу вводится другая операция - умножение на скаляры. В качестве скаляров выступает либо множество комплексных чисел, которое будем обозначать , либо множество вещественных чисел- R.

Коммутативная абелева группа X называется линейной системой(модулем) над скалярным множеством (R либо ), если на ней однозначно определена операция умножения на скалярные числа α:

1) ;

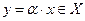2) ;

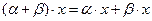3) ;

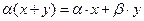4) ;

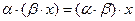5) .

Линейную систему называют также линейным векторным пространством, а ее элементы - векторами. Это название не отражает истинного смысла понятия вектор в векторном анализе и не следует путать с ним. Об этом говорилось в приложении 1.

Линейная система, содержащаяся в некоторой другой линейной системе, называется ее линейным подпространством. Для любого множества Y, содержащегося в линейном векторном пространстве Х, существует наименьшее линейное векторное подпространство в Х, содержащее Y. Оно состоит из элементов 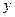вида:

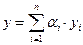
где , 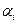- скаляры.

Подмножество С линейной системы Х называется выпуклым,если из условий следует, что и каждая их выпуклая комбинация , содержится в С.

Для всякого множества С существует наименьшее выпуклое множество С_0, содержащее С. Оно состоит из всех векторов 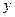вида:

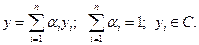
n - конечное число.

Множество С₀ называется выпуклой оболочкой множестваС.

Предположим, что Х₁, Х₂,…,Х_n - линейные системы над одним и тем же множеством скаляров. Произведением, или прямой суммой Хⁿ, множеств Х_i , i=1,2,.. n, называется множество всевозможных упорядоченных систем ( ), в которых 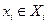. Такое произведение обозначается Арифметические операции в нем определены покомпонентно равенством:

Топологическое линейное пространство (линейное пространство) - это линейная система, являющаяся топологической аддитивной группой, в которой определена операция умножения на скаляр, являющаяся непрерывной функцией от (α, х).

Топологическое линейное пространство называется локально выпуклым, если оно обладает базисом, состоящим из выпуклых окрестностей. В топологическом линейном пространстве можно ввести понятие сильной выпуклости. Множество С называется Сильно выпуклым, если оно выпукло, и для любых двух точек все точки прямой , имеют окрестность, целиком лежащую в С.

Если линейное пространство Х содержит подмножество Y само являющееся линейным пространством, то Y называется линейным подпространствомв Х. Если Y – дополнительно замкнутое множество, то Y – замкнутое подпространство.

Наряду со сложением и умножением на скаляр в топологическом линейном пространстве может быть введена операция умножения двух элементов - мультипликативная операция. Она может рассматриваться и независимо от введенных выше, и в этом последнем случае возникает объект, называемый группой, либо группоидом, в зависимости от того, все ли эти элементы имеют обратные. Однако столь общие объекты далее использоваться не будут, поэтому мультипликативная операция вводится как дополнение к уже введенным – на топологическом линейном пространстве.

Линейная система называется алгеброй, если в ней существует мультипликативная операция, называемая умножением, а результат ее действия - произведение, удовлетворяет условиям:

1) для всякой пары элементов 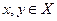однозначно определено их произведение ;

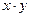2)

3)

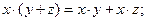
4)

Если в алгебре существует элемент «е» такой, что 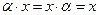для любого 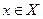, то она называется алгебра с единицей. Если , то алгебра называется коммутативной.

Алгебра Х называется топологической алгеброй (топологическим алгебраическим пространством), если Х - топологическое пространство, и для любых х, y в окрестности их произведения существует окрестность N(x) точки х и окрестность N (y), точки y такие, что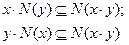

Выражение следует понимать как множество, образованное произведением элемента х на все элементы из N (y).

Таким образом, операция умножения двух элементов в топологическом пространстве непрерывно по каждому из сомножителей.

На рисунке 1 приведена схема, позволяющая более наглядно представить взаимосвязь вводимых понятий.

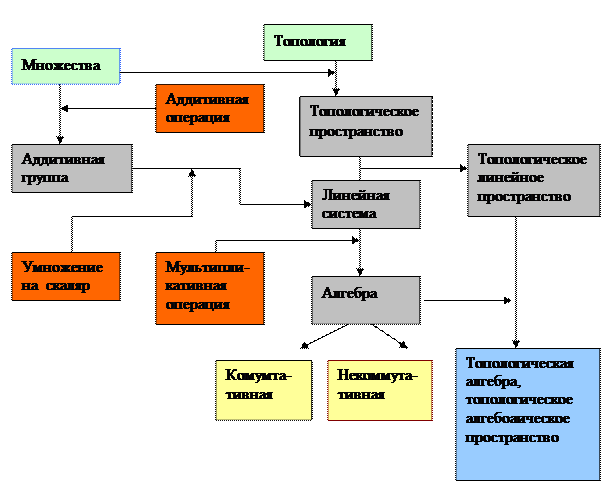
Рис.п.2.1 Связь вводимых понятий 1