Об уравнениях в частных производных
Из всех возможных типов уравнений в частных производных мы рассмотрим только линейные уравнения, т.е. уравнения, представляющие собой линейные комбинации искомой функции и ее производных, коэффициентами которых являются известные функции. Кроме того, мы ограничимся, в основном, уравнениями, содержащими производные не выше второго порядка.
Уравнения, которые мы будем рассматривать, как правило, связаны с математической формулировкой физических задач, с математическим описанием разных физических процессов.
Различают два типа процессов – нестационарные (меняющиеся во времени) и стационарные (не меняющиеся во времени). Нестационарные процессы описываются прежде всего уравнениями параболического и гиперболического типов, а стационарные процессы – уравнениями эллиптического типа.
Начнем со стационарных задач. Простейшим представителем уравнений эллиптического типа является уравнение Лапласа
 ,
,  ,
,
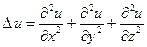 .
.
Мы будем его рассматривать только для случая двух независимых переменных
 ,
,  .
.
Неоднородное уравнение
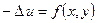
называется уравнение Пуассона.
Остановимся на формулировке краевых задач для эллиптических уравнений на примере уравнения Пуассона.
Пусть  конечная область на плоскости переменных
конечная область на плоскости переменных  . Границу
. Границу 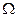 обозначим через
обозначим через 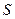 .
.
Для уравнения Пуассона ставятся следующие краевые задачи. Требуется найти в замкнутой области  решение
решение 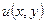 , удовлетворяющее в
, удовлетворяющее в 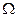 уравнению
уравнению
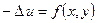 ,
, 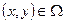 , (2.1)
, (2.1)
а на границе 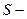 одному из следующих краевых условий:
одному из следующих краевых условий:
для первой краевой задачи
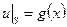 ,
, 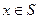 ; (2.2)
; (2.2)
для второй краевой задачи
 ,
, 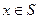 ; (2.3)
; (2.3)
для третьей краевой задачи
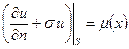 ,
, 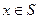 . (2.4)
. (2.4)
Здесь 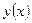 ,
, 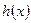 ,
, 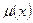 ,
,  заданные функции,
заданные функции,  производная по направлению внешней нормали к границе
производная по направлению внешней нормали к границе 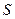 .
.
Первая краевая задача для уравнения Пуассона возникает, например, при отыскании положения равновесия 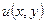 упругой однородной мембраны, закрепленной на границе
упругой однородной мембраны, закрепленной на границе 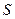 и находящейся под воздействием внешней силы
и находящейся под воздействием внешней силы 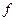 .
.
Другая физическая задача, для которой математическим описанием служит уравнение Пуассона – это задача о стационарном распределении температуры в однородной среде. В этом случае
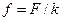 ,
,
где  плотность тепловых источников,
плотность тепловых источников,  коэффициент теплопроводности. В случае первой краевой задачи заданной оказывается температура на границе, во второй задаче задается тепловой поток, в случае третьей краевой задачи происходит теплообмен с внешней средой по закону Ньютона.
коэффициент теплопроводности. В случае первой краевой задачи заданной оказывается температура на границе, во второй задаче задается тепловой поток, в случае третьей краевой задачи происходит теплообмен с внешней средой по закону Ньютона.
Типичным представителем уравнений параболического типа является уравнение теплопроводности. В случае изотропной среды уравнение имеет вид
 ,
, 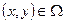 ,
, 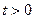 , (2.5)
, (2.5)
где
 ,
,
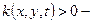 коэффициент теплопроводности. При
коэффициент теплопроводности. При 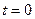 задается начальное условие
задается начальное условие
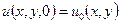 ,
, 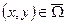 .
.
На границе области 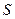 задается одно из краевых условий (2.2), (2.3) или (2.4).
задается одно из краевых условий (2.2), (2.3) или (2.4).
Простейшим примером уравнений гиперболического типа может служить уравнение колебаний струны
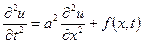 ,
, 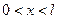 , (2.6)
, (2.6)
где 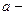 скорость распространения колебаний.
скорость распространения колебаний.
Начальные и граничные условия для этого уравнения:
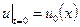 ,
, 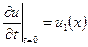 , (2.7)
, (2.7)
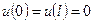 . (2.8)
. (2.8)
