Криволинейная трапеция. определенный интеграл, как предел интегральной суммы.геометрический смысл определенного интеграла

Криволинейной трапецией называется геометрическая фигура, ограниченная графиком непрерывной неотрицательной функции y = f (x), отрезками прямых x = a иx = b и отрезком [a; b] осиOX.

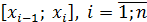Разобьем отрезок [a; b] на n‒ отрезков точками . На каждом отрезке выбираем точку 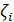(кси),

Построим прямоугольники с основанием: 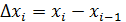и высотой

f( 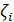), тогд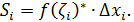а Сумма 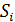называется интегральной суммой.

при 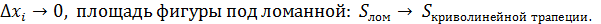Получим:

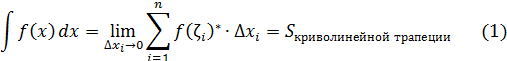
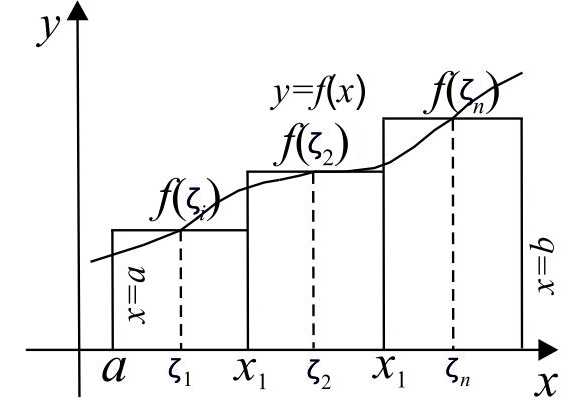
Рис. 16

Определенный интеграл, как предел интегральной суммы. Геометрический смысл определенного интеграла.

Определенным интегралом от функции f (x) на промежутке [a; b] называется предел интегральной суммы(1).

Геометрический смысл.

Определенный интеграл от непрерывной неотрицательной функции

f(x) на промежутке [a; b] численно равен площади соответствующей криволинейной трапеции:

Геометрические приложения определенного интеграла.

1. Вычисление S фигуры.

1) Если геометрическая фигура ограничена графиками двух непрерывных неотрицательных функций и .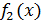

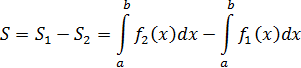
2) Если геометрическая фигура ограничена графиком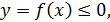

3) Если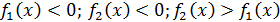

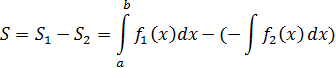
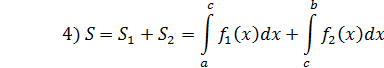
Пример.

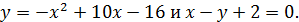
Решение:

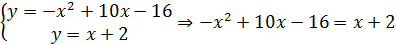
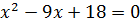
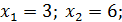
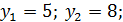
(3; 5), (6; 8) ‒ точки пересечения линии.

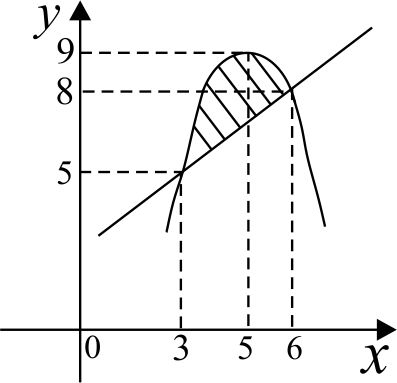
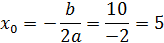
Второй способ:

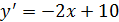
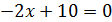
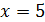
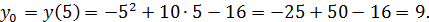
(5; 9) ‒ вершина параболы.

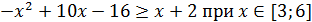
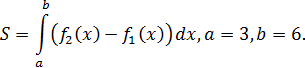
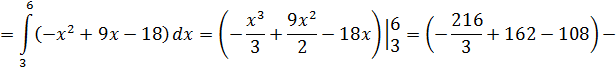
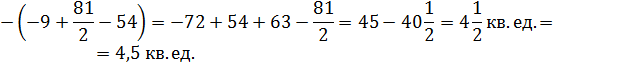
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ.

.

Задачи, приводящие к дифференциальным уравнениям.

1. Задача о нахождении закона движения материальной точки.

Обозначив 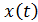‒ путь в момент времени 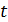, ‒скорость, тогда из физического смысла производной следует, что

или

Если 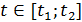, то получим , проинтегрировав это равенство, получим закон движения:

2. Задача о размножении бактерий.

Пусть 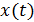‒ число бактерий в момент времени 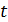.Так как скорость размножения бактерий пропорциональна их количеству, то по аналогии с предыдущим.

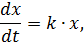
где 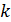‒ коэффициент пропорциональности.

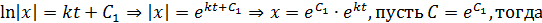
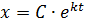
Основные понятия и определения теории дифференциальных уравнений.

1. Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию yи ее производные или дифференциалы.

Порядком дифференциального уравнения называется порядок старшей производной, входящей в него.

Пример.

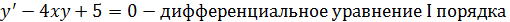
Решением дифференциального уравнения называется функция, обращающая его в тождество.

Общим решением дифференциального уравнения называется решение, содержащее столько произвольных постоянных C, каков порядок дифференциального уравнения.

так как

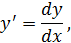
то

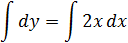
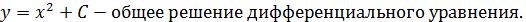
Частное решение дифференциального уравнения получается из общего решения при определенных начальных значениях независимой переменной и искомой функции.

Задача нахождения частного решения дифференциального уравнения называется задачей Каши.

Геометрически общее решение дифференциального уравнения представляет собой семейство интегральных кривых; частное решение ‒ единственная кривая, проходящая через данную точку 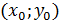.