Общая задача оптимизации
Общей задачей оптимизации называют задачу отыскания максимального или минимального значения для вещественного функционала J, заданного на множестве M. В частности, если М представляет собой отрезок вещественных чисел, то получится задача оптимизации функции.
Пусть 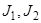 оба функционалы на множестве М;
оба функционалы на множестве М; 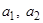 –вещественные числа. Символом
–вещественные числа. Символом 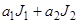 обозначается функционал на множестве М, который каждому x из М ставит в соответствие число
обозначается функционал на множестве М, который каждому x из М ставит в соответствие число
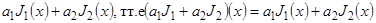 . Таким образом множество всех функционалов на множестве М образует векторное пространство над полем вещественных чисел.
. Таким образом множество всех функционалов на множестве М образует векторное пространство над полем вещественных чисел.
Рассмотрим задачу минимизации функционала J на множестве М. Под решением такой задачи понимают любой элемент m из множества М, удовлетворяющий условию:
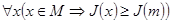 .
.
Такой m называют ещё оптимальным (или минимальным) элементом множества М относительно функционала J, а соответствующее число 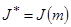 – значением задачи или оптимальным (минимальным) значением функционала J. В этом случае пишут
– значением задачи или оптимальным (минимальным) значением функционала J. В этом случае пишут
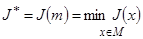 .
.
Аналогично рассматривается задача максимизации функционала. Заметим, что задача максимизации функционала J на множестве М эквивалентна задаче минимизации функционала 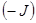 на этом же множестве (задачи имеют одинаковые решения).
на этом же множестве (задачи имеют одинаковые решения).
Пусть J есть функционал на множестве М. Число a называют нижней гранью функционала J, если 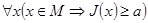 . Наибольшая нижняя грань функционала J называется точной нижней гранью функционала J и обозначается через
. Наибольшая нижняя грань функционала J называется точной нижней гранью функционала J и обозначается через 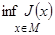 . Последнее эквивалентно существованию последовательности
. Последнее эквивалентно существованию последовательности 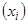 элементов множества М (минимизирующая последовательность) и такой, что
элементов множества М (минимизирующая последовательность) и такой, что
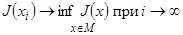 .
.
Двойственным образом определяются верхняя грань функционала J и точная нижняя грань функционала J; последняя обозначается через 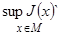 .
.
Можно поставить задачу нахождения точной нижней грани функционала J. Под решением такой задачи понимается любая соответствующая минимизирующая последовательность, а под значением–точная нижняя грань функционала J. Ясно, что задача нахождения точной нижней грани функционала обобщает задачу нахождения минимума этого же функционала.
Если функционал J на множестве М имеет хотя бы одну нижнюю грань, то он называется ограниченным снизу на множестве М. Ограниченность снизу функционала на множестве гарантирует существование решения задачи нахождения точной нижней грани функционала на этом множестве.
Т е о р е м а 1. Если функционал J на множестве М ограничен снизу, то найдётся последовательность 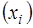 элементов множества М и такая, что
элементов множества М и такая, что 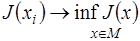 при
при 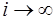 .
.
Д о к а з а т е л ь с т в о. Рассмотрим множество 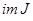 (образ функционала J) всевозможных значений функционала J. По условию это множество вещественных чисел, ограниченное снизу. Пусть m есть точная нижняя грань множества im J. Существование такого числа следует из теоремы о существовании точной нижней грани для ограниченного снизу числового множества. Число m удовлетворяет двум условиям: во-первых
(образ функционала J) всевозможных значений функционала J. По условию это множество вещественных чисел, ограниченное снизу. Пусть m есть точная нижняя грань множества im J. Существование такого числа следует из теоремы о существовании точной нижней грани для ограниченного снизу числового множества. Число m удовлетворяет двум условиям: во-первых 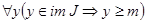 ; во-вторых, существует последовательность
; во-вторых, существует последовательность 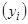 элементов множества im J, которая сходится к m. Поскольку каждый
элементов множества im J, которая сходится к m. Поскольку каждый 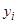 является значением функционала J на некотором
является значением функционала J на некотором 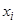 , то отсюда следует утверждение теоремы.
, то отсюда следует утверждение теоремы.
Если m не принадлежит множеству im J, то задача нахождения минимума функционала J не имеет решения, но если J ограничен снизу на М, то решение задачи нахождения точной нижней грани этого функционала (т.е. соответствующая минимизирующая последовательность) может рассматриваться как приближённое решение первой задачи.
Пример 1. Пусть 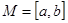 и J –неубывающая функция на этом отрезке. Тогда задача нахождения минимального значения J имеет решение: J(a). Если же
и J –неубывающая функция на этом отрезке. Тогда задача нахождения минимального значения J имеет решение: J(a). Если же 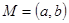 , то с тем же функционалом указанная задача не имеет решения. В этом случае в качестве приближённого решения можно взять произвольную минимизирующую последовательность; например,
, то с тем же функционалом указанная задача не имеет решения. В этом случае в качестве приближённого решения можно взять произвольную минимизирующую последовательность; например,
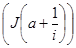 .
.
Пример 2. Множество М (соответственно V) представляет собой множество всех непрерывных функций 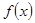 , заданных на отрезке
, заданных на отрезке 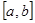 и удовлетворяющих на этом отрезке условию
и удовлетворяющих на этом отрезке условию 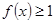 (соответственно
(соответственно 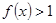 ). Зададим функционал соотношением
). Зададим функционал соотношением
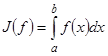 .
.
Точная нижняя грань функционала равна 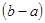 на обоих множествах. Она достигается на множестве М на функции
на обоих множествах. Она достигается на множестве М на функции 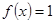 , так как
, так как
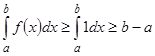 .
.
Минимизирующей последовательностью на множестве V будет, например, последовательность 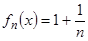 . При этом соответствующие значения функционала стремятся к точной
. При этом соответствующие значения функционала стремятся к точной
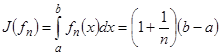
нижней грани функционала при 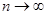 .
.
Пример 3. Частным примером общей задачи оптимизации является задача математического программирования. В этом случае множество М состоит из всех векторов 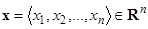 арифметического n-мерного пространства над полем вещественных чисел
арифметического n-мерного пространства над полем вещественных чисел 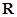 , удовлетворяющих следующей системе уравнений и неравенств:
, удовлетворяющих следующей системе уравнений и неравенств:
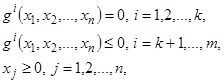 (1)
(1)
где 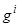 –непрерывные функции. Функционал в этой задаче является непрерывной функцией
–непрерывные функции. Функционал в этой задаче является непрерывной функцией 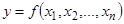 , называемой ещё целевой функцией. Любой вектор, удовлетворяющий системе (1), называется допустимым. Задача заключается в том, чтобы найти допустимый вектор, на котором целевая функция принимает минимальноё значение. Если найдётся число с и такое, что множество допустимых векторов x, удовлетворяющих условию
, называемой ещё целевой функцией. Любой вектор, удовлетворяющий системе (1), называется допустимым. Задача заключается в том, чтобы найти допустимый вектор, на котором целевая функция принимает минимальноё значение. Если найдётся число с и такое, что множество допустимых векторов x, удовлетворяющих условию 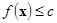 , ограничено, то оно компактно (замкнутость этого множества очевидна). По теореме Вейерштрасса непрерывная функция достигает максимального и минимального своих значений на компактном множестве. Следовательно указанные условия достаточны для существования (точного) решения задачи математического программирования. Если же эти условия не выполнены, то в качестве приближённого решения задачи можно использовать любую минимизирующую последовательность.
, ограничено, то оно компактно (замкнутость этого множества очевидна). По теореме Вейерштрасса непрерывная функция достигает максимального и минимального своих значений на компактном множестве. Следовательно указанные условия достаточны для существования (точного) решения задачи математического программирования. Если же эти условия не выполнены, то в качестве приближённого решения задачи можно использовать любую минимизирующую последовательность.
