Основные теоремы дифференциального исчисления
Теорема. (Ролль) Если функция  непрерывна на отрезке
непрерывна на отрезке 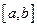 , дифференцируема на интервале
, дифференцируема на интервале 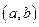 и значения функции на концах отрезка равны
и значения функции на концах отрезка равны  , то на интервале
, то на интервале 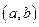 существует точка
существует точка 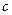 ,
, 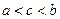 , в которой производная функция
, в которой производная функция  равная нулю:
равная нулю: 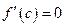 .
.
Геометрический смысл теоремы Ролля состоит в том, что при выполнении условий теоремы на интервале 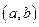 существует точка
существует точка 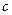 такая, что в соответствующей ей точке кривой
такая, что в соответствующей ей точке кривой 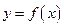 касательная параллельна оси
касательная параллельна оси 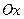 . Таких точек на интервале
. Таких точек на интервале 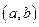 может быть несколько, но теорема утверждает существование по крайней мере одной такой точки.
может быть несколько, но теорема утверждает существование по крайней мере одной такой точки.
Доказательство. По свойству функций, непрерывных на отрезке функция  на отрезке
на отрезке 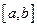 принимает наибольшее и наименьшее значения. Обозначим эти значения
принимает наибольшее и наименьшее значения. Обозначим эти значения 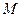 и
и 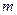 соответственно. Возможны два различных случая
соответственно. Возможны два различных случая  и
и  .
.
Пусть  . Тогда функция
. Тогда функция  на отрезке
на отрезке 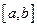 сохраняет постоянное значение и в любой точке интервала ее производная равна нулю. В этом случае за
сохраняет постоянное значение и в любой точке интервала ее производная равна нулю. В этом случае за 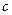 можно принять любую точку интервала.
можно принять любую точку интервала.
Пусть  . Так как значения на концах отрезка равны, то хотя бы одно из значений
. Так как значения на концах отрезка равны, то хотя бы одно из значений 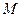 или
или 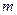 функция принимает внутри отрезка
функция принимает внутри отрезка 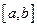 . Обозначим через
. Обозначим через 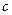
 точку, в которой
точку, в которой 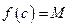 . Так как
. Так как 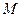 - наибольшее значение функции, то для любого
- наибольшее значение функции, то для любого 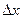 (будем считать, что точка
(будем считать, что точка 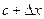 находится внутри рассматриваемого интервала) верно неравенство:
находится внутри рассматриваемого интервала) верно неравенство:
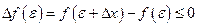 .
.
При этом  Но так как по условию производная в точке
Но так как по условию производная в точке 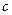 существует, то существует и предел
существует, то существует и предел 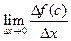 .
.
Т.к.  и
и  , то можно сделать вывод:
, то можно сделать вывод:
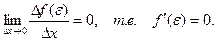
Теорема доказана.
Теорема Ролля имеет несколько следствий:
1) Если функция  на отрезке
на отрезке 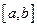 удовлетворяет теореме Ролля, причем
удовлетворяет теореме Ролля, причем 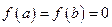 , то существует по крайней мере одна точка
, то существует по крайней мере одна точка 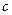
 , такая, что
, такая, что 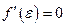 . Т.е. между двумя нулями функции найдется хотя бы одна точка, в которой производная функции равна нулю.
. Т.е. между двумя нулями функции найдется хотя бы одна точка, в которой производная функции равна нулю.
2) Если на рассматриваемом интервале 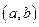 функция
функция  имеет производную
имеет производную 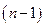 - го порядка и
- го порядка и 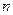 раз обращается в нуль, то существует по крайней мере одна точка интервала, в котором производная
раз обращается в нуль, то существует по крайней мере одна точка интервала, в котором производная 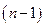 – го порядка равна нулю.
– го порядка равна нулю.
Теорема.(Лагранж)Если функция  непрерывна на отрезке
непрерывна на отрезке 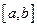 и дифференцируема на интервале
и дифференцируема на интервале 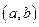 , то на этом интервале найдется по крайней мере одна точка
, то на этом интервале найдется по крайней мере одна точка 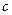
 такая, что
такая, что 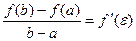 .
.
Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.
Отношение 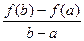 равно угловому коэффициенту секущей
равно угловому коэффициенту секущей 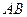 .
.
 у
у
В
А
0 а e b x
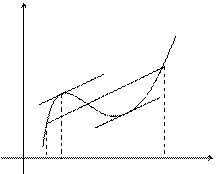
Если функция  удовлетворяет условиям теоремы, то на интервале
удовлетворяет условиям теоремы, то на интервале 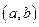 существует точка
существует точка 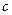 такая, что в соответствующей точке кривой
такая, что в соответствующей точке кривой 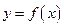 касательная параллельна секущей, соединяющей точки
касательная параллельна секущей, соединяющей точки 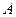 и
и 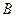 . Таких точек может быть и несколько, но одна существует обязательно.
. Таких точек может быть и несколько, но одна существует обязательно.
Доказательство. Рассмотрим некоторую вспомогательную функцию
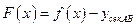
Уравнение секущей АВ можно записать в виде:

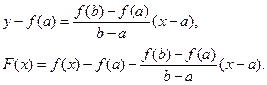
Функция 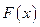 удовлетворяет теореме Ролля. Действительно, она непрерывна на отрезке
удовлетворяет теореме Ролля. Действительно, она непрерывна на отрезке 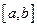 и дифференцируема на интервале
и дифференцируема на интервале 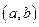 . По теореме Ролля существует хотя бы одна точка
. По теореме Ролля существует хотя бы одна точка 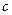
 , такая что
, такая что 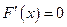 .
.
Так как 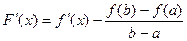 , то
, то 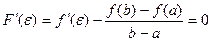 , следовательно
, следовательно
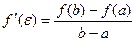 .
.
Теорема доказана.
Определение. Выражение 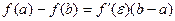 называется формулой
называется формулой
Лагранжаили формулой конечных приращений.
В дальнейшем эта формула будет очень часто применяться для доказательства самых разных теорем. Иногда формулу Лагранжа записывают в несколько другом виде:
 ,
,
где 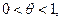
 ,
, 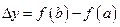 .
.
Теорема. (Коши) Если функции  и
и 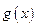 непрерывны на отрезке
непрерывны на отрезке 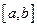 и дифференцируемы на интервале
и дифференцируемы на интервале 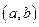 и
и  на интервале
на интервале 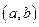 , то существует по крайней мере одна точка
, то существует по крайней мере одна точка 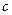 ,
, 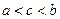 , такая, что
, такая, что
 .
.
Т.е. отношение приращений функций на данном отрезке равно отношению производных в точке 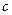 .
.
Доказательство. Рассмотрим вспомогательную функцию
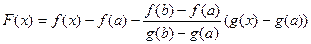 ,
,
удовлетворяющая на отрезке 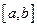 условиям теоремы Ролля. Очевидно, что при
условиям теоремы Ролля. Очевидно, что при 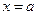 и
и 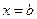
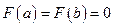 . Тогда по теореме Ролля существует такая точка
. Тогда по теореме Ролля существует такая точка 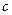
 , такая, что
, такая, что 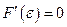 . Так как
. Так как
 , то
, то 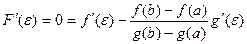
С другой стороны 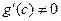 . Следовательно,
. Следовательно, 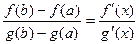 .
.
Теорема доказана.
Следует отметить, что рассмотренная выше теорема Лагранжа является частным случаем (при 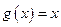 ) теоремы Коши. Доказанная нами теорема Коши очень широко используется для раскрытия так называемых неопределенностей. Применение полученных результатов позволяет существенно упростить процесс вычисления пределов функций, что будет подробно рассмотрено ниже.
) теоремы Коши. Доказанная нами теорема Коши очень широко используется для раскрытия так называемых неопределенностей. Применение полученных результатов позволяет существенно упростить процесс вычисления пределов функций, что будет подробно рассмотрено ниже.
