Задача с разрывными коэффициентами
Пусть 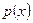 терпит разрыв в точке
терпит разрыв в точке 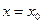 ,
, 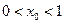 . Что понимать под решением (1.4) – не очень понятно, так как дифференцирование в точке
. Что понимать под решением (1.4) – не очень понятно, так как дифференцирование в точке 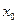 неосуществимо. В этом случае принято ставить задачу так: решением задачи (1.4), (1.5) называют функцию, удовлетворяющую (1.4) при
неосуществимо. В этом случае принято ставить задачу так: решением задачи (1.4), (1.5) называют функцию, удовлетворяющую (1.4) при 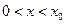 ,
, 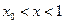 и определенным условиям в точке разрыва. Исходя из физических соображений в точке разрыва, например, ставят условия непрерывности решения и непрерывности функции
и определенным условиям в точке разрыва. Исходя из физических соображений в точке разрыва, например, ставят условия непрерывности решения и непрерывности функции 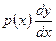 , т.е. требуют выполнения равенств (условий сопряжения)
, т.е. требуют выполнения равенств (условий сопряжения)
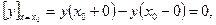 (1.8)
(1.8)
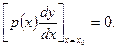 (1.9)
(1.9)
Если задача (1.4), (1.5), например, описывает распределение температуры в стержне, то условие (1.9) означает непрерывность потока тепла.
Решение задачи (1.4), (1.5), (1.8), (1.9) удовлетворяет уравнению (1.7). Действительно, умножим (1.4) на 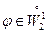 и проинтегрируем по (0, 1). После интегрирования по частям получим
и проинтегрируем по (0, 1). После интегрирования по частям получим
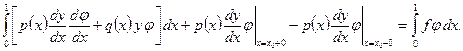 (1.10)
(1.10)
В силу (1.9) это равенство совпадает с (1.7). Таким образом, краевая задача (1.4), (1.5) в случае разрыва 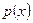 имеет обобщенное решение, принадлежащее
имеет обобщенное решение, принадлежащее 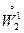 , но не принадлежащее
, но не принадлежащее 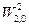 . В этом легко убедиться на примере. Рассмотрим задачу
. В этом легко убедиться на примере. Рассмотрим задачу
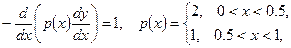
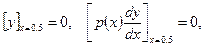
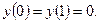
Решением этой задачи является функция
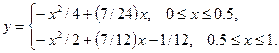
Эта функция принадлежит пространству 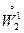 , но не принадлежит пространству
, но не принадлежит пространству 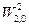 , так как ее первая производная терпит разрыв.
, так как ее первая производная терпит разрыв.
Если обобщенное решение задачи (1.4), (1.5), (1.8), (1.9) имеет вторые производные на промежутках 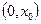 ,
, 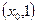 , то условие (1.9) выполняется автоматически: оно является свойством решения уравнения (1.7). Это нетрудно показать. Проводя в (1.7) интегрирование по частям, получаем
, то условие (1.9) выполняется автоматически: оно является свойством решения уравнения (1.7). Это нетрудно показать. Проводя в (1.7) интегрирование по частям, получаем
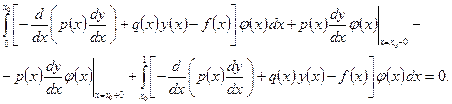
Отсюда ввиду произвольности 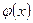 следует, что условие (1.9) выполнено. Автоматизм выполнения условий (1.9) позволяет называть это условие естественным.
следует, что условие (1.9) выполнено. Автоматизм выполнения условий (1.9) позволяет называть это условие естественным.
Иногда вместо условий сопряжения (1.8), (1.9) используют другие. Например, вместо (1.9) рассматривают условие
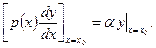 (1.11)
(1.11)
Использование в этом случае обобщенной постановки задачи (1.4), (1.5), (1.8), (1.11) особенно целесообразно. В силу (1.10) и (1.11)
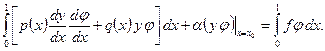 (1.12)
(1.12)
Это уравнение играет туже роль, что и уравнение (1.7). С помощью (1.12) очевидным образом определяется обобщенное решение задачи (1.4), (1.5), (1.8), (1.11). Условие (1.11), так же как и (1.9), является естественным. Использование обобщенной постановки в виде уравнения (1.12) удобнее для построения численного метода, так как непосредственная аппроксимация условия (1.11) не проста.
Итак, обобщенная формулировка задач обладает целым рядом преимуществ по сравнению с дифференциальным уравнением.
Краевая задача (1.4), (1.5) называется первой краевой задачей, а условия (1.5) – краевыми условиями первого рода.
Рассмотрим теперь краевую задачу для уравнения (1.4) с условиями
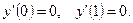 (1.13)
(1.13)
Задачу (1.4), (1.13) называют второй краевой задачей, а условие (1.13) – краевым условием второго рода.
При тех же требованиях на коэффициенты, что и для первой краевой задачи, решение задачи (1.4), (1.13) принадлежит 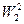 . Наряду с
. Наряду с 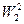 рассмотрим пространство
рассмотрим пространство 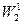 . Значок ''нолик'' здесь отсутствует. Это означает, что на концах отрезка функции не подчинены никаким граничным условиям, т.е. они ''свободны''.
. Значок ''нолик'' здесь отсутствует. Это означает, что на концах отрезка функции не подчинены никаким граничным условиям, т.е. они ''свободны''.
Обобщенное решение (1.4), (1.13) определяется как функция из 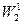 , удовлетворяющая (1.7) при произвольных
, удовлетворяющая (1.7) при произвольных 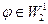 .
.
Различие в определении обобщенных решений для второй и первой краевых задач состоит в том, что обобщенное решение второй краевой задачи ищется среди функций, ''свободных'' на концах отрезка (0, 1).
Если обобщенное решение принадлежит 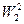 , то нетрудно показать, что оно удовлетворяет краевым условиям (1.13). Интегрируя по частям, получим
, то нетрудно показать, что оно удовлетворяет краевым условиям (1.13). Интегрируя по частям, получим
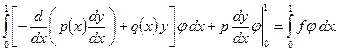
Откуда, ввиду произвольности 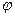 , получим, что
, получим, что 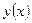 удовлетворяет как уравнению (1.4), так и краевым условиям (1.13). Условия (1.13), так же как и (1.9), выполняются для решения автоматически. Про них говорят, что они естественные.
удовлетворяет как уравнению (1.4), так и краевым условиям (1.13). Условия (1.13), так же как и (1.9), выполняются для решения автоматически. Про них говорят, что они естественные.
Это свойство краевых условий будет использоваться при построении приближенных решений. Оно позволяет искать приближенное решение среди функций, свободных на границе. Следовательно, от координатных функций можно не требовать, чтобы они удовлетворяли краевым условиям.
