Испытания и соб-я. Виды событий. Операции над событиями

Эл-ты комбинаторики. Размещения. Перестановки. Сочетания.

Комбинаторика – это раздел эл-ной мат-ки, в кот. рассм-ся вопрос о кол-ве комбинаций, кот. можно сост-ть при опред. усл-ях в зад. объектах.

Картежем наз. упорядоченная n (энка) элементов а₁, а₂,…а_n.

Декартовое произведение A₁,A₂ множест наз-ся мн-во всех картежей длины К (а₁,а₂…а_к), где а₁ ?А₁, а₂? А_{2 …}а_к?А_к и обознач-ся А₁*А₂*…*А_к.

Мн-во сост. из n-элементов-n-мн-во.

При решении задач комбинаторики используют след. правила:

Правило суммы. Если некоторый объект А м. б. выбран из совокупности объектов m способами, а др. объект В может быть выбран n сп-ми, то выбрать либо А, либо В можно m+n сп-ми.

Пусть в корзине имеется 7 апельсинов, 5 бананов и 10 яблок. Тогда выбор одного из фруктов (или апельсина, или банана, или яблока) можно сделать 22 способами (22 = 7 + 5 +10).

Правило произведения. Если объект А можно выбрать из сов-ти объектов m сп-ми и после каждого такого выбора объект В можно выбрать n сп-ми, то пара объектов (А, В) в указ. порядке м. б. выбрана mn способами.

Пример. В универ. столовой в меню 1-ых блюд-2, 2-7, 3-4.Каим СП-бом можно пообедать? 2*7*4=56

Перестановками называются комбинации, состоящие из одних и тех же элементов, отличающихся друг от друга только их порядком, обозначается 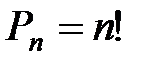Пример: Сколько трехзначных чисел можно составить из 3-х различных цифр?

123, 132, 213,231,312,321

Р₃=3!

Размещениемназывается комбинации из п- различных элементов по т – элементов, которые отличаются либо составом элементов, либо их порядком, обозначается:

Пример. В гр. 25 студ-ов. Какими СП-ми можно выбрать старосту и зам. старосты? n=25,k=2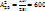

Сочетаниями называются комбинации, составленные из п различных элементов по т элементов, которые отличаются хотя бы одним элементом, обозначается: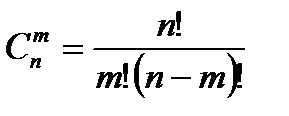

Пример. В студ. гр. 25 чел. Какими СП-ми можно выбрать дежурных?

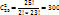
Испытания и соб-я. Виды событий. Операции над событиями.

Испытанием наз. эксперимент, кот. в один. усл-ях можно проводить любое число раз(бросание монеты, кости).

Простейший рез-т испытания наз. исходом испытания, или эл-ным событием (w). Мн-во всех исходов испыт-я наз. осн. пространством, или пр-вом эл-ных событий, или достоверным событием.

При испытании неизбежно наступает какой-то исход и при том только 1.

Событием называется исход испытания. Это понятие явля­ется первичным в теории вероятностей. События обозначаются большими латинскими буквами А, В, С,... .

Исходы, из кот. сост. событие А, наз. благопр-ми для события А

События:

1). Случайные(любое мн-во исходов);

2). Достоверные;

3). Невозможные(пустое мн-во исходов).

Достоверным называется событие, которое обязательно происходит при осуществлении определен­ного комплекса условий. Обозначение: Ω.

Невозможным называется событие, которое по аналогии заведомо не происходит при осуществлении определенного комплекса условий. Обозначение: Ø.

Случайным называется событие, которое может произойти или не произойти.

Виды СС:

1)События называются несовместными, если в одном испытании появление одного события исклю­чает появление другого(соб. А и В не имеют общих исходов).

2)Несколько событий образуют полную группу, если в результате испытания появится одно из них. Т.е. событие появления хотя бы одного из событий полной группы будет достоверным. Если события полной группы попарно несовместны, то в результате испытания произойдет только одно из событий полной группы.

Совместные-имеющие общ. исходы.

События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Операции

Событие А влечет за собой событие В, если из наступле­ния события А следует наступление события В. Этот факт обо­значается А с В. В терминах элементарных событий это означа­ет, что каждое элементарное событие, входящее в А, входит так­же и в В.

Равенство событий А = В означает, что А с В и В с А, т.е. они состоят из одних и тех же элементарных событий.

Суммой событий Aw В называется такое событие С = А+ В, которое означает наступление или А, или В, т.е. хотя бы одного из них.

Произведением событий А и В называется событие, состоя­щее в совместном наступлении события А и события В, и обо­значается С = А * В.

Несовместными называются события А и В, если их произ­ведение является невозможным событием, т.е. А* В =0.

Дополнением к событию А называется событие А, которое можно определить равенствами: А- А = и А + A =Ω.

Разностью событий A и В называется событие, состоящее в наступлении А и ненаступлении В. Разность А и В обозначается А - В и характеризуется условием А- В=А* В.

Операции над событиями можно представить как операции над множествами. При этом события представляются подмноже­ствами некоторого множества Ω. Сумме событий А + В соответст­вует объединение A В этих подмножеств, а их произведению А*В — пересечение А В. Достоверное событие представляется объемлющим множеством Ω, а невозможное событие — пустым подмножеством в нем. Несовместность событий А и В означа­ет, что соответствующие подмножества А и В не пересекаются: А В= . Событие А, противоположное событию А, является дополнением к событию А во множестве Ω. Эти операции в гра­фическом виде иллюстрируются диаграммами Венна.