Дискретные случайные величины. Числовые характеристики случайных величин
Случайная величина, которая может принимать только конечное или счетное мн-во значений называется дискретной. Значение случайной дискретной величины можно записать в виде конечной или бесконечной последовательности х1, х2, х3… . Законом распределения дискретной случайной величины называется соответствие между значениями х1, х2, х3… этой величины и их вероятностями р1, р2, р3… Т.к. в результате испытания величина Х всегда примет одно из значений х1, х2,…, хn , то р1+р2+…+рn+…=  . З-н распределения дискретной случайной величины для наглядности изображают графиком, который называется многоугольником распределения случайной величины Х. Для этого в прямоугольно-декартовой системе координат строят точки с координатами (хк, рк) и соединяют их последовательно отрезками прямых. Т.о. имеются 2 способа задания дискретной случайной величины. Один с помощью ф-ии распределения, 2-ой с помощью закона распределения. Ф-ии распределения F(x) для дискретной случайной величины Х, которая может принимать значения х1, х2,…,хn с вероятностями имеет вид:
. З-н распределения дискретной случайной величины для наглядности изображают графиком, который называется многоугольником распределения случайной величины Х. Для этого в прямоугольно-декартовой системе координат строят точки с координатами (хк, рк) и соединяют их последовательно отрезками прямых. Т.о. имеются 2 способа задания дискретной случайной величины. Один с помощью ф-ии распределения, 2-ой с помощью закона распределения. Ф-ии распределения F(x) для дискретной случайной величины Х, которая может принимать значения х1, х2,…,хn с вероятностями имеет вид: 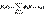 , где
, где  означает, что суммируются Р тех значений, которые меньше х.
означает, что суммируются Р тех значений, которые меньше х. 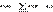 является разрывной. Математическим ожиданием дискретной случайной величины Х, принимающей конечное мн-во значений, с законом распределения
является разрывной. Математическим ожиданием дискретной случайной величины Х, принимающей конечное мн-во значений, с законом распределения 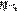 )=рк, к=
)=рк, к=  ,
, 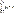 называется сумма произведений ее значений на их соответствующие вероятности. Т.е. М(Х)=х1р1+х2р2+…+хnpn=
называется сумма произведений ее значений на их соответствующие вероятности. Т.е. М(Х)=х1р1+х2р2+…+хnpn= 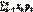 Математическое ожидание дискретной величины приближенно равно сумме всех ее возможных значений. Поэтому математическое ожидание случайной величины называется ее средним значением. Математическое ожидание дискретной случайной величины, принимающей бесконечную последовательность значений с законом распределения
Математическое ожидание дискретной величины приближенно равно сумме всех ее возможных значений. Поэтому математическое ожидание случайной величины называется ее средним значением. Математическое ожидание дискретной случайной величины, принимающей бесконечную последовательность значений с законом распределения  )=рк, к=1,2,3…,
)=рк, к=1,2,3…,  опр-ся формулой:
опр-ся формулой: 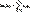 , если этот ряд сходится абсолютно; в противном случае считают, что у данной случайной величины нет математического ожидания. Св-ва математического ожидания случайной величины: Значение математического ожидания случайной величины Х заключено между ее наименьшим а и наибольшим значением в,т.е. а≤М(Х)≤в; Математическое ожидание постоянной величины равно этой постоянной М(С)=С, С – const; Постоянный множитель можно вынести за знак математического ожидания: М(СХ)=СМ(Х), С – cons.
, если этот ряд сходится абсолютно; в противном случае считают, что у данной случайной величины нет математического ожидания. Св-ва математического ожидания случайной величины: Значение математического ожидания случайной величины Х заключено между ее наименьшим а и наибольшим значением в,т.е. а≤М(Х)≤в; Математическое ожидание постоянной величины равно этой постоянной М(С)=С, С – const; Постоянный множитель можно вынести за знак математического ожидания: М(СХ)=СМ(Х), С – cons.
Математическое ожидание алгебраической суммы конечного числа случайной величины равно алгебраической сумме их математических ожиданий. Например,для двух случайных величн М(Х±У)=М(Х)±М(У). Отклонением случайной величины Х от ее математического ожидания (или отклонением случайной величины Х) наз. случайная величина Х-М(Х). Теорема: мат. ожидание отклонения Х-М(Х)=0, т.е. М(Х-М(Х))=0. Дисперсией случайной величины Х называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания, т.е. D(X)=М(Х-М(Х))2). Из определения и св-в математического ожидания следует, что дисперсия любой случайной величины неотрицательна, т.е. D(X)≥0. Легко показать, что дисперсия случайной величины Х равна разности между математическим ожиданием квадрата величины Х и квадратом ее математического ожидания, т.е. D(X)=М(Х)2-(М(Х))2. Св-ва дисперсии случайной величины: Дисперсия постоянной величины равна 0. D(С)=0;
постоянный множитель можно вынести за знак дисперсии, возводя его в квадрат, т.е. D(СX)=С2 D(X); дисперсия алгебраической суммы двух независимых случайных величин равна сумме их дисперсий, т.е. D(X±У)= D(X)+ D(У)
Дисперсия дискретной случайной величины с законом распределения 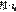 )=рк, к=
)=рк, к= 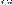 ,
,  опр-ся формулой
опр-ся формулой 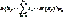 Если дискретная случайная величина принимает бесконечную последовательность значений с законом распределения
Если дискретная случайная величина принимает бесконечную последовательность значений с законом распределения 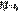 )=рк, к=1,2,3…,
)=рк, к=1,2,3…,  , то ее дисперсия опр-ся формулой:
, то ее дисперсия опр-ся формулой:
 , при условии, что этот ряд сходится (т.е.принимает какое-то значение). Средним квадратным отклонением (стандартным отклонением) случайной величины Х называется корень квадратный из ее дисперсии, т.е. δ(Х)=
, при условии, что этот ряд сходится (т.е.принимает какое-то значение). Средним квадратным отклонением (стандартным отклонением) случайной величины Х называется корень квадратный из ее дисперсии, т.е. δ(Х)=  .
.
