Б. Пример обработки результатов прямых многократных измерений
Найти диаметр шарика и соответствующую погрешность.
1. Пусть измерения диаметра шарика микрометром дали следующие результаты:
, 
, 
, 
, 
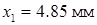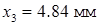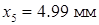, причем инструментальная погрешность микрометра 
.
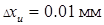2. Среднеарифметическое из всех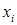 
т.е.
.
3. Тогда 
дает 
, 
, 
, 
, 
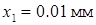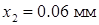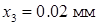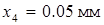и
.
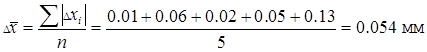4.Заметим, что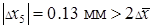 
. Поэтому 
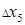является грубой погрешностью. Следовательно, замер 
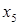ошибочен, и мы исключаем из дальнейших расчетов 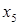и , и 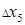. Поэтому 
.
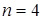5.Снова определяем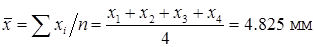 
, а также 
, 
, 
, 
.
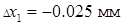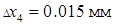6. Находим их квадраты 
;
; 
.
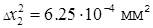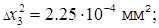
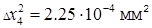7. Рассчитываем
.
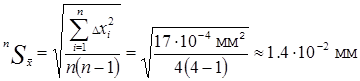8. Задаемся значением доверительной вероятност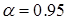и 
и
9. для 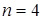находим 
(см. таблицу на с.20).
10. Получаем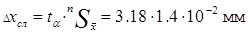 
.
11. В нашем случае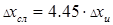 
. Поэтому полная погрешность
.
3.12. Окончательный результат:
; 
; 
; .
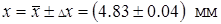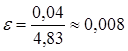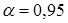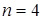Цифры в третьем десятичном разряде после запятой округляется, так как инструментальная погрешность равна 0,01 мм, т.е. соответствует единице 2 десятичного разряда.
8. Обработка результатов косвенных измерений
Пусть косвенно определяемая величина рассчитана по формуле, выражаемой функцией
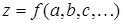, (16)
причем результаты прямых многократных измерений величин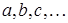 
уже известны, грубые погрешности исключены и рассчитаны величины 
, 
, 
, 
, 
, 
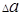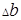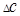,..., где 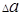, , 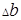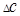– полные абсолютные погрешности прямых многократных измерений величин 
, 
, 
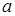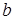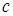,..., рассчитанных в соответствии с п.п. З–10 (см. стр.14) включительно. В качестве наилучшего приближения к истинному значению 
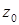принимают
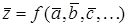. (17)
Случайные погрешности косвенно определяемой величины рассчитывают методом частных дифференциалов или методом дифференциала логарифма.
А. Метод частных дифференциалов
Частными производными функции нескольких переменных (в нашем случае 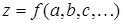) по одной из них называют выражения;
а) 
при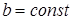 
, 
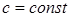и т.д.;
б)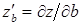 
при 
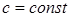, и т.д.;
в)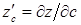 
при , 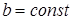и т.д.
Частную производную находят по правилам дифференцирования функций одной переменной, причем остальные переменные, кроме той, по которой берут частную производную, рассматриваются как постоянные. В случае а) роль переменной играет "а", а роль постоянных - "в","с" и т.д.
Частный дифференциал определяют равенством:
и т.д.
Итак, частные дифференциалы функции 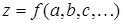имеют вид:
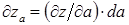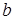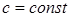
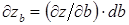при ,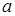
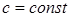
при ,
при ,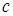 
В соответствии с этим за абсолютные погрешности принимают приращения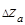 
, 
, 
,...
, 
, 
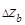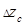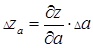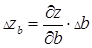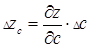, (18)
где 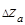- абсолютная погрешность косвенно определяемой величина, обусловленная погрешностью 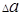только величины "а", 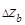- абсолютная погрешность косвенно определяемой величины, обусловленная погрешностью 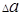только величины "в" и т.д.
Таким образом, полная абсолютная погрешность результата косвенных измерений должна быть рассчитана по формуле:
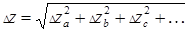. (19)