Основные свойства функций
Функции. Предел функции
Понятие функции. Способы задания функции
Определение. Пусть 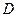 - произвольное множество действительных чисел:
- произвольное множество действительных чисел: 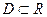 . Говорят, что задана функция
. Говорят, что задана функция 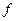 с областью определения D, если каждому числу
с областью определения D, если каждому числу  из множества D поставлено в соответствие единственное действительное число
из множества D поставлено в соответствие единственное действительное число 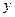 . Обозначение:
. Обозначение:
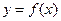 .
.
Читается: « 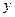 есть
есть 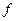 от
от  . Число
. Число  называется аргументом, число
называется аргументом, число 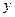 - значением функции
- значением функции 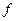 при данном значении
при данном значении  аргумента. Множество
аргумента. Множество  всех значений функции
всех значений функции 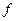 называется областью значений этой функции.
называется областью значений этой функции.
Определение. Графиком функции 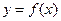 называется множество точек
называется множество точек 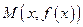 координатной плоскости, где
координатной плоскости, где  «пробегает» всю область определения
«пробегает» всю область определения 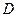 .
.
Основными способами задания функции являются: аналитический (т.е. с помощью формулы, выражающей 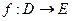 ), графический, табличный и словесный.
), графический, табличный и словесный.
При аналитическом задании функции обычно считается, что область ее определения совпадает с областью допустимых значений (ОДЗ) аргумента  в формуле
в формуле 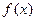 . Например, областью определения функции
. Например, областью определения функции

является множество 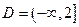 .
.
Примером словесного задания функции является функция Дирихле: 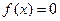 , если
, если  - иррациональное число,
- иррациональное число, 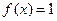 если
если  - рациональное число.
- рациональное число.
Заметим, что числовая последовательность - это функция с областью определения 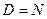 . В этом случае вместо
. В этом случае вместо  пишут просто
пишут просто 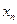 .
.
Основные свойства функций
Функция 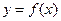 с областью определения
с областью определения 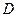 называется четной (нечетной), если для любого
называется четной (нечетной), если для любого 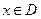 ,
,  выполняется равенство:
выполняется равенство:
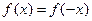
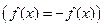 .
.
Функция 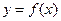 с областью определения
с областью определения 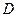 называется периодической, если существует действительное число
называется периодической, если существует действительное число  такое, что, если
такое, что, если 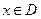 и
и 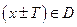 , то
, то

для любого 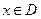 .
.
Наименьшее из таких чисел называется периодом функции 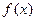 .
.
Например, функции 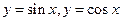 являются периодическими с периодом
являются периодическими с периодом 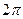 , а функции
, а функции  - также периодические, но с периодом
- также периодические, но с периодом 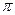 .
.
Функция 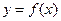 называется возрастающей (убывающей) на множестве
называется возрастающей (убывающей) на множестве 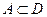 , если для любых
, если для любых 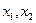 из А таких, что
из А таких, что 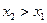 , выполняется неравенство
, выполняется неравенство
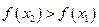
 .
.
Функция возрастающая (убывающая) на множестве А называется монотонной на этом множестве.
Пусть 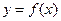 - монотонная функция на множестве
- монотонная функция на множестве 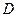 и
и 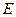 - множество ее значений.
- множество ее значений.
Функция  с областью определения
с областью определения 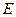 называется обратной по отношению к функции
называется обратной по отношению к функции 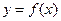 , если для любого
, если для любого  из
из 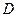
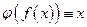 .
.
Из этого определения следует, что график обратной функции  получается симметрированием графика данной функции
получается симметрированием графика данной функции 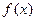 относительно биссектрисы 1го и 3го координатных углов.
относительно биссектрисы 1го и 3го координатных углов.
Например, функций 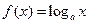 и
и 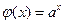 – взаимно-обратные.
– взаимно-обратные.
Пусть 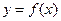 - функция с областью определения
- функция с областью определения 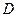 , а
, а 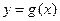 - функция с областью определения
- функция с областью определения  . Обозначим через
. Обозначим через 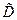 множество тех значений аргумента
множество тех значений аргумента  , для которых
, для которых 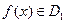 . Тогда говорят, что на множестве
. Тогда говорят, что на множестве 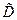 определена сложная функция
определена сложная функция
 .
.
Окрестностью точки 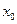 называется всякий открытый интервал с центром в точке
называется всякий открытый интервал с центром в точке 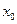 ;
;  - окрестностью точки
- окрестностью точки 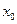 называется интервал
называется интервал 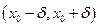 .
.
Пусть 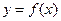 - функция с областью определения
- функция с областью определения 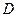 . Точка
. Точка  называется точкой максимума (минимума), если существует
называется точкой максимума (минимума), если существует  -окрестность точки
-окрестность точки 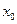 такая, что для всех
такая, что для всех  из этой
из этой  -окрестности выполняются неравенства:
-окрестности выполняются неравенства:

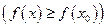
(от лат. maximum - наибольшее, minimum - наименьшее).
Точки максимума и минимума функции 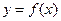 называются точками экстремума (от лат. extremum - крайнее), а значения функции
называются точками экстремума (от лат. extremum - крайнее), а значения функции 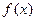 в этих точках - экстремумами функции.
в этих точках - экстремумами функции.
В точках экстремума функция 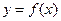 меняет область своего возрастания (убывания) на область убывания (возрастания), т.е. в окрестности точки максимума график функции - «холм», а в окрестности точки минимума - «впадина».
меняет область своего возрастания (убывания) на область убывания (возрастания), т.е. в окрестности точки максимума график функции - «холм», а в окрестности точки минимума - «впадина».
Наибольшим (наименьшим) значением функции 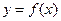 в области
в области 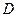 называется такое число
называется такое число 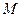 (число
(число 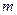 ), что для всех
), что для всех  из
из 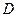

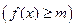 . Если функция
. Если функция 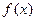 задана на отрезке
задана на отрезке 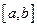 и ее график в каждой внутренней точке имеет единственную касательную, то наибольшее (наименьшее) значение функции
и ее график в каждой внутренней точке имеет единственную касательную, то наибольшее (наименьшее) значение функции 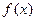 на
на 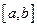 есть максимальное (минимальное) из чисел
есть максимальное (минимальное) из чисел 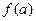 ,
,  и значений функции во всех точках максимума (минимума) этой функции.
и значений функции во всех точках максимума (минимума) этой функции.
