Нормы затрат материалов

Наименование материала	Единица измерения	Норма затрат
Сталь 40Х	Кг
Латунь Л80	Кг	1,5
Пруток 30 мм	Погм	0,5
Пластмасса	Кг

Прогнозная цена 1 погонного Прогнозная цена 1 килограмма

метра прутка стали 40Х

0,8 0,9

120 140 80 90 110

Прогнозная цена 1 килограмма Прогнозная цена 1 килограмма

Пластмассы латуни

0,7 0,6

0,4

15 20 30 40 150 200

Рис. 4. Прогнозные значения цен на материалы.

Решение:

Обозначим нечеткие числа, описывающие прогнозные цены на материалы следующим образом: 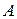– цена стали; – латуни; 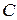–прутка; 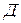– пластмассы. Тогда:

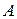=(90;90;10;20;0,9); =(150;150;0;0;0,6) 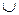(200;200;0;0;0,4); 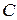=(120;140;0;0;0,8); 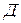=(20;30;5;10;0,7).

Затраты на материалы с учетом их норм расхода:

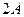=(180;180;20;40;0,9); 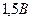=(225;225;0;0;0,6) 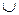(300;300;0;0;0,4);

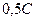=(60;70;0;0;0,8); 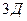=(60;90;15;30;0,7).

Прогнозная сумма материальных затрат будет представлена нечетким числом:

.

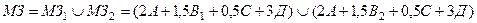Вычислим :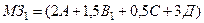

;

; ;

;

.

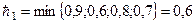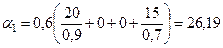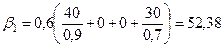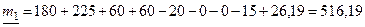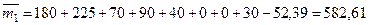Таким образом, .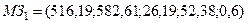

Аналогично вычислим :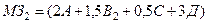

;

;

;

;

;

.

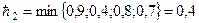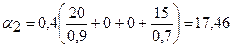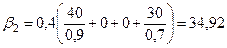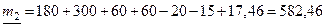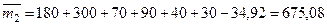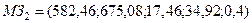Для прогнозной суммы затрат получаем следующее выражение:

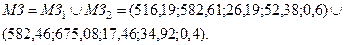
Функция принадлежности числа 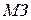представлена на рис.5.

0,6

0,4

490 516,19 582,61 675,08 710

Рис. 5. Функция принадлежности прогнозного значения

суммы затрат на материалы.

Метод построения прогнозного сценария

Метод построения прогнозного сценария основан на установлении логической последовательности состояний прогнозируемого объекта в зависимости от состояния окружающей среды во времени и рассматривает различные варианты развития данного объекта.

Как правило, каждый сценарий состоит из трех частей:

1. В первой части приводится описание существующей реальности и динамических характеристик исследуемого объекта;

2. Во второй рассматриваются возможные варианты будущего развития объекта прогнозирования;

3. В третьей приводятся конечные варианты прогнозных расчетов.

Прогнозный сценарий обычно рассматривает три варианта развития объекта прогнозирования:

· оптимистический – развитие объекта прогнозирования осуществляется в благоприятной ситуации;

· пессимистический – развитие объекта прогнозирования осуществляется в неблагоприятной ситуации;

· рабочий – развитие объекта прогнозирования осуществляется в наиболее вероятной ситуации.

В отдельных случаях в рамках прогнозного сценария может прорабатываться резервная стратегия на случай возникновения непредвиденных ситуаций.

Сценарный метод нашел широкое применение при прогнозировании и планировании быстро протекающих во времени процессов. В быстро протекающих процессах для верной оценки сложившейся ситуации и принятия решения, как правило, не хватает времени. Использование сценарного метода нейтрализует фактор внезапности и дает возможность в спокойной обстановке выявить возможные решения и оценить последствия их реализации.