Параметрические критерии

1) F-критерий Фишера-Снедекора

Многие гипотезы требуют равенства дисперсий во всех ячейках комплекса. Этот факт можно установить с помощью критерия Фишера-Снедекора.

Алгоритм метода:

1.Две случайные величины Х и Y распределены по N

2.Имеются две выборки с объёмами, соответственно п_х и п_у.

3.Требуется на уровне значимости a(0,1; 0,05; 0,01) проверить гипотезу:

Н0: D(X) = D(Y)

Н1: D(X) ¹ D(Y) или H1: D(X) < либо > D(Y)

4.Вычисляют 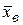и

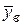
5.Находят оценк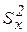и и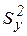

6.Вычисляют эмпирическое значение статистического критерия:

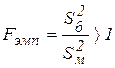
7.По таблицам находят критическое значение критерия:

F_кр = (p; f_б; f_м), где f_б = п_б – 1

f_м = п_м – 1;

р = a / 2 (для двухсторонней области)

р = a (для односторонней области)

8.Сравнивают F_эмп и F_кр:

Если F_эмп < F_кр Þ Н₀

Если F_эмп ³ F_кр Þ Н₁

2) Проверка равенства генеральных средних (случай больших выборок); z-критерий

Алгоритм метода:

1.Две случайные величины Х и Y распределены по N

2.Имеются две выборки с объёмами, соответственно п_х и п_у (> 50)

3.Требуется на уровне значимости a(0,1; 0,05; 0,01) проверить гипотезу:

Н0: М(X) = М(Y)

Н1: М(X) ¹ М(Y) или H1: М(X) < либо > М(Y)

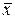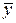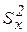4.Вычисляют и , и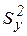

5.Вычисляют эмпирическое значение z-критерия:

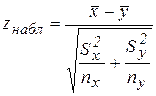
6.По таблицам функции Лапласа находим критическое значение:

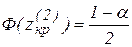для двусторонней области

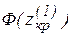= 1 - a для односторонней области

Ф(z) = 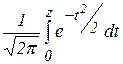- функция Лапласа

7.Сравнение z_набл и z_кр:

Для двусторонней области ½z_эмп½< z_кр⁽²⁾

Для левосторонней области z_эмп > - z_кр⁽¹⁾ Þ Н₀

Для правосторонней области z_эмп < z_кр⁽¹⁾

В противном случае Н₁

3) Сравнение малых выборок (п < 50) t-критерий Стьюдента:

1.Две случайные величины Х и Y распределены по N

2.Имеются две выборки с объёмами, соответственно п_х и п_у (> 50)

3.Требуется на уровне значимости a(0,1; 0,05; 0,01) проверить гипотезу:

Н0: М(X) = М(Y)

Н1: М(X) ¹ М(Y) или H1: М(X) < либо > М(Y)

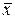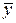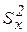4.Вычисляют и , и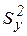

5.Вычисляют критическое значение t-критерия:

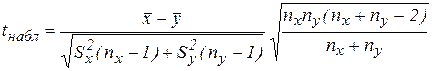
6.По таблицам распределения Стьюдента находим критическое значение t_кр(a; f), где f = n_x + n_y – 2 - ЧСС.

7.Если ½t_набл½ < t_кр Þ Н₀; в противном случае Н₁.

4) Для непарных выборок при неравенстве дисперсий (критерий Уэлча (Welch)):

t _набл. =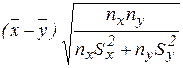

с ЧСС:

К =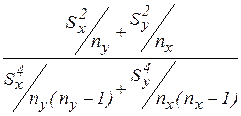

5) Для парных выборок п_х = п_у = п:

t _набл. =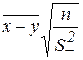

с ЧСС п – 1.

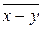– среднее для выборки, составленной из разностей парных элементов двух выборок.

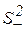– дисперсия для выборки, составленной из разностей парных элементов двух выборок.

Для парных выборок необходимо требование связанности этих выборок: контроль – эксперимент, «до – после».

Сравнение нескольких дисперсий нормальных генеральных совокупностей:

6) по выборкам различного объёма (критерий Батлетта):

х₁, х₂, …, х_k – N (генеральной совокупности)

п₁, п₂, …, п_k – объёмы выборок

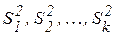– исправленные выборочные дисперсии

Требуется на уровне значимости a проверить гипотезу:

Н₀: D(х₁) = D(х₂) = … = D(х_k)

Н₁: неоднородность дисперсий

n_i – ЧСС i-ой выборки n_i = п_i – 1.

Средне взвешенная по числам степеней свободы исправленная дисперсия:

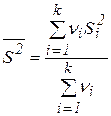n =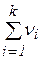

В качестве критерия для проверки Н₀ используем случайную величину В = V / С, распределённого приближённо по c² с К – 1 степенями свободы при условии, что n_i > 2, т. е. п_i ³ 4:

V = 2,303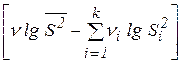

C = 1 +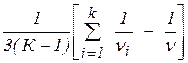

Область критерия – правосторонняя, т. е. уровень значимости:

Р [B > c_кр² (a; K – 1)] = a

Н₀ принимается, если B < c_кр² a = 0,05

Н₀ отвергается, если B > c_кр² a = 0,01

7) по выборкам одинакового объёма (критерий Кочрена):

х₁, х₂, …, х_k – N

п₁ = п₂ = …= п_k = п

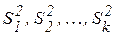
На уровне a:

Н₀: D(х₁) = D(х₂) = … = D(х_k) однородность

Н₁: неоднородность дисперсий

В качестве критерия проверки Н₀ принимают случайную величину Ст:

G_набл. =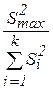

G_крит. = G_крит (a; n; к) по специальным таблицам

n = п – 1 – число степеней свободы; к – количество выборок

Правило принятия Н₀: G_набл. < G_крит. для a = 0,05

отвергания Н₀: G_набл. > G _крит. для a = 0,01