Пример выполнения работы. Решить задачу Коши:
Решить задачу Коши:

1. Решаем задачу методом Эйлера на микрокалькуляторе. В нашем случае a=2, b=3,6, поэтому шаг интегрирования будет равен

Записываем формулу (4.3) для нашей задачи
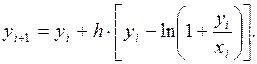
Выполняя последовательно по этой формуле расчеты с шагом 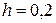 и с шагом
и с шагом 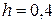 , заполняем табл. 4.2.
, заполняем табл. 4.2.
Таблица 4.2
Решение задачи Коши методом Эйлера
 | 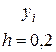 |  |  |
| 2,0 | 1,000 | 1,000 | 0,000 |
| 2,2 | 1,119 | ||
| 2,4 | 1,260 | 1,238 | 0,022 |
| 2,6 | 1,428 | ||
| 2,8 | 1,626 | 1,567 | 0,059 |
| 3,0 | 1,860 | ||
| 3,2 | 2,135 | 2,015 | 0,120 |
| 3,4 | 2,460 | ||
| 3,6 | 2,843 | 2,626 | 0,217 |
Находим максимум величин  , определяем, что локальная погрешность решения, полученного с шагом
, определяем, что локальная погрешность решения, полученного с шагом  , не превышает 0,217.
, не превышает 0,217.
2. Решаем задачу методом Рунге-Кутта на микрокалькуляторе. В нашем случае a=2, b=3,6, поэтому шаг интегрирования будет равен
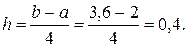
Записываем формулы (4.5), (4.6) для нашей задачи
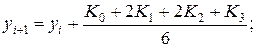
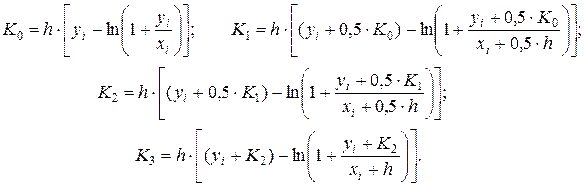
Выполняя последовательно по этим формулам расчеты с шагом 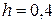 , заполняем табл. 4.3.
, заполняем табл. 4.3.
Таблица 4.3
Решение задачи Коши методом Рунге-Кутта
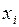 |  | 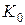 | 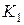 | 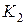 | 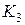 |
| 2,0 | 1,000000 | 0,237814 | 0,283092 | 0,289428 | 0,343770 |
| 2,4 | 1,287770 | 0,343287 | 0,405555 | 0,414952 | 0,491064 |
| 2,8 | 1,700330 | 0,490319 | 0,578250 | 0,592296 | 0,700948 |
| 3,2 | 2,289057 | 0,699781 | 0,825797 | 0,846849 | 1,003755 |
| 3,6 | 3,130528 |
3. Строим графики приближенных решений (рис. 4.4).
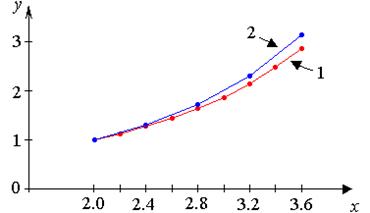
Рис. 4.4. Графики приближенных решений, полученных методом
Эйлера (кривая 1) и методом Рунге-Кутта (кривая 2)
4. Продолжаем выполнение работы в компьютерном классе. Запускаем программу Mathcad. Открываем файл Lab4.mcd. Вводим функцию, стоящую в правой части уравнения (4.1), начальное условие, правую и левую границу интегрирования

5. С помощью заложенного в файле Lab4.mcd программного блока системы Mathcad (в начале любого блока обязательно должно присутствовать слово Given)
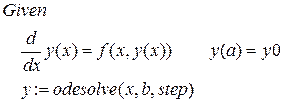
находим решение дифференциального уравнения с шагом интегрирования 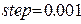 (в дальнейшем будем называть его точным решением). Выписываем полученные значения этого решения
(в дальнейшем будем называть его точным решением). Выписываем полученные значения этого решения 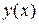 в промежуточных точках (табл. 4.4)
в промежуточных точках (табл. 4.4)
Таблица 4.4
Точное решение задачи Коши
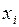 |  |
| 2,0 | 1,0000000000 |
| 2,2 | 1,1307465872 |
| 2,4 | 1,2877847424 |
| 2,6 | 1,4757530270 |
| 2,8 | 1,7003752743 |
| 3,0 | 1,9686608656 |
| 3,2 | 2,2891619457 |
| 3,4 | 2,6722961416 |
| 3,6 | 3,1307469976 |
И по этим значениям строим график точного решения (рис. 4.5)

Рис. 4.5. График точного решения, полученного с помощью компьютера
6. Используя значения табл. 4.4, вычисляем локальные абсолютные погрешности, с которыми найдены приближенные решения по методу Эйлера и Рунге-Кутта (табл. 4.5).
Таблица 4.5
Таблица погрешностей решений задачи Коши методами Эйлера и Рунге-Кутта
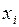 |  (точное решение) (точное решение) |  (метод Эйлера) (метод Эйлера) | 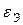 |  (метод Рунге-Кутта) (метод Рунге-Кутта) | 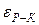 |
| 2,0 | 1,0000000000 | 1,000 | 0,0000000 | 1,000000 | 0,0000000 |
| 2,2 | 1,1307466119 | 1,119 | 0,0117466 | ||
| 2,4 | 1,2877848040 | 1,260 | 0,0277847 | 1,287770 | 0,0000147 |
| 2,6 | 1,4757531434 | 1,428 | 0,0477530 | ||
| 2,8 | 1,7003754702 | 1,626 | 0,0743753 | 1,700330 | 0,0000453 |
| 3,0 | 1,9686611750 | 1,860 | 0,1086609 | ||
| 3,2 | 2,2891624149 | 2,135 | 0,1541619 | 2,289057 | 0,0001049 |
| 3,4 | 2,6722968333 | 2,460 | 0,2122961 | ||
| 3,6 | 3,1307479958 | 2,843 | 0,2877470 | 3,130528 | 0,0002190 |
Находим максимум величин 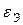 и
и 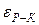 , определяем, что локальная погрешность решения методом Эйлера в точках
, определяем, что локальная погрешность решения методом Эйлера в точках 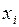 , полученного с шагом
, полученного с шагом 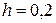 , не превышает
, не превышает
 ,
,
а локальная погрешность решения методом Рунге-Кутта, полученного с шагом 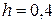 , не превышает
, не превышает
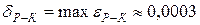 .
.
То есть даже небольшое количество точек разбиения отрезка интегрирования 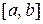 обеспечивает малую погрешность решения методом Рунге-Кутта.
обеспечивает малую погрешность решения методом Рунге-Кутта.
7. Подставив 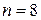 , получим с помощью компьютера решение задачи Коши методом Рунге-Кутта и, используя уже найденное решение для
, получим с помощью компьютера решение задачи Коши методом Рунге-Кутта и, используя уже найденное решение для  , определим по формуле (4.7) относительную погрешность.
, определим по формуле (4.7) относительную погрешность.
Таблица 4.6
Относительная погрешность решения методом Рунге-Кутта
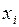 | 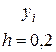 |  | 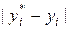 |
| 2,0 | 1,000000 | 1,000000 | 0,000 |
| 2,2 | 1,130746 | ||
| 2,4 | 1,287784 | 1,287770 | 0,000014 |
| 2,6 | 1,475751 | ||
| 2,8 | 1,700372 | 1,700330 | 0,000042 |
| 3,0 | 1,968656 | ||
| 3,2 | 2,289155 | 2,289057 | 0,000098 |
| 3,4 | 2,672286 | ||
| 3,6 | 3,130733 | 3,130528 | 0,000205 |
Находим максимум величин 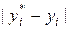 , определяем, что относительная погрешность решения, полученного с шагом
, определяем, что относительная погрешность решения, полученного с шагом 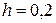 , не превышает
, не превышает
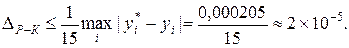
8. Все расчеты оформляются в виде отчета по лабораторной работе.
Вопросы для самоконтроля
1. Что называется обыкновенным дифференциальным уравнением? Записать в нормальной форме уравнение первого порядка.
2. Что является частным и общим решением дифференциального уравнения?
3. Как ставится задача Коши для дифференциального уравнения первого порядка? При каких условиях эта задача имеет, причем единственное, решение?
4. Каков геометрический смысл дифференциального уравнения первого порядка? Что означает решить задачу Коши с геометрической точки зрения?
5. В каком виде ищется решение задачи Коши численным методом?
6. Записать расчетную формулу метода Эйлера. Каков геометрический смысл метода Эйлера?
7. Записать расчетные формулы для метода Рунге-Кутта.
8. Записать формулы для расчета погрешности в методах Эйлера и Рунге-Кутта.
9. Привести алгоритм выбора начального шага в методе Рунге-Кутта.
