Расчет термических напряжений

При значительных скоростях нагрева в пластине могут возникать термиче­ские напряжения, превышающие допустимые для данного материала, приводящие в некоторых случаях даже к разрушению пластины.

В этом разделе получим формулы для расчета термических напряжений, возникающих при нагреве или охлажении.

Согласно литературным данным, например [9], для определения темпера­турных напряжений в бесконечно большой пластине толщиной 2d при симмет­ричном распределении температур можно воспользоваться следующим выраже­нием:

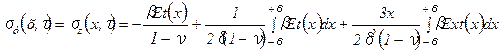, (4.1)

где s_у(х,t) и s_z(х,t) – нормальные составляющие напряжения, параллельные осям y, z, Па;

b - линейный коэффициент температурного расширения, 1/К;

Е – модуль упругости на растяжение и сжатие, Па;

v - коэффициент Пуассона;

t(x) – текущая температура, определенная выше решением (3.4).

4.1. Аналитический расчет термических напряжений при конвективном нагреве плоских тел

Без знания температурных полей и термических напряжений внутри массивного тела невозможно назна­чить рациональные энерго- и материалосберегающие тепловые и температур­ные режимы печей или других агрегатов, связанных с тепловой обработкой ма­териалов, например, сушильных установок, химических реакторов и т. п. При значительных скоростях нагрева в пластине могут возникать термиче­ские напряжения, превышающие допустимые для данного материала, приводящие в некоторых случаях даже к разрушению тела.

После подстановки в уравнение (4.1) полученное ранее температурное

Поле пластины (3.4) в безразмерном виде получим формулу для расчета относительных термических напряжений в любой точке неограниченной

пластины при ее конвективном нагреве в печи с постоянной температурой греющей среды :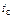

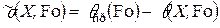, (4.2)

на поверхности при Х=1

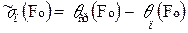= (4.3)

и в центре пластины при Х=0

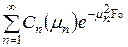= , (4.4)

где 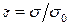— безразмерные термические напряжения, ;

s₀ = bЕDt₀/(1–n) — максимально возможные термические напряжения, Па.

Здесь относительные температуры:

в любой точке

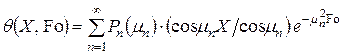, (4.5)

на поверхности

, (4.6)

в центре

(4.7)

и среднемассовая

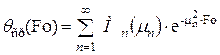,(4.8)

где 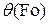=(t(τ)–t_c)/Dt₀; Dt₀= t₀– t_c; t_{0 ­} —начальная температура тела, °С;

Fо= aτ/R₀²- число Фурье;

Вi=αR₀/λ – число Био;

– тепловая амплитуда;

; ; ; ;

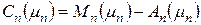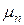– собственные числа, определяемые характеристическим уравнением:

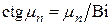. (4.9)

Решая совместно уравнения (4.3) и (4.4), можно получить формулу связи между термонапряжениями в центре и на поверхности

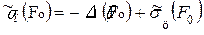, (4.10)

где относительный перепад температур получается путем вычитания из (4.6) уравнения (4.7)

(4.11)

в котором .

Из анализа уравнений (4.3), (4.4), (4.10) и (4.11) следует, что динамика изменения напряжений во времени аналогична изменению температурной разности, т.е. резко возрастают, достигая максимального значения при числах Фурье Fo_max­=0,05…0,50, а затем постепенно падают, т.е. носят колоколообразный характер.

На практике иногда важнее знать не всю динамику изменений напряжений во времени, а только их максимально возможные характерные величины. Целью данного раздела является аналитическое определение указанных величин.

Дифференцируя уравнения (4.3), (4.4) и (4.11) по времени, приравнивая производную нулю и используя два члена суммы ряда, получим формулы для расчёта максимальных времен Фурье:

для максимального термического напряжения на поверхности

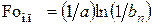, (4.12)

перепада температур

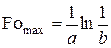(4.13)

и термонапряжения в центре

, (4.14)

где ; ; ; ; .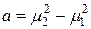

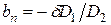Здесь и далее под понимается амплитуда .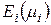

Подставляя Fо_mах из (4.13) в уравнение (4.11), получим максимальный перепад температур с учётом двух членов ряда:

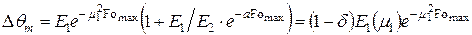. (4.15)

При выводе (4.15) было учтено, что согласно уравнению (4.13) .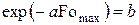

По аналогии подставляя 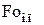в уравнение (4.3), получим максимальное термическое напряжение на поверхности

(4.16)

и после подстановки (4.14) в (4.4) — максимальное напряжение в центре пластины

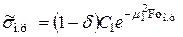. (4.17)