Задание на курсовую работу. Курсовая работа

Курсовая работа

По дисциплине «Радиотехнические цепи и сигналы»

Вариант 2

Спектральный анализ сигналов

Выполнил: студент 3-го курса,

Факультета РТС,

Гр.

Руководитель: Исаков В.Н.

Москва 2005

Содержание:

Задание на курсовую работу 3

Спектральный анализ непериодического сигнала. 4

Спектральный анализ периодического сигнала. 7

Спектральный анализ одиночного радиоимпульса. 9

Спектральный анализ периодической последовательности

Радиоимпульсов. 12

Корреляционный анализ непериодического сигнала. 13

Спектральный анализ линейной цепи. 15

Список литературы 17

Задание на курсовую работу

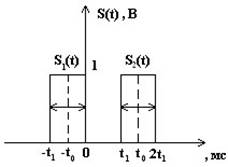
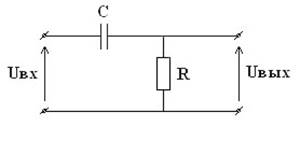
Рис. 1. Заданный сигналРис.2. Заданная цепь

В курсовой работе требуется:

1.Определить амплитудный спектр видеоимпульса и построить его график.

2.Определить амплитудный спектр периодической последовательности видеоимпульсов со скважностью Q=5, построить его график.

3.Определить амплитудный спектр радиоимпульса, построить его график.

4.Определить амплитудный спектр периодической последовательности радиоимпульсов, построить его график.

5.Определить автокорреляционную функцию заданного видеоимпульса, построить её график.

6.Записать выражение для спектра видеосигнала на выходе цепи заданного вида.

1. Спектральный анализ непериодического сигнала.

Аналитическое описание заданного сигнала:

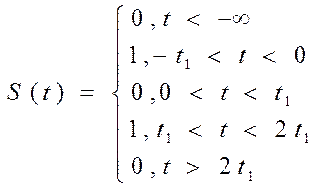
Длительность прямоугольных импульсов, составляющих сигнал:

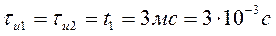
Представим пачку заданных видеоимпульсов двумя одиночными видеоимпульсами (рис.3 а,б)

Рис.3

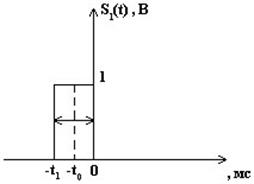
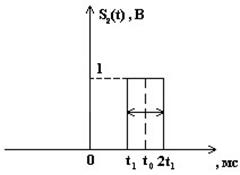
а) б)

, ,

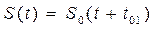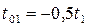
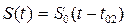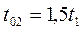
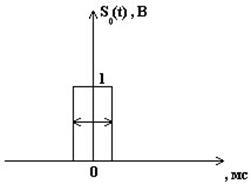
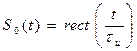- одиночный видеоимпульс с амплитудой V₀=1В и длительностью τ_и=3мс, относительно которого рассматриваются импульсы, составляющие сигнал (рис.3 в).

в)

Таким образом, в аналитическом виде заданный сигнал (рис.1) будет иметь вид:

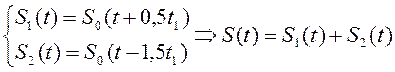
Спектральная плотность определяется преобразованием Фурье:

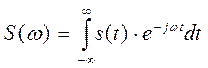
Функция S(ω) в общем случае является комплексной:

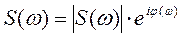
S(ω) – амплитудный спектр

φ(ω) – фазовый спектр

Задачу определения спектральной плотности заданного сигнала можно упростить, воспользовавшись свойствами преобразования Фурье:

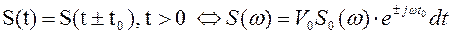,(1)

V₀ – амплитуда.

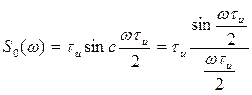, (2) – для прямоугольного видеоимпульса

Согласно (1) и (2) получаем следующие спектральные плотности для видеоимпульсов, составляющих сигнал (τ_и=t₁ ,V₀=1):

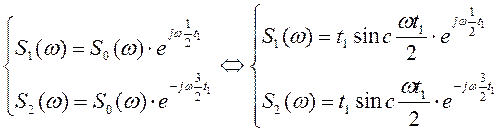
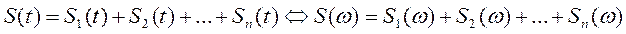
Таким образом, спектральная плотность заданного сигнала (рис.1):

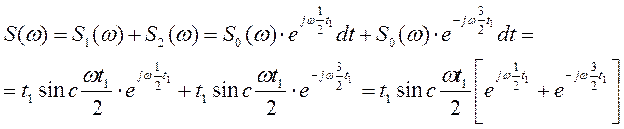
Определим амплитудный спектр сигнала:

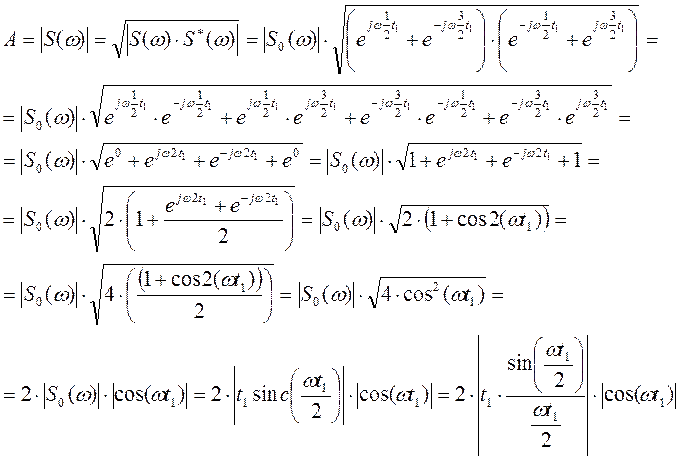при ω=2πf

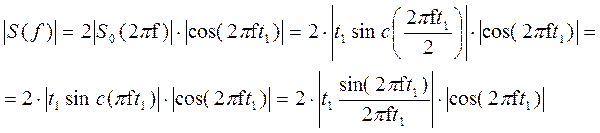
Временная диаграмма заданного сигнала представлена на рис.4.

Амплитуда видеоимпульсов, составляющих сигнал V₀=1В и длительность τ_и=t₁=3мс.

График амплитудного спектра заданного сигнала представлен на рис.5.

2.Спектральный анализ периодического сигнала.

Спектральный анализ периодических сигналов основан на разложении временной функции, описывающей сигнал, с периодом T и частотой ω₁=2π/T, по ортогональной системе тригонометрических функций (ряд Фурье для периодической последовательности):

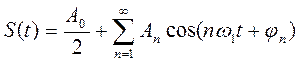, (3) ;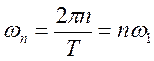

Совокупность амплитуд {A_n} определяет амплитудный спектр, а совокупность начальных фаз {φ_n} – фазовый спектр сигнала.

При определении амплитудного спектра периодических сигналов полезно использовать следующее равенство

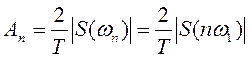, (4)

которое определяет взаимосвязь между спектрами периодических и непериодических сигналов.

Спектры периодических сигналов являются дискретными и линейчатыми, интервал дискретизации по частоте равен частоте сигнала ω₁.

Определим период T заданного сигнала получаемого периодическим повторением прямоугольного видеоимпульса (рис.) по формуле:

,

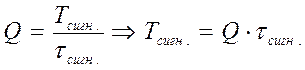где Q=5 – заданная скважность, τ_сигн.=3τ_и= 3t₁

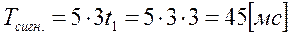
Аналитическое выражение для полученного сигнала:

,

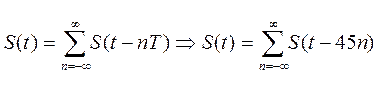где S(t) – заданный сигнал

Преобразуем круговую частоту ω₁ в f1 (ω₁ [рад/с] => f₁[Гц])

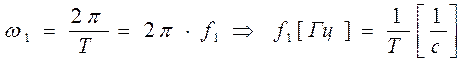
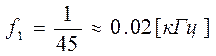
f₁– интервал дискретизации по частоте.

По формуле (4) определим амплитудный спектр периодической последовательности заданного сигнала:

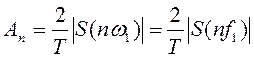
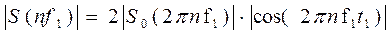– из пункта 1 курсовой работы

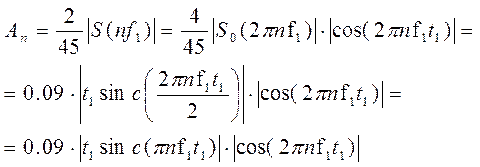
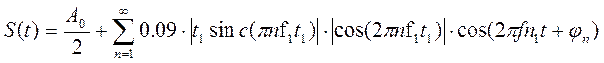
Временная диаграмма периодической последовательности заданного сигнала и график её амплитудного спектра представлены на рис.6 и 7.