Методические указания по выполнению задания 2

В Excel для вычисления значений плотности вероятности, изменяющейся по нормальному закону, применяют фун­кцию НОРМРАСП.

Функция НОРМРАСП вычисляет значения плотности вероятности нормальной функции рас­пределения для указанного среднего значения и стандартного отклонения.

Функция имеет параметры НОРМРАСП (х; среднее; стандартное откл; интегральная).

Здесь:

х – ряд значений случайной величины, для которой строится распределение;

среднее - среднее арифметическое (математическое ожидание);

стандартное откл — стандартное отклонение распределения

( среднеквадратичное отклонение);

интегральная — логическое значение, определяющее форму функции. Если интегральная имеет значение истина(1), то функция НОРМРАСП возвращает интег­ральную функцию распределения; если этот аргумент имеет значение ложь(0), то вычисляется значение функции плотности вероятности нормального распределения.

Рассмотрим пример использования функции НОРМРАСП для построения кривой нормального распределения.

Пусть нам будет задано: среднее арифметическое (или математическое ожидание) М = 24,3 и среднеквадратичное отклонение 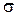= 1,5.

Решение

В ячейку А1 вводим символ случайной величины - х, а в ячейку В1- символ фун­кции плотности вероятности - f(x).

Вычисляем диапазон изменения аргумента х по правилу трех сигм, т.е. минимальное значение вычисляем по формуле: М -3* 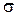= 19,8, а максимальное значение по формуле М + 3* 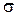= 28,8.

Вводим в диапазон А2:А21 значе­ния аргумента х от 19,8 до 28,8 с шагом 0,5. Для этого в ячейку А2 вводим левую границу диапазона (19,8), а в ячейку A3 левую границу плюс шаг (20,3). Выделяем блок А2:АЗ. Затем за правый нижний угол протягиваем мышью до ячейки А21 (при нажатой левой кнопке).

Устанавливаем табличный курсор в ячейку В2 и для получения значения веро­ятности воспользуемся специальной функцией - нажимаем на панели инстру­ментов кнопку Вставка функции- (fx).

В появившемся диалоговом окне Мастер функций - шаг 1 из 2 слева в поле Категория указаны виды функций. Выбираем Статистическая. Справа в поле Функция выбира­ем функцию НОРМРАСП. Нажимаем на кнопку ОК.

Появляется диалоговое окно НОРМРАСП. В рабочее поле х вводим значение х, для которого строится распределение (в примере адрес ячейки А2 щелчком мыши на этой ячейке). В рабочее поле Среднеевводим с клавиатуры значение математиче­ского ожидания М (в примере — 24,3). В рабочее поле Стандартное откл вводим с клавиатуры значение среднеквадратического отклонения 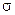(в примере — 1,5). В ра­бочее поле Интегральный вводим с клавиатуры вид функции распределения — ин­тегральная или весовая(в примере — 0). Нажимаем на кнопку ОК.

В ячейке В2 появляется значение вероятности р = 0,002955.

Указателем мыши за правый нижний угол табличного курсора протягиванием (при нажатой левой кнопке мыши) из ячейки В2 до В21копируем функцию НОРМРАСП в диапазон ВЗ: В21.

По полученным данным строим искомую диаграмму нормальной функции рас­пределения. Щелчком указателя мыши на кнопке на панели инструментов вызы­ваем Мастер диаграмм. В появившемся диалоговом окне выбираем тип диаграммы График, вид — левый верхний. После нажатия кнопки Далееуказываем диапазон данных — В1:В21 (с помощью мыши). Проверяем положение переключателя Ряды в: столбцах. Выбираем вкладку Ряд и с помощью мыши вводим диапазон подписей оси X: А2:А21. Нажав на кнопку Далее, вводим названия осей X и У: х и f(x), соот­ветственно. Нажимаем на кнопку Готово. Получаем график нормальной функции распределения плотности вероятности (рисунок 2).

Решение:

Исходные данные

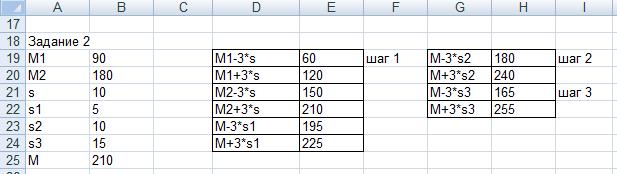
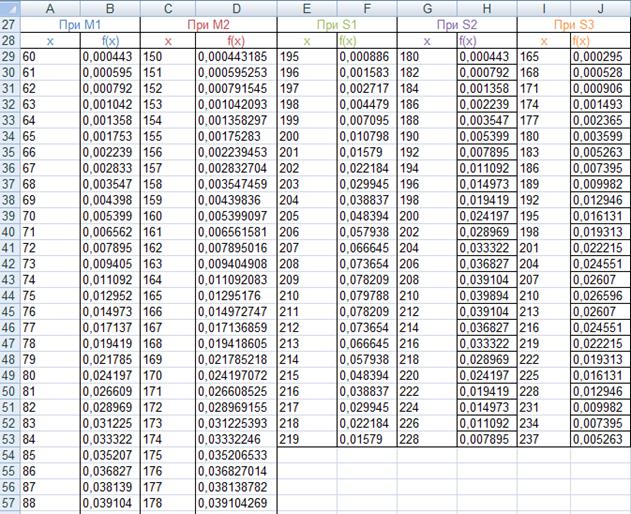
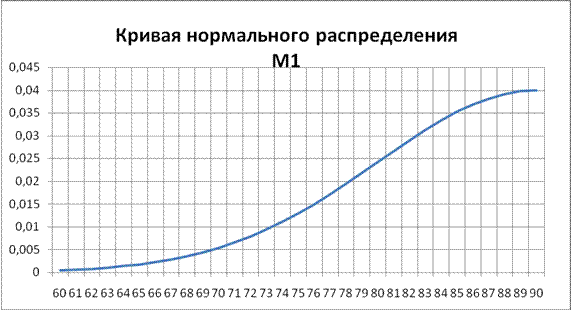
Рисунок 2 – Кривая нормального распределение М1

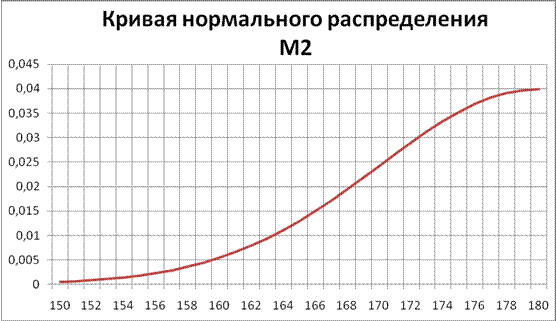
Рисунок 3 – Кривая нормального распределение М2

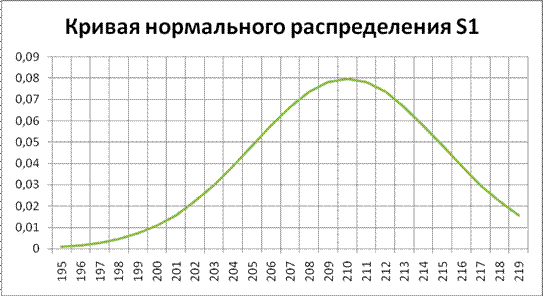
Рисунок 4 – Кривая нормального распределение S1

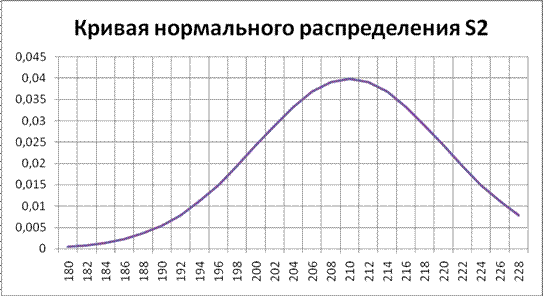
Рисунок 5 – Кривая нормального распределение S2

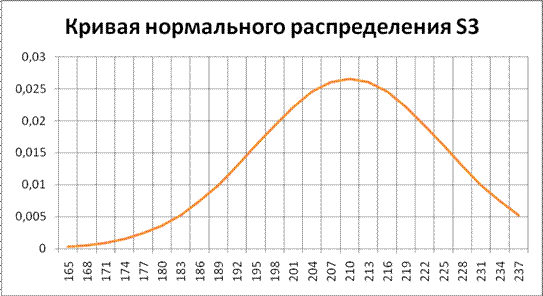
Рисунок 6 – Кривая нормального распределение S3

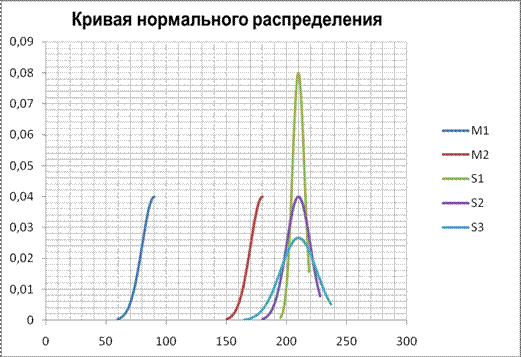
Рисунок 7 - График нормальной функции распределения

плотности вероятности для рассматриваемого примера