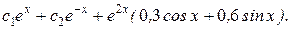Линейные неоднородные дифференциальные уравнения второго

Порядка (ЛНДУ)

Так называются уравнения вида

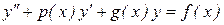, (8.22)

где p(x), g(x), f(x) – заданные, непрерывные на (a,b) функции.

Соответствующее ему уравнение (с нулевой правой частью)

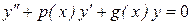(8.23)

называется однородным уравнением.

Теорема (о структуре общего решения ЛНДУ). Общее решение уравнения 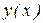(8.22) представляется суммой общего решения 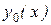соответствующего ему однородного уравнения (8.23) и частного решения 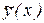неоднородного уравнения (8.22)

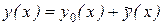. (8.24)

Доказательство. Так как 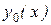- общее решение однородного уравнения (8.23), а 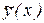- частное решение неоднородного уравнения (8.22), то 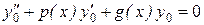и .

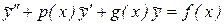В таком случае

+ ( .

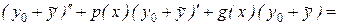
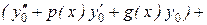
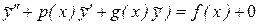А это означает, что функция 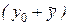является решением уравнения (8.22). Теперь необходимо показать, что функция

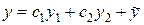(8.25)

является общим решением уравнения (8.22). Убедимся, что из решения (8.25)

можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям

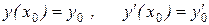, (8.26)

Подставляем данные условия в решение (8.25), получим систему уравнений

,

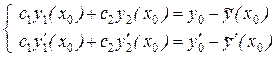относительно неизвестных с₁ и с₂.

Определителем этой системы

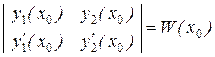
равен значению вронскиана в точке х = х₀ . Но так как 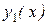и 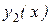являются линейно независимыми на (a,b) , то 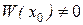. А это означает, что система (8.16) имеет единственное решение: , .

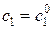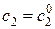Решение 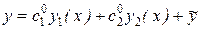является единственным частным решением уравнения (8.22), удовлетворяющим начальным условиям (8.26). Теорема доказана.

Метод вариации произвольных постоянных

Рассмотрим ЛНДУ (8.22). Его общее решение представляется суммой общего решения у₀ однородного уравнения (8.23) и частного решения 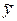неоднородного уравнения (8.22). Если известно общее решение у₀ однородного уравнения, то частное решение 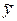можно найти методом вариации произвольных постоянных, сущность которого заключается в следующем. Пусть 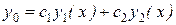- общее решение однородного уравнения. Заменим в этом выражении постоянные с₁ и с₂ неизвестными функциями с₁(х) и с₂(х) так, чтобы 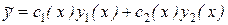было бы решением уравнения (8.22). Найдём производную

.

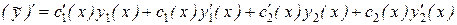Подберём функции с₁(х) и с₂(х) так, чтобы

.

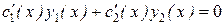Тогда ,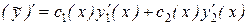

.

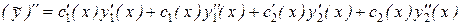Подставляя выражения 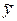, 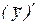и 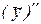в уравнение (8.22), получим

+

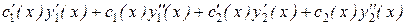+ р(х)[ 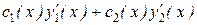] + q(x) [ 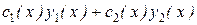] = f(x),

bли с₁(х)∙[ ] +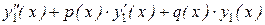

+ с₂(х)∙[ ] + /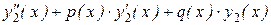

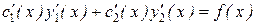Так как 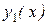и 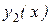- решения уравнения (8.23), то выражения в квадратных скобках равны нулю, то

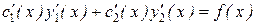. (8.27)

Таким образом, функция 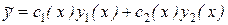будет частным решением 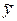уравнения (8.22), если функции с₁(х) и с₂(х) удовлетворяют системе

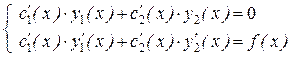, (8.28)

Определитель этой системы – вронскиан 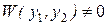, так как функци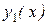и и 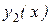линейно независимы. Поэтому система (8.28) имеет единственное решение: 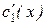и 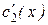. Интегрируя эти функции, находим с₁(х) и с₂(х), в результате выражение 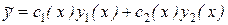является частным решением неоднородного уравнения (8.22).

ЛНДУ второго порядка с постоянными коэффициентами

Рассмотрим дифференциальное уравнение

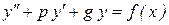, (8.29)

где p и g постоянные величины, а f(x) – заданная функция.

Согласно теореме о структуре общего решения ЛНДУ оно представляется суммой общего решения у₀ соответствующего однородного уравнения и частного решения 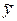неоднородного уравнения. Общее решение однородного уравнения с постоянными коэффициентами рассмотрено раннее в соответствующем разделе.

Что касается определения частного решения неоднородного уравнения с постоянными коэффициентами, то оно может быть определено с помощью метода вариации произвольных постоянных, описанного в предыдущем разделе. Однако если в правой части уравнения (8.29) - многочлен, либо показательная функция, либо тригонометрическая функция sinβx или cos βx, либо линейная комбинация перечисленных функций, то частное решение может быть найдено методом неопределённых коэффициентов, не содержащим процедуру интегрирования. Общий подход здесь таков: частное решение неоднородного уравнения, как правило, ищется в том же виде, какова его правая часть (то есть, функция f(x)). Однако, за этим “как правило” кроются многочисленные исключения.

Рассмотрим различные виды правых частей уравнения (8.29)

1. Если правая часть уравнения есть многочлен степени n f(x)=P_n(x) ) и x = 0 не является корнем характеристического уравнения, то частное решение так же следует искать в виде многочлена степени n 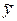(x)=Q_n(x). Если же число x = 0 является корнем характеристического уравнения кратности r, то частное решение следует искать в виде 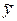(x)=x^r Q_n(x).

2. Если правая часть уравнения имеет вид 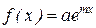и число m не является корнем характеристического уравнения, то частное решение следует искать в виде 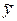(x)=Ае^mx. Если же m является корнем характеристического уравнения кратности r , то 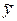(x)=А x^rе^mx.

3. Если правая часть уравнения имеет вид 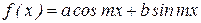и число m не является корнем характеристического уравнения, то частное решение следует искать в виде 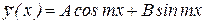. Если же m является корнем характеристического уравнения кратности r , то частное решение следует искать в виде 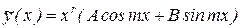. Даже в случае, когда правая часть уравнения содержит только синус, либо только косинус, частное решение все равно следует искать в виде комбинации и синуса и косинуса.

4. Если правая часть уравнения есть сумма, или произведение функций, рассмотренных выше, то частное решение следует искать в виде суммы, или произведения, соответствующих частных решений.

Пример 1. Решить задачу Коши 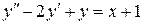, y(0) = 2, .

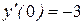Решение. Сначала найдем общее решение однородного уравнения

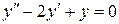. Его характеристическое уравнение 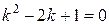имеет корни k₁ = k₂ = 1, поэтому общее решение однородного уравнения имеет вид 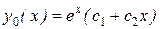. Правая часть неоднородного уравнения есть многочлен первой степени f(x)=P₁(x) = x + 1. Поскольку ноль не является корнем характеристического уравнения, то частное решение неоднородного уравнения так же будем искать в виде многочлена первой степени 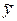(x)= Q₁(x) = Ax + B. Подберем константы А и В так, чтобы функция 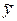удовлетворяла неоднородному уравнению. Для этого подставим функцию 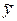(x)=Q₁(x) = Ax + B и ее производные 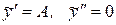 в уравнение 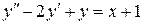, получим

-2 А + А x + B = х + 1 или Ax + (-2 A + B) = x + 1.

Последнее равенство должно выполняться при всех значениях х, что возможно лишь в том случае, когда равны коэффициенты при одинаковых степенях х в его левой и правой частях. Приравнивая соответствующие коэффициенты, получим систему линейных уравнений для определения величин А и В

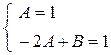
Отсюда А = 1, В = 3 и, значит, частным решением неоднородного уравнения является функция 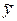(x)= x + 3. Общее решение уравнения имеет вид

y(x) = y₀(x) +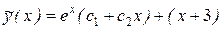

Теперь подберем константы c₁ и c₂ так, чтобы эта функция удовлетворяла заданным начальным условиям. Поскольку y(0) = 2, 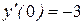то, подставив в функцию 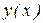и в ее производную 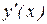заданные начальные условия, получим систему уравнений для определения постоянных c₁ и c₂

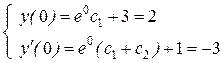
Отсюда c₁ = -1 и c₂ = -3. Значит, решением задачи является функция

.

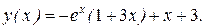Пример 2. Найти общее решение уравнения .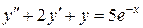

Решение. Корни характеристического уравнения 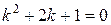k₁ = k₂ = -1 равны между собой, поэтому общее решение однородного уравнения имеет вид 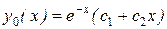. Правая часть уравнения есть функция типа ae^mx со значением m = -1, которое является корнем характеристического уравнения кратности два m = k₁ = k₂ = -1 . Поэтому, частное решение уравнения будем искать в виде 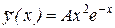. Найдем производные этой функции

,

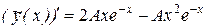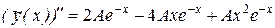
и подставим эти производные и саму функцию в исходное уравнение

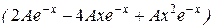+2( ,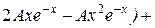

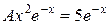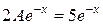
Последнее равенство возможно лишь в том случае, когда A = 5/2. Таким образом, частным решением уравнения является функция 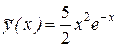, а его общее решение имеет вид y(x) = y₀(x) +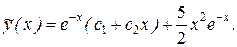

Пример 3. Найти общее решение уравнения .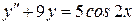

Решение. Корни характеристического уравнения 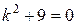равны 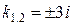( α = 0, β = 3), поэтому общее решение однородного уравнения имеет вид 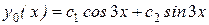. Правая часть нашего уравнения есть комбинация синуса и косинуса 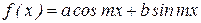при a = 5, b = 0 и m = 2.

Так как число 2i не является корнем характеристического уравнения, то частное решение уравнения будем искать в виде 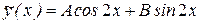. Найдем производные этой функции

,

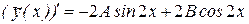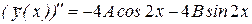
и подставим их вместе с функцией в исходное уравнение

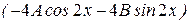+ 9 ∙ = ,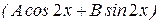

= .

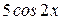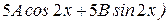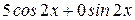Последнее равенство возможно лишь в том случае, когда A = 1 и B = 0. Значит, частным решением уравнения является функция 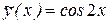, а его общее решение имеет вид

y(x) = y₀(x) +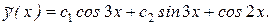

Пример 4. Найти общее решение уравнения .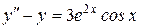

Решение. Здесь характеристическое уравнение 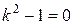имеет корни 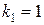, 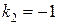. Общее решение однородного уравнения таково: 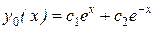. В правой части исходного уравнения – произведение показательной и тригонометрической функций. Число 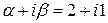не является корнем характеристического уравнения, поэтому частное решение ищем в виде 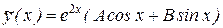. Дифференцируя и подставляя в уравнение, получим

.

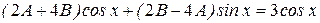Приравнивая коэффициенты при cosx и sinx, находим

, ,

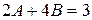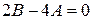откуда A=3/10, B = 3/5. Таким образом, частное и общее решения соответственно: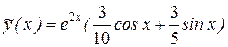

и y(x) = 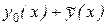=