Вводные понятия и определения. элементы
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ
ОДНОЙ ПЕРЕМЕННОЙ.
Учебное пособие для студентов
заочной формы обучения
МАГНИТОГОРСК
ВВОДНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ. ЭЛЕМЕНТЫ
ТЕОРИИ ЛОГИКИ.
Приступая к изучению математического анализа, студент уже имеет представление о понятии множеств, среди которых выделяют такие, как числовые поля. Напомним обозначения числовых множеств: 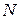 - множество натуральных чисел;
- множество натуральных чисел; 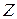 - множество целых чисел (кольцо целых чисел);
- множество целых чисел (кольцо целых чисел); 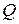 - мно -жество рациональных чисел (поле рациональных чисел);
- мно -жество рациональных чисел (поле рациональных чисел); 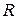 - множество действительных чисел (основное числовое поле);
- множество действительных чисел (основное числовое поле);
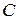 - множество комплексных чисел. Между всеми этими множествами существуют соответствующие соотношения:
- множество комплексных чисел. Между всеми этими множествами существуют соответствующие соотношения:
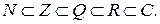
Важную роль в математическом анализе играет понятие ме- ры близости элементов различных множеств (понятие нормы или, связанного с ней, понятия метрики). Для числовых мно -жеств этой мерой является абсолютная величина или модуль.
ОПРЕДЕЛЕНИЕ . Абсолютной величиной (модулем) числа 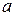 называется само число
называется само число 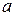 , если
, если 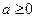 , и число
, и число 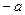 , если
, если 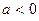 .
.
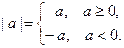
Абсолютная величина числа обладает следующими свой- ствами, которые часто используются в различных областях математики
1). 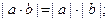 2).
2). 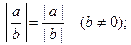
3). 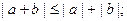 4).
4). 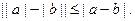
ЗАМЕЧАНИЕ. Для комплексного числа 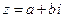 модуль равен
модуль равен 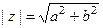 , и для него все свойства сохраняются.
, и для него все свойства сохраняются.
Действительные числа изображаются точками числовой прямой. На некоторой прямой (будем считать её располо -женной горизонтально) выберем положительное направление, начало отсчёта О и единицу масштаба  .
.
О 1 М
Для изображения положительного числа 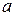 возьмём на нашей прямой справа от точки О мочку М на расстоянии ( в принятом масштабе), равном данному числу
возьмём на нашей прямой справа от точки О мочку М на расстоянии ( в принятом масштабе), равном данному числу 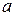 ; для изобра -жения отрицательного числа
; для изобра -жения отрицательного числа 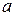 возьмём точку слева от на -чала отсчёта О на расстоянии, равном
возьмём точку слева от на -чала отсчёта О на расстоянии, равном 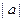 ; числу
; числу 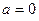 бу -дет отвечать точка O - начало отсчёта. Таким образом мы устанавливаем взаимно однозначное соответствие между все- ми точками прямой и множеством действительных чисел: каж -дое действительное число будет изображено одной опреде -лённой точкой прямой, а каждая точка прямой является изо -бражением одного определённого действительного числа. В дальнейшем мы будем обозначать одним и тем же символом
бу -дет отвечать точка O - начало отсчёта. Таким образом мы устанавливаем взаимно однозначное соответствие между все- ми точками прямой и множеством действительных чисел: каж -дое действительное число будет изображено одной опреде -лённой точкой прямой, а каждая точка прямой является изо -бражением одного определённого действительного числа. В дальнейшем мы будем обозначать одним и тем же символом 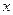 и действительное число
и действительное число 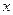 и точку
и точку 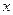 числовой оси.
числовой оси.
Множество всех действительных чисел 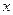 , удовлетворяю-щих неравенству
, удовлетворяю-щих неравенству 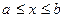 , где
, где 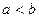 , называется отрезком (сегментом) и обозначается
, называется отрезком (сегментом) и обозначается 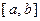 . Интервалом
. Интервалом 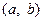 назы -вается множество всех действительных чисел
назы -вается множество всех действительных чисел 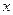 , удовлетво –ряющих неравенству
, удовлетво –ряющих неравенству 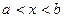 . Аналогично определяются понятия полуинтервалов
. Аналогично определяются понятия полуинтервалов 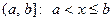 и
и 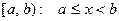
Мы будем рассматривать также бесконечные интервалы, введя несобственные точки (числа) 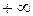 и
и 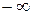 , т.е.
, т.е. 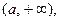
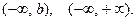
Пусть 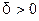 .
.  - окрестностью точки
- окрестностью точки 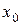 называется интер- вал
называется интер- вал 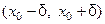 . Проколотой
. Проколотой  - окрестностью точки
- окрестностью точки  называется
называется 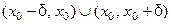 .
.
ОПРЕДЕЛЕНИЕ. Множество 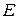 действительных чисел называется ограниченным сверху (снизу), если существует число
действительных чисел называется ограниченным сверху (снизу), если существует число 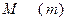 такое, что для всякого числа
такое, что для всякого числа 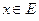 выпол- няется неравенство
выпол- няется неравенство 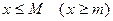 .
.
Множество 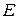 называется ограниченным, если для всякого
называется ограниченным, если для всякого 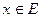 выполняется неравенство
выполняется неравенство 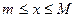 (т.е.
(т.е. 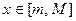 ). Число
). Число 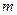 называется нижней гранью множества
называется нижней гранью множества 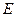 , а
, а 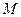 - верхней гранью.
- верхней гранью.
Исходя из свойств действительных чисел, можно утверж -дать, что среди всех нижних граней найдётся наибольшая, а среди всех верхних граней - наименьшая.. Их обозначают 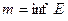 или
или 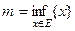 - точная нижняя грань ( infiinum - наинизший );
- точная нижняя грань ( infiinum - наинизший ); 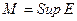 или
или 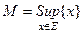 - точная верхняя грань множества
- точная верхняя грань множества 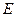 (supremum - наивысший).
(supremum - наивысший).
В дальнейшем для сокращения записи и для построения определений мы будем пользоваться некоторыми логическими символами и отношениями.
Квантор существования - 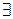 - соответствует словам «сущес- твует», «найдётся». Квантор общности -
- соответствует словам «сущес- твует», «найдётся». Квантор общности - 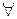 - соответствует словам «для всякого», «для любого», «для каждого», «для всех».
- соответствует словам «для всякого», «для любого», «для каждого», «для всех».
Будем называть высказыванием всякое повествовательное предложение, в отношении которого имеет смысл утверждать, истинно оно или ложно. Высказывания условимся обозначать 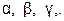 .
.
Импликация 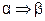 (если
(если 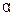 , то
, то 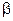 ) или (
) или ( 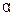 влечёт
влечёт 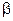 ) означает высказывание, которое ложно в том или только в том случае, когда
) означает высказывание, которое ложно в том или только в том случае, когда 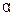 истинно, а
истинно, а 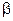 - ложно.
- ложно.
Эквивалентность - 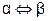 (
( 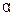 тогда и только тогда, когда
тогда и только тогда, когда 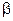 ) означает логическую равносильность высказываний
) означает логическую равносильность высказываний 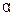 и
и 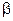 .
.
Конъюнкция 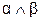 означает : высказывание «
означает : высказывание « 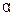 и
и 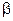 » считается истинным тогда и только тогда, когда оба высказывания
» считается истинным тогда и только тогда, когда оба высказывания 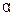 и
и 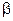 истинны.
истинны.
Дизъюнкция 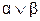 означает высказывание
означает высказывание 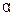 или
или 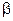 считается истинным высказыванием тогда и только тогда, когда истинно хотя бы одно из данных высказываний.
считается истинным высказыванием тогда и только тогда, когда истинно хотя бы одно из данных высказываний.
Отрицание - 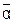 означает «не
означает «не 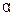 » - истинно, если
» - истинно, если 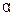 ложно и, наоборот, ложно, если
ложно и, наоборот, ложно, если 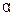 истинно.
истинно.
Отрицание некоторого свойства, содержащего кванторы 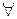 и
и 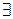 , получается заменой каждого квантора на двойственный и заменой «свойства» на его отрицание. При этом, если
, получается заменой каждого квантора на двойственный и заменой «свойства» на его отрицание. При этом, если 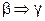 , то
, то 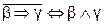 .
.
Необходимое и достаточное условия: всякое высказывание 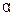 , из которого следует
, из которого следует 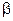 , называется достаточным условием для
, называется достаточным условием для 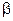 . Высказывание
. Высказывание 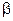 в этом случае называется необхо -димым для высказывания
в этом случае называется необхо -димым для высказывания 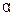 .
.
Если высказывания 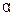 и
и 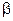 таковы, что из каждого из них вытекает другое, т.е.
таковы, что из каждого из них вытекает другое, т.е. 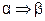 и
и 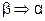 , то говорят, что каждое из высказываний
, то говорят, что каждое из высказываний 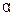 и
и 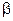 является необходимым и доста -точным для другого и пишут
является необходимым и доста -точным для другого и пишут 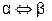 .
.
§ 2. ПОСЛЕДОВАТЕЛЬНОСТЬ, ПРЕДЕЛ ПОСЛЕДО –
ВАТЕЛЬНОСТИ.
2.1 Числовые последовательности и операции с ними.
ОПРЕДЕЛЕНИЕ 1. Если каждому числу 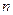 натурального ряда чисел: 1, 2, ….,
натурального ряда чисел: 1, 2, …., 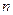 , … , по определённому закону, ста - вится в соответствие некоторое действительное число
, … , по определённому закону, ста - вится в соответствие некоторое действительное число 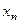 , то множество занумерованных действительных чисел
, то множество занумерованных действительных чисел
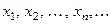 (1)
(1)
называется числовой последовательностью или просто последовательностью.
Число 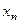 называется общим членом последовательности,
называется общим членом последовательности, 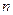 - порядковым номером последовательности. Зная порядко- вый номер и общий член последовательности, можем указать любой член последовательности. Сокращённо последователь -ность (1) обозначается символом
- порядковым номером последовательности. Зная порядко- вый номер и общий член последовательности, можем указать любой член последовательности. Сокращённо последователь -ность (1) обозначается символом  . Например символом
. Например символом
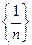 обозначается последовательность:
обозначается последовательность: 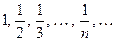 и таким же образом, по общему члену последовательности можно определить любой член последовательности.
и таким же образом, по общему члену последовательности можно определить любой член последовательности.
Введём понятие арифметических операций над числовыми последовательностями. Пусть даны произвольные последова-тельности  и
и 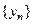 . Суммой этих последовательностей называется последовательность
. Суммой этих последовательностей называется последовательность 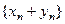 , разностью - после- довательность
, разностью - после- довательность 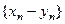 , произведением - последовательность
, произведением - последовательность 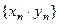 и частным - последовательность
и частным - последовательность 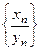 . ( При определении операции
. ( При определении операции 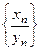 необходимо требовать , чтобы все элементы последовательности
необходимо требовать , чтобы все элементы последовательности 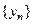 были отличны от нуля.
были отличны от нуля.
ОРПЕДЕЛЕНИЕ 2. Последовательность  называется ограниченной сверху (снизу) если существует такое действи- тельное число
называется ограниченной сверху (снизу) если существует такое действи- тельное число 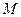 (число
(число 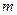 ), что каждый элемент после -довательности
), что каждый элемент после -довательности  удовлетворяет неравенству
удовлетворяет неравенству
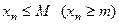 . (1)
. (1)
При этом число 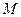 (число
(число 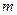 ) называется верхней (нижней ) гранью последовательности
) называется верхней (нижней ) гранью последовательности  , а условия (1) называются условиями ограниченности последовательности сверху (снизу).
, а условия (1) называются условиями ограниченности последовательности сверху (снизу).
ОПРЕДЕЛЕНИЕ 3. Последовательность  называется ограниченной, если она ограничена сверху и снизу, т.е. если существует число
называется ограниченной, если она ограничена сверху и снизу, т.е. если существует число  , такое что
, такое что 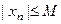 для всех
для всех 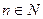 .
.
Например, последовательность 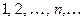 ограничена снизу, но неограниченна сверху;
ограничена снизу, но неограниченна сверху;
последовательность 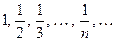 ограничена сверху числом 1, а снизу числом 0, т.е. просто ограничена;
ограничена сверху числом 1, а снизу числом 0, т.е. просто ограничена;
последовательность 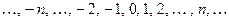 не ограничена ни сверху, ни снизу.
не ограничена ни сверху, ни снизу.
2.2. Бесконечно большие и бесконечно малые последовательности.
О п р е д е л е н и е 1. Последовательность  называется бесконечно большой, если для любого положительного числа
называется бесконечно большой, если для любого положительного числа 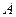 существует номер
существует номер 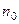 , начиная с которого (т.е. для всех
, начиная с которого (т.е. для всех 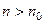 ) выполняется неравенство
) выполняется неравенство 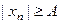 . (2)
. (2)
Например, последовательность 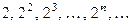 являет-ся бесконечно большой, а неограниченная последовательность
являет-ся бесконечно большой, а неограниченная последовательность 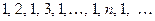 не является бесконечно большой, так как для сколь угодно больших номеров
не является бесконечно большой, так как для сколь угодно больших номеров 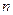 существуют элементы равные 1 и невозможно выполнение неравенства (2).
существуют элементы равные 1 и невозможно выполнение неравенства (2).
О п р е д е л е н и е «. Последовательность 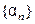 называется бесконечно малой, если для любого положительного числа
называется бесконечно малой, если для любого положительного числа 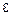 существует номер
существует номер 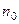 , начиная с которого все элементы последовательности
, начиная с которого все элементы последовательности 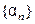 удовлетворяют неравенству
удовлетворяют неравенству 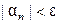 .
.
Например, последовательность 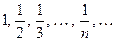 является бесконечно малой. В самом деле, для произвольного
является бесконечно малой. В самом деле, для произвольного 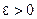 существует номер
существует номер 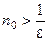 , начиная с которого (для всех
, начиная с которого (для всех 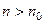 ) выполняется неравенство:
) выполняется неравенство: 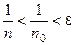 .
.
Основные свойства бесконечно малых последователь- ностей.
1 Сумма или разность бесконечно малых последова- тельностей является бесконечно малой последова -тельностью. (более того, как следствие, алгебраическая сумма (т.е. сумма или разность) любого конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью).
2 Бесконечно малая последовательность - ограничена.
3 Произведение ограниченной последовательности на бесконечно малую - бесконечно малая последователь- ность. ( в частности, при умножении бесконечно малой последовательности на любое число получим бесконеч- но малую последовательность).
4 Произведение двух бесконечно малых последователь- ностей - бесконечно малая последовательность (как следствие, произведение любого конечного числа бес- конечно малых последовательностей является бесконеч- но малой последовательностью).
5 Если все элементы бесконечно малой последователь –ности 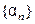 равны одному и тому же числу
равны одному и тому же числу 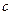 , то
, то 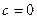
Следующая теорема устанавливает связь между бесконечно малыми и бесконечно большими последовательностями.
ТЕОРЕМА 1 Если  - бесконечно большая последова- тельность то
- бесконечно большая последова- тельность то 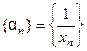 является бесконечно малой, и наоборот, если
является бесконечно малой, и наоборот, если 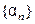 - бесконечно малая последовательность, то последовательность
- бесконечно малая последовательность, то последовательность 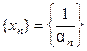
 является бесконечно большой.
является бесконечно большой.
Д о к а з а т е л ь с т в о. Следует отметить, что у бесконечно большой последовательности только конечное число элементов может быть равно нулю Это следует из определения бесконечно большой последовательности, так как существует номер 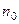 , начиная с которого для всех элементов выполняется неравенство
, начиная с которого для всех элементов выполняется неравенство 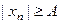 . Это означает, что для всех
. Это означает, что для всех 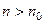 элементы последовательности
элементы последовательности  не равны нулю и поэтому последовательность
не равны нулю и поэтому последовательность 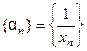 имеет смысл, если её элементы начинать рассматривать начиная с номера
имеет смысл, если её элементы начинать рассматривать начиная с номера 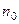 . Докажем, что последовательность
. Докажем, что последовательность 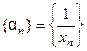 бесконечно малая. Возьмём произвольное число
бесконечно малая. Возьмём произвольное число 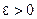 . Для числа
. Для числа 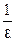 можем указать номер
можем указать номер 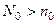 , начиная с которого ве элементы последовательности
, начиная с которого ве элементы последовательности  удовлетворяют неравенству
удовлетворяют неравенству 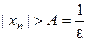 . Тогда, начиная с этого номера, будет выполняться неравенство
. Тогда, начиная с этого номера, будет выполняться неравенство 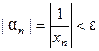 . Таким образом доказано, что последовательность
. Таким образом доказано, что последовательность 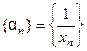 является бесконечно малой. Аналогично доказывается второе утверждение теоремы.
является бесконечно малой. Аналогично доказывается второе утверждение теоремы.
2.3. Предел числовой последовательности. Свойства сходящихся последовательностей.
О п р е д е л е н и е 1 Число 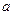 называется пределом число- вой последовательности
называется пределом число- вой последовательности  при
при 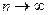 , если для любого числа
, если для любого числа 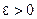 существует номер
существует номер 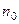 , начиная с которого все элементы последовательности удовлетворяют неравенству
, начиная с которого все элементы последовательности удовлетворяют неравенству
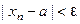 . (3)
. (3)
Символически это записывается так 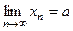 , или
, или 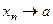 при
при 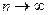 .
.
Если последовательность  имеет предел, то её называют сходящейся; ели же предела не существует, то её называют расходящейся.
имеет предел, то её называют сходящейся; ели же предела не существует, то её называют расходящейся.
Замечание 1 В соответствии с этим определением, всякая бесконечно малая последовательность имеет предел и этот предел равен нулю.
Замечание 2 Бесконечно большие последовательности иногда называют последовательностями, сходящимися к бесконечности и записывают 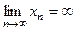 .
.
Замечание 3. Если 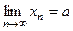 , то последовательность
, то последовательность 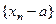 является бесконечно малой. Следовательно, любой элемент сходящейся последовательность можно представить в виде
является бесконечно малой. Следовательно, любой элемент сходящейся последовательность можно представить в виде
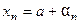 , (4)
, (4)
где 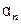 - элемент бесконечно малой последовательности.
- элемент бесконечно малой последовательности.
Замечание 4. Неравенство (3) равносильно неравенствам 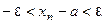 или
или 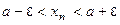 . Последнее неравен -ство означает, что элементы
. Последнее неравен -ство означает, что элементы 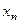 находятся в
находятся в 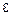 - окрестности точки
- окрестности точки 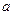 . В соответствии с этим получаем ещё одно опреде -ление сходящейся последовательности:
. В соответствии с этим получаем ещё одно опреде -ление сходящейся последовательности:
О п р е д е л е н и е 2. Последовательность  называется сходящейся, если существует число
называется сходящейся, если существует число 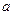 такое, что в любой
такое, что в любой 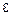 - окрестности этого числа находятся все элементы последова -тельности
- окрестности этого числа находятся все элементы последова -тельности  , начиная с некоторого номера.
, начиная с некоторого номера.
Рассмотрим примеры сходящихся последовательностей.
- Последовательность
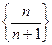 сходится и предел этой последовательности равен 1. В самом деле, разность
сходится и предел этой последовательности равен 1. В самом деле, разность 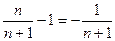 и для доказательства сходимости достаточно убедиться, что последовательность
и для доказательства сходимости достаточно убедиться, что последовательность 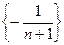 является бесконечно малой. Для произ -вольного
является бесконечно малой. Для произ -вольного 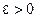 можем взять любой номер
можем взять любой номер 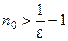 . Тогда
. Тогда 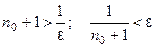 . Следовательно, для всех чисел
. Следовательно, для всех чисел 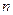 , удовлетворяющих неравенству
, удовлетворяющих неравенству 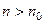 , будет выполнено
, будет выполнено 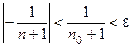 , т.е. последова- тельность
, т.е. последова- тельность 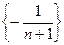 в самом деле бесконечно малая.
в самом деле бесконечно малая. - Последовательность
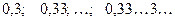 сходится и имеет пределом число
сходится и имеет пределом число 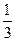 . В самом деле
. В самом деле
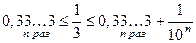 . Из этих неравенств получается
. Из этих неравенств получается 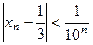 . Так как при
. Так как при 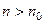 ,
, 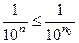 , то для произвольно взятого
, то для произвольно взятого 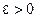 , выбрав номер
, выбрав номер 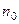 из условия
из условия 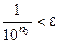 , получим
, получим 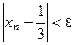 при
при 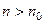 .
.
Основные свойства сходящихся последовательностей:
- Сходящаяся последовательность имеет только один предел.
- Сходящаяся последовательность ограничена.
- Алгебраическая сумма сходящихся последовательностей является сходящейся последовательностью, причём, если
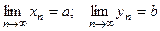 , то
, то 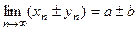 .
. - Произведение сходящихся последовательностей является сходящейся последовательностью, причём, если
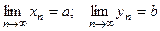 , то
, то 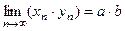 .
.
5. Частное двух сходящихся последовательностей  и
и
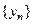 , при условии, что предел
, при условии, что предел 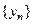 не равен нулю,
не равен нулю,
является сходящейся последовательностью, предел
которой равен частному пределов последовательностей
 и
и 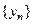
6. Из сходимости последовательности 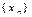 следует
следует
сходимость последовательностей
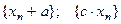 для любых чисел
для любых чисел 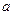 и
и 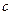 .
.
7. Если все элементы некоторой сходящейся последовательности  , начиная с некоторого номера, удовлетворяют неравенству
, начиная с некоторого номера, удовлетворяют неравенству 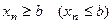 , то и предел этой последовательности -
, то и предел этой последовательности - 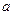 удовлетворяет такому же неравенству, т.е.
удовлетворяет такому же неравенству, т.е. 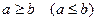 .
.
8. Если элементы сходящихся последовательностей
 и
и 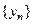 , начиная с некоторого номера, удовлетво-
, начиная с некоторого номера, удовлетво-
ряют неравенству 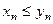 , то их пределы удовлетворя-
, то их пределы удовлетворя-
ют тому же неравенству, т.е. 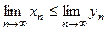 .
.
9. Если все элементы сходящейся последовательности  находятся в отрезке
находятся в отрезке  , то её предел также находится в этом отрезке.
, то её предел также находится в этом отрезке.
10. Пусть  и
и 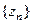 - сходящиеся последовательности, причём
- сходящиеся последовательности, причём 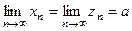 . Пусть, кроме этого, начи- ная с некоторого номера, элементы последовательнос- ти
. Пусть, кроме этого, начи- ная с некоторого номера, элементы последовательнос- ти 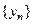 удовлетворяют неравенству:
удовлетворяют неравенству: 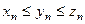 . Тогда последовательность
. Тогда последовательность 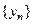 также сходится и имеет предел, равный
также сходится и имеет предел, равный 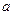 .
.
Замечание В соответствии с теоремой 1 из 1.3, любая
последовательность вида 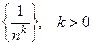 , является бесконечно малой, т.е.
, является бесконечно малой, т.е. 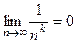 . Поэтому, учитывая свойства 3 – 7 сходящихся последовательностей, можем легко вычислять следующие пределы:
. Поэтому, учитывая свойства 3 – 7 сходящихся последовательностей, можем легко вычислять следующие пределы:
Пример 1. Найти предел 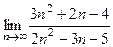 . Разделим чис- тель и знаменатель дроби на
. Разделим чис- тель и знаменатель дроби на 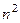 . В результате получим
. В результате получим 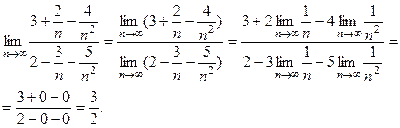
В дальнейшем, при вычислении пределов такого вида, ни к чему повторять такую последовательность операций. Легко проверить и следует запомнить следующее правило:
ПРАВИЛО: Если в дроби старшая степень числителя меньше старшей степени знаменателя, то предел равен нулю; если старшая степень числителя больше старшей степени знаменателя, то предел равен бесконечности; если старшие степени числителя и знаменателя совпадают, то предел равен отношению коэффициентов перед старшими степенями.
Рассмотрим ещё один пример:
Пример 2. Вычислить предел
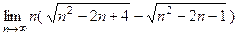 .
.
Под знаком предела находится неопределённое выражение вида 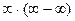 . Для вычисления такого предела желательно сначала получить дробь и затем использовать правило. Для этого умножим и разделим это выражение на сумму корней, чтобы получить в числителе разность квадратов. Получим:
. Для вычисления такого предела желательно сначала получить дробь и затем использовать правило. Для этого умножим и разделим это выражение на сумму корней, чтобы получить в числителе разность квадратов. Получим:
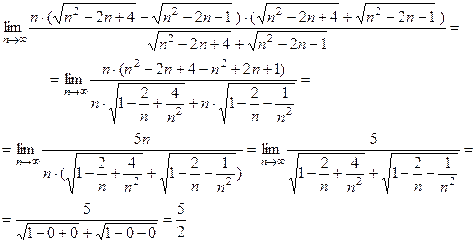
2.4. Монотонные последовательности.
О п р е д е л е н и е Последовательность  называется убы- вающей, если для всех
называется убы- вающей, если для всех 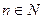 выполняется неравенство
выполняется неравенство 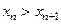 ; последовательность
; последовательность  называется невозраста -ющей, если для всех
называется невозраста -ющей, если для всех 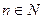 выполняется неравенство
выполняется неравенство 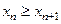 ; последовательность
; последовательность  называется возрастаю -щей, если для всех
называется возрастаю -щей, если для всех 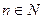 выполняется неравенство
выполняется неравенство 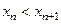 ; последовательность
; последовательность  называется неубываю -щей, если для всех
называется неубываю -щей, если для всех 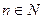 выполняется неравенство
выполняется неравенство 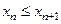 . Во всех этих случаях последовательность называется монотонной.
. Во всех этих случаях последовательность называется монотонной.
Например, 1. Последовательность 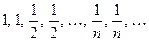 является невозрастающей. Она ограничена сверху своим первым элементом 1, а снизу числом 0.
является невозрастающей. Она ограничена сверху своим первым элементом 1, а снизу числом 0.
2. Последовательность 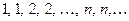 является неубывающей. Она ограничена снизу числом 1, а сверху неограниченна.
является неубывающей. Она ограничена снизу числом 1, а сверху неограниченна.
3. Последовательность 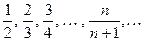 является возрастающей и ограниченной с двух сторон - снизу числом 0, сверху - числом 1.
является возрастающей и ограниченной с двух сторон - снизу числом 0, сверху - числом 1.
Признак сходимости монотонной последовательности Если неубывающая (невозрастающая) последовательность  ограничена сверху (снизу), то она сходится, или, иначе, этот признак можно сформулировать так: если монотонная последовательность ограничена с обоих сторон, то она сходится.
ограничена сверху (снизу), то она сходится, или, иначе, этот признак можно сформулировать так: если монотонная последовательность ограничена с обоих сторон, то она сходится.
Замечание: условие ограниченности монотонной последова -тельности является необходимым и достаточным условием сходимости.
Следствием этого признака является так называемая
ТЕОРЕМА (О вложенных отрезках) Пусть дана бесконечная система отрезков 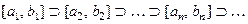 и пусть длины этих отрезков:
и пусть длины этих отрезков: 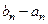 стремятся к нулю при
стремятся к нулю при 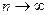 . Тогда существует, и притом единственная, точка
. Тогда существует, и притом единственная, точка 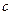 , принадлежащая всем отрезкам этой системы.
, принадлежащая всем отрезкам этой системы.
Доказательство. Прежде всего следует заметить, что точка 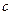 , общая для всех отрезков, может быть только одна. В самом деле, если бы нашлась ещё одна точка
, общая для всех отрезков, может быть только одна. В самом деле, если бы нашлась ещё одна точка 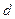 , принадлежащая всем отрезкам, то и весь отрезок
, принадлежащая всем отрезкам, то и весь отрезок 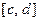 принадлежал бы всем отрезкам
принадлежал бы всем отрезкам 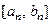 . Тогда для всех
. Тогда для всех 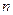 выполнялось бы неравенство
выполнялось бы неравенство 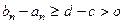 . Но это невозможно, так как
. Но это невозможно, так как 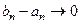 при
при 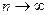 . Докажем теперь существование точки
. Докажем теперь существование точки 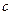 . Так как последовательность отрезков является стягивающейся, то последовательность левых концов
. Так как последовательность отрезков является стягивающейся, то последовательность левых концов 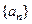 является неубывающей, а последова –тельность правых концов
является неубывающей, а последова –тельность правых концов 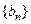 - невозрастающей. Поскольку обе эти последовательности ограничены (все элементы этих
- невозрастающей. Поскольку обе эти последовательности ограничены (все элементы этих
последовательностей содержатся в отрезке 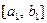 ), то по признаку сходимости они обе сходятся. Но из того, что последовательность
), то по признаку сходимости они обе сходятся. Но из того, что последовательность 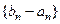 является бесконечно малой, следует, что обе последовательности имеют тот же предел, который мы можем обозначить
является бесконечно малой, следует, что обе последовательности имеют тот же предел, который мы можем обозначить 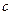 , причём для всех
, причём для всех 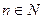 выполняется неравенство
выполняется неравенство  , т.е. точка
, т.е. точка 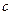 - общая для всех отрезков.
- общая для всех отрезков.
Ещё одним следствием признака сходимости монотонных последовательностей является доказательство существования предела последовательности 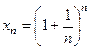 , которая ограничена снизу числом 2, а сверху - числом 3. Предел этой последовательности считаем, по определению равным
, которая ограничена снизу числом 2, а сверху - числом 3. Предел этой последовательности считаем, по определению равным 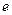 , т.е.
, т.е.
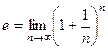 .
.
