Графы. основные понятия и алгоритмы

Почему теория графов так важна для программиста?

Во-первых, графы могут рассматриваться как модели самих программ, данных и процессов. Э. Дейкстра высказал однажды такую мысль: при грамотном программировании на тысячу строк программного текста нужно написать в десять раз больше рассуждений и доказательств, гарантирующих применимость программы.

Во-вторых, графы служат удобной структурой данных для представления объектов обработки информации. Расширение традиционного круга задач, решаемых на ЭВМ (перевод текста, распознавание речи, составление расписаний, игровые программы, экспертные и информационные системы и т.д.), за последние несколько десятков лет превратили комбинаторику и теорию графов в основной инструмент решения огромного числа задач.

Рассмотрим основные методы конструирования алгоритмов на графах, в особенности, методы систематического обхода графа. Также будут рассмотрены несколько задач, являющихся модельными для большого класса задач.

Для них будут даны: алгоритм решения + анализ его вычислительной сложности. Алгоритмы представляют собой сжатые варианты программ, написанных на паскалеподобном языке.

Вычислительная сложность равна числу элементарных шагов, выполняемых алгоритмом в самом плохом случае, и зависит от размерности входных данных.

Объясним более точно, что подразумевается под «элементарным шагом».

Допустим, что транслятор типичной ЭВМ переводит программу в машинный язык, имеющий арифметические операции, условные переходы, операции ввода-вывода, команды переноса из памяти в буфер и т.д. Выполнение любой такой операции будем считать элементарным шагом.

Очевидно, что сложность алгоритма будет зависеть от конкретного транслятора. Однако нас будет интересовать не абсолютная сложность, а с точностью до умножения на произвольную постоянную. Другими словами, нас интересует, как быстро растет сложность при неограниченном увеличении размерности входных данных. Такая сложность называется асимптотической и не зависит от способа трансляции.

Будем использовать следующие обозначения.

Пусть f(n) и g(n) – неотрицательные функции, n – размерность задачи, C>0 – некоторая постоянная. Тогда f(n) имеет порядок О(g(n)), если f(n)£ C*g(n) для всех n, больших некоторого номера. Читается это так: «f(n) порядка не более, чем g(n)». Определенная таким образом сложность иногда называется временной, в отличие от сложности по памяти.

Напомним читателю лишь основные определения теории графов. Желающих ознакомиться с графами более подробно отошлем к книге О. Оре «Графы и их применение» или к любом учебнику по дискретной математике. Итак, нанесем на плоскость несколько точек и некоторые из них соединим попарно (рис. 8.1).

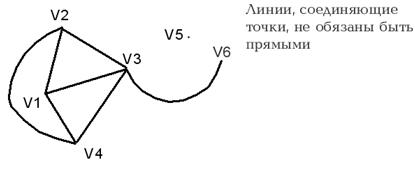
Рис. 8.1. Граф

У нас получился граф. Точки изображают вершины, а соединяющие их линии соответствуют ребрам. Дадим имена вершинам и запишем математическое определение графа.

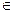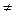Неориентированным графомбудем называть такую произвольную пару G=<V, E>, что E {(u–v): u, v V и u v}.

V – множество вершин, Е – множество ребер графа G. Наш рисунок – это изображение графа на плоскости.

Если граф на плоскости можно изобразить так, чтобы его ребра пересекались только в вершинах, он называется планарным или плоским.

Если ребро е графа G соединяет две вершины u и v, то будем говорить, что u и v смежны между собой.

Степень вершины определим как число ребер, смежных ей.

Вершину нулевой степени будем называть изолированной (V₅ на рис. 8.1).

Вопрос 1. Чему равна степень вершины V₃ на рис. 8.1?

Путем в графе G=<V, E> назовем последовательность вершин V₁, V₂, …, V_k такую, что k 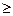0 и любые две соседние вершины соединены ребром. Для неориентированных графов вместо термина «путь» часто используют термин «цепь». Вершины V₀ и V_k будем называть началом и концом пути, k – длиной пути.

Путь, начало и конец которого совпадают, назовем циклом.

Если все ребра пути (цикла) различны, будем говорить о простом пути (цикле).

Если все вершины V₁, …, V_k различны, будем говорить об элементарном пути.

Если вершины цикла, кроме V₁=V_k, различны, получим элементарный цикл.

Вопрос 2. Перечислите все элементарные циклы графа G на рис. 8.1.

Подграфом G' графа G будем называть такой произвольный граф G'=<V', E'>, что V'V и E' E.

Если для любой пары вершин существует путь, их соединяющий, то граф связный.

У несвязного графа не все вершины можно соединить путем с фиксированной вершиной x. Те вершины, которые можно соединить путем с x, и смежные им ребра образуют связную компонентувершины x. Граф на рис. 8.1 двусвязен.

Вопрос 3. Перечислите элементы, входящие в компоненты связности графа G (см. рис. 8.1).

Деревом называется связный граф, не содержащий циклов (рис. 8.2).

Рис. 8.2. Дерево

Вопрос 4. Сколько ребер у дерева с 9 вершинами?

Ответ 1. 4.

Ответ 2.(V₂-V₄-V₃-V₂), (V₂-V₁-V₄-V₃-V₂), (V₂-V₁-V₃-V₂), (V₄-V₃-V₁-V₄), (V₂-V₄-V₁-V₃-V₂), (V₂-V₄-V₁-V₂), (V₁-V₂-V₄-V₃-V₁).

Ответ 3. 1-я компонента – вершины {V₁, V₂, V₃, V₄, V₆} и соединяющие их ребра. 2-я компонента – {V₅}.

Ответ 4. Дерево с двумя вершинами имеет одно ребро. Всякий раз, присоединяя к дереву следующую вершину, присоединяем одно ребро. Для дерева m = n -1. Для n = 9: m = 8.