Линейные многошаговые методы

Пусть требуется найти решение 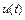на отрезке 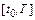задачи Коши

.

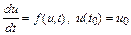Предположим, что построены приближенные значения решения 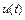и его первой производной 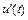в моменты времени 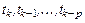, т. е.

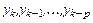
и

.

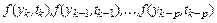Общий вид разностной схемы рассматриваемых здесь многошаговых методов имеет вид

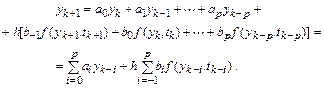
где 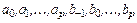– коэффициенты (их всего 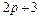), которые должны быть определены при получении конкретного многошагового метода, 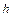– шаг интегрирования.

Значения этих 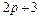коэффициентов выбирают так, что если решение 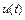является полиномом степени 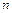, то разностная схема многошагового метода дает точное значение, т. е. 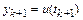. Поскольку полином степени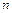

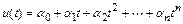
имеет 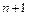параметр, то разностная схема должна иметь по крайней мере 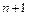коэффициент. В большинстве практических многошаговых методов 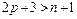и лишние коэффициенты могут быть выбраны произвольно.

Получим соотношения, которым должны удовлетворять все 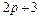коэффициента разностной схемы в предположении, что метод дает точное решение для задачи Коши, точным решением которой является полином степени 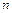. Поскольку полином 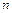-й степени включает в себя все полиномы степени ниже 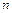, то разностная схема должна также давать точное решение для всех задач Коши, имеющих полиномиальное решение степени меньшей, чем 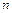. В частности:

1. 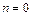, 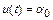. Класс задач с таким решением задается уравнением

.

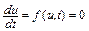Поэтому 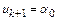, , 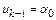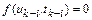. Подставив эти значения в разностную схему, получим первое условие, которому должны удовлетворять коэффициенты :

.

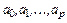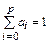2. 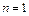, 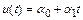. Класс задач с таким решением задается в виде

.

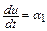Для удобства выберем 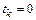. Тогда 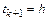, , 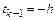, 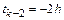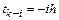. В этом случае

.

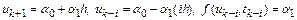Подставим их в разностную схему:

.

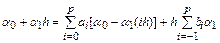Если учесть первое условие, то это соотношение преобразуется к виду

.

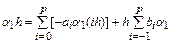Наконец, разделив левую и правую части на 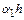, получим условие корректности для полиномиальных решений первой степени:

.

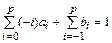3. 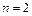, 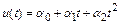. Класс задач с таким решением

.

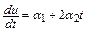Полагаем, как и прежде, 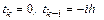и находим, что

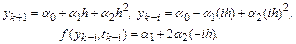
Перепишем с учетом этих соотношений разностную схему многошагового метода

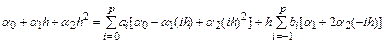
или

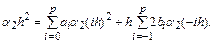
Разделим левую и правую части этого соотношения на 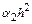. Условие корректности для полиномиальных решений второй степени примет следующий вид:

.

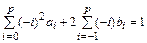4. Общий случай: 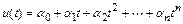. Класс задач с таким решением

.

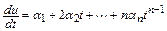Условие корректности для полиномиальных решений степени :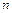

.

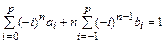Анализ выписанных условий корректности для полиномиальных решений до степени 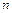включительно свидетельствует, что они имеют одинаковую форму, а именно:

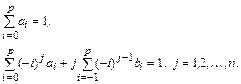
Этим соотношениям должны удовлетворять все 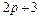коэффициента разностной схемы линейного многошагового метода.

Лекция 12

Многошаговые методы

ЦЕЛЬ ЛЕКЦИИ: На основе общей разностной схемы линейных многошаговых методов и условий корректного выбора коэффициентов построить явные многошаговые методы Адамса, неявные многошаговые методы Адамса, неявные многошаговые методы Гира различных порядков точности.