Математические методы описания дискретных систем

Дискретные системы автоматического управления.

Основные положения.

К дискретным системам относятся импульсные системы регулирования и системы, включающие в себя цифровую вычислительную машину (ЦВМ).

Импульсная система регулирования отличается от непрерывной наличием в канале управления импульсного элемента, преобразующего непрерывную величину в последовательность импульсов той или иной формы.

f(t)

W(S)

e(t) ИЭ e^*(t)

Ä

g(t) T x(t)

На рисунке импульсный элемент ИЭ установлен в канале управления, который является каналом ошибки. Последовательность импульсов с периодом Т поступает на непрерывную часть системы с передаточной функцией W(S). Как и ранее g(t) - входное воздействие, x(t)- регулируемая величина, ε(t)- ошибка САР, f(t)- возмущение.

Форма импульсов, генерируемых импульсным элементом, вообще говоря, оказывает влияние на динамику системы регулирования. Однако, в том случае, когда длительность импульсов мала по сравнению со временем переходного процесса непрерывной части, можно пренебречь влиянием, как формы импульса, так и принципа модуляции (амплитудная или широтная).

В этом случае последовательность реальных импульсов может быть заменена последовательностью δ-функций, модулируемых по площади. Реакция непрерывной части на каждый такой импульс представляет в этом случае ее весовую функцию (импульсную переходную характеристику), умноженную на коэффициент, равный площади импульса.

Огромные вычислительные и логические возможности ЭВМ определяют большие перспективы их использования при управлении объектами. Они вводятся в систему регулирования, когда требуется обрабатывать большие объемы информации и когда на ЭВМ возлагается решение ряда задач с обслуживанием нескольких зависимых или независимых каналов управления.

В наиболее схематическом виде система регулирования с ЭВМ изображена на рисунке.

Здесь g₁, g₂,…g_n-входные воздействия.

x_1, x_2, x₃…x_n-регулируемые величины.

u_1, u_2, u₃…u_n- выходные управляющие воздействия.

f_1, f_2, f₃…f_n- возмущения.

Рассмотрение системы со многими регулируемыми величинами представляет собой весьма громоздкую задачу. В дальнейшем ограничимся рассмотрением случая, когда ЭВМ вводится в одиночный контур с одной регулируемой величиной х и одним входным воздействием g, к которому могут быть сведены многие практические задачи.

АЦП γ ε₁ ЦАП ε₂ ε₃ ε₄

АПЦ

Здесь: АЦП- преобразователь аналог-код;

ЦАП- преобразователь код-аналог;

Т- период дискретности ЭВМ;

W_о(s) - передаточная функция объекта;

D(z)- алгоритм работы ЭВМ;

τ- временное запаздывание, вносимое ЭВМ;

W_э(s)- передаточная функция экстраполятора.

Обычно экстраполирующее устройство представляет собой фиксатор, удерживающий выходной сигнал ЭВМ на одном уровне в течение такта работы машины. Этот случай, так называемого экстраполятора нулевого порядка, является наиболее распространенным. В более сложных случаях экстраполятор может внутри такта работы машины изменять выходной сигнал по линейному закону (экстраполятор первого порядка), по закону квадратичной параболы (экстраполятор второго порядка) и т.д.

Нелинейность, вносимая входными и выходными преобразователями, может быть представлена в виде нелинейных статических характеристик релейного типа. Они представляют собой многоступенчатую релейную характеристику. Число уровней характеристики m связано с числом двоичных разрядов n зависимостью.

m=2ⁿ-1

Во входных преобразователях число разрядов обычно велико (10 - 20). Поэтому влиянием нелинейности АЦП часто можно пренебречь.

Во входных (ЦАП) преобразователях число разрядов бывает обычно малым, достигая в пределе одного. Это объясняется тем, что выходной преобразователь установлен, по существу, в канале ошибки САР, поэтому нелинейность выходного преобразователя может оказывать влияние на динамику замкнутой САР с ЭВМ. И это надо учитывать.

Во многих случаях представляется возможным пренебречь влиянием нелинейностью выходных преобразователей. Это позволяет свести САР с ЭВМ к линейной импульсной системе и воспользоваться хорошо развитым аппаратом расчета таких систем.

В простейшем случае, когда на ЭВМ возлагается задача определения ошибки 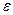=g-x необходимо положить на структурной схеме D(z)=1. При использовании т.н. дискретной коррекции на ЭВМ возлагается задача улучшения динамических характеристик САР. В этом случае D(z)¹1.

На схеме наиболее простой способ использования ЭВМ в САР. Возможны более сложные случаи комбинированного управления, когда ЭВМ формирует выходной сигнал в функции не только ошибки 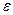=g-x но и вводит дополнительно сигнал пропорциональный скорости и ускорению изменения входного воздействия g^/(t) и g^//(t). Могут встречаться и иные схемы.

Математические методы описания дискретных систем

Решетчатые функции

Наряду с функциями, определенными на всей вещественной прямой t, можно рассматривать функции, которые определены только в некоторых точках t₁,t₂… Такие функции называют решетчатыми. Мы будем рассматривать функции, определенные только в равноотстоящих точках t=nT, где n- любое целое число, а T- постоянная, называемая периодом дискретности. Эти функции принято обозначать f[nT].

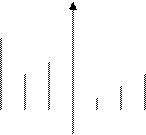f[ nT]

-3Т -2Т -Т 0 Т 2Т 3Т

Любой непрерывной функции f(t) можно поставить в соответствие некоторое множество решетчатых функций, если представить переменную t в виде

t=nT+eT (0£e£1)

При каждом фиксированном значении переменной e функцию f(nT+eT) можно рассматривать как решетчатую функцию, определенную в точках eT, (e+1)T, (e+2)T,… Такие функции называются смещенными решетчатыми функциями. Для них принято обозначение f(nT+eT)=f[nT, eT]. Изменяя e в пределах от 0 до 1, можно получить множество смещенных решетчатых функций f[nT, eT], соответствующих данной непрерывной функции f(t).

f[t]

f[nT,0]

-T 0 T 2T 3T

f[nT,ε₁T]

ε₁T

f[nT,ε₂T]

ε₂T

Благодаря непрерывности функции f(t), функция f[nT, eT] является непрерывной по аргументу e и удовлетворяет условию:

f[(n-1)T, T]=f[nT, 0]

Если функция f(t) терпит разрыв непрерывности первого рода в точках t=nT, то написанное равенство не выполняется поскольку

lim f[(n-1)T, eT] ¹ lim [nT, eT]

e®1 e®0

В этом случае под значением функции будем понимать предел справа.

f[nT] = lim f[nT, eT]

e®0