IV Сравнение всех полученных решений. Анализ с экономической точки зрения, выводы
При решении задач различными методами получился один ответ, это означает, что задача решена верно.
Т.е. для получения максимального дохода торгового предприятия равной 55.09 руб., необходимо реализовать товара группы А 8.18 ед., группы В – 7.45.
Площадь торговых помещений и накладные расходы используются полностью (24 и 32), а рабочее время продавцов и площадь складских помещений недоиспользуется (0.2 и соответственно 4.3).
V Электронные варианты решений.
| Microsoft Excel 11.0 Отчет по пределам | |||||||||
| Целевое | |||||||||
| Ячейка | Имя | Значение | |||||||
| $D$6 | коэф ЦФ ЗНАЧЕНИЕ | 55,09 | |||||||
| Изменяемое | Нижний | Целевой | Верхний | Целевой | |||||
| Ячейка | Имя | Значение | предел | результат | предел | результат | |||
| $B$3 | значение Х1 | 8,18 | 22,36 | 8,18 | 55,09 | ||||
| $C$3 | значение Х2 | 7,45 | 32,73 | 7,45 | 55,09 |
| Microsoft Excel 11.0 Отчет по устойчивости | |||||||
| Изменяемые ячейки | |||||||
| Результ. | Нормир. | Целевой | Допустимое | Допустимое | |||
| Ячейка | Имя | значение | стоимость | Коэффициент | Увеличение | Уменьшение | |
| $B$3 | значение Х1 | 8,18 | 3,8 | ||||
| $C$3 | значение Х2 | 7,45 | 1,67 | ||||
| Ограничения | |||||||
| Результ. | Теневая | Ограничение | Допустимое | Допустимое | |||
| Ячейка | Имя | значение | Цена | Правая часть | Увеличение | Уменьшение | |
| $D$12 | огран 3 лев часть | 1,29 | 0,97 | ||||
| $D$10 | огран 1 лев часть | 0,57 | 7,2 | ||||
| $D$11 | огран 2 лев часть | 4,84 | 1E+30 | 0,16 |
| Microsoft Excel 11.0 Отчет по результатам | ||||||
| Целевая ячейка (Максимум) | ||||||
| Ячейка | Имя | Исходное значение | Результат | |||
| $D$6 | коэф ЦФ ЗНАЧЕНИЕ | 55,09090909 | ||||
| Изменяемые ячейки | ||||||
| Ячейка | Имя | Исходное значение | Результат | |||
| $B$3 | значение Х1 | 8,181818182 | ||||
| $C$3 | значение Х2 | 7,454545455 | ||||
| Ограничения | ||||||
| Ячейка | Имя | Значение | Формула | Статус | Разница | |
| $D$12 | огран 3 лев часть | $D$12<=$F$12 | связанное | |||
| $D$10 | огран 1 лев часть | $D$10<=$F$10 | связанное | |||
| $D$11 | огран 2 лев часть | 4,84 | $D$11<=$F$11 | не связан. | 0,16 | |
| $B$3 | значение Х1 | 8,18 | $B$3>=$B$4 | не связан. | 8,18 | |
| $C$3 | значение Х2 | 7,45 | $C$3>=$C$4 | не связан. | 7,45 |
Задача 2. Транспортная задача.С четырех карьеров, имеющих запасы гравия, соответственно 620, 700, 250, 120 тонн, требуется отвезти его в количестве, соответственно 620, 500, 700 тонн на три стройплощадки.
Расстояние от каждого карьера до каждой стройплощадки представлены в таблице 2.1.
Таблица 2.1 Расстояние от каждого карьера до каждой стройплощадки, км.
| Карьеры | Стройплощадки | ||
Составить оптимальный маршрут перевозок гравия от карьеров на стройплощадки, обеспечивающий минимальные транспортные затраты.
1. Решение задачи методом «северо-западного угла»:
1) Проверка задачи на разрешимость.
Предварительным шагом является проверка того, закрытого или открытого типа задача, то есть проверка выполнения равенства общих запасов поставщиков общим потребностям потребителей, то есть åАi=åBj.
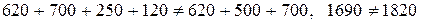 .
.
Делаем вывод, что задача открытого типа. Ее нужно преобразовать в задачу закрытого типа. Для этого вводим фиктивного поставщика, то есть дополнительную строку. В данной строке тарифы клеток фиктивного поставщика будем принимать за ноль. Далее можно решать задачу методом потенциалов.
Построение матрицы задачи.
После проверки задачи на разрешимость, все условия задачи запишем в виде матрицы (таблица 2.2).
Таблица 2.2 Матрица задачи
| Карьеры | Стройплощадки | Сумма запасов | ||
| 5 | 9 | 4 | ||
| 3 | 2 | 2 | ||
| 4 | 6 | 5 | ||
| 2 | 5 | 3 | ||
| 0 | 0 | 0 | ||
| Сумма потребностей |
3) Решение задачи методом потенциалов.
На основе матрицы задачи построим первый исходный план перевозок и запишем результаты в транспортную схему 1 (таблица 2.3).
Таблица 2.3 Транспортная схема 1
| Карьеры | Стройплощадки | Сумма запасов | ||
| 620 5 | 9 | 4 | ||
| 3 | 500 2 | 200 2 | ||
| 4 | 6 | 250 5 | ||
| 2 | 5 | 120 3 | ||
| 0 | 0 | 130 0 | ||
| Сумма потребностей |
Итерация 1
Шаг1
Выписываем исходное допустимое базисное решение, то есть первый план перевозок и вычисляем соответствующее ему значение целевой функции.
 620 0 0
620 0 0
0 500 200
Х1 = 0 0 250
0 0 120
0 0 130
Z1 = 5*620 + 2*250 + 2*200 + 5*250 + 3*120=6110
Проверим план на вырожденность, то есть проверим условие: количество занятых клеток должно быть равно величине m+n-1. Таким образом, 5 + 3 – 1 =7. Вывод: план вырожденный. Для того, чтобы план стал невырожденным, добавим в ячейку С1,2 нулевую поставку и будем считать эту клетку занятой.
Шаг 2.
Проверяем план на оптимальность.
Таблица 2.4 Транспортная схема 2
| Карьеры | Стройплощадки | Сумма запасов | Ui | ||
| 620 5 |   0 9 0 9 |  Х+ 4 Х+ 4 | |||
| 3 |  500 2 500 2 | 200 2 | -7 | ||
| 4 | 6 | 250 5 | -4 | ||
| 2 | 5 | 120 3 | -6 | ||
| 0 | 0 | 130 0 | -9 | ||
| Сумма потребностей | |||||
| Vj |
С1,3 = 4³0+9 (-) С2,1 = 3³-7+5 (+) С3,1 = 4³-4+5 (+)
С3,2 = 6³-4+9 (+) С4,1= 2³-6+5 (+) С4,2 = 5³-6+9 (+)
С5,1 = 0³-9+5 (+) С5,2 = 0³-9+9 (+)
Вывод: так как не для всех пустых клеток выполняется соотношение
Cij ³ Ui + Vj (*), то план представленный в транспортной схеме 1 не оптимальный, его нужно улучшить.
Шаг 3.
Выполнение процесса улучшение плана. Для этого определим, из какого карьера и на какую стройплощадку произведется перепоставка, и ее величину (то есть определим какая из прежних базисных неизвестных должна быть выведена из базиса). Клетки в которых не выполняется соотношение (*) – плохие, из всех них выбираем только одну, в данном случае это клетка С1,3.
Процесс улучшения плана выполняем в соответствии с правилом замкнутого маршрута, по которому происходит перераспределение поставок и улучшение ранее построенного плана: маршрут замкнут, то есть начинается с «плохой» клетки и в ней же заканчивается.
Шаг 4.
Строим новый план с намеченными на шаге 3 изменениями и занесем результаты в транспортную схему 3 ( таблица 2.5).
Таблица 2.5 Транспортная схема 3
| Карьеры | Стройплощадки | Сумма запасов | Ui | ||
  620 5 620 5 | 9 |  0 4 0 4 | |||
| 3 | 500 2 | 200 2 | -2 | ||
 Х+ 4 Х+ 4 | 6 | 250 5 | |||
| 2 | 5 | 120 3 | -1 | ||
| 0 | 0 | 130 0 | -4 | ||
| Сумма потребностей | |||||
| Vj |
Итерация 2
Шаг 1
Выписываем исходное допустимое базисное решение, то есть первый план перевозок и вычисляем соответствующее ему значение целевой функции.
 620 0 0
620 0 0
0 500 200
Х2 = 0 0 250
0 0 120
0 0 130
Z2 = 5*620 + 2*250 + 2*200 + 5*250 + 3*120=6110
Шаг 2.
Проверяем план на оптимальность.
С1,2 = 9³0+2 (+) С2,1 = 3³-2+5 (+) С3,1 = 4³1+5 (-)
С3,2 = 6³1+2 (+) С4,1= 2³-1+5 (-) С4,2 = 5³-1+2 (+)
С5,1 = 0³-4+5 (+) С5,2 = 0³-4+2 (+)
Вывод: так как не для всех пустых клеток выполняется соотношение
Cij ³ Ui + Vj (*), то план представленный в транспортной схеме 3 не оптимальный, его нужно улучшить.
Шаг 3
Выполнение процесса улучшение плана.
Для этого определим из какого карьера, на какую стройплощадку произведется перепоставка и ее величину (то есть определим какая из прежних базисных неизвестных должна быть выведена из базиса). Клетки в которых не выполняется соотношение (*) – плохие, из всех них выбираем только одну, в данном случае это клетка С3,1.
Процесс улучшения плана выполняем в соответствии с правилом замкнутого маршрута, по которому происходит перераспределение поставок и улучшение ранее построенного плана: маршрут замкнут, то есть начинается с плохой клетки и в ней же заканчивается.
Шаг 4.
Строим новый план с намеченными на шаге 3 изменениями и занесем результаты в транспортную схему 4 (таблица 2.6).
Таблица 2.6 Транспортная схема 4
| Карьеры | Стройплощадки | Сумма запасов | Ui | ||
  370 5 370 5 | 9 |  250 4 250 4 | |||
| 3 | 500 2 | 200 2 | -2 | ||
| 250 4 | 6 | 5 | -1 | ||
 Х+ 2 Х+ 2 | 5 | 120 3 | -1 | ||
| 0 | 0 | 130 0 | -4 | ||
| Сумма потребностей | |||||
| Vj |
Итерация 3
Шаг 1
Выписываем исходное допустимое базисное решение, то есть первый план перевозок и вычисляем соответствующее ему значение целевой функции.
 370 0 250
370 0 250
0 500 200
Х3 = 250 0 0
0 0 120
0 0 130
Z3 = 5*370 + 4*250 + 2*500 + 2*200 + 4*250 + 3*120=5610
Шаг 2.
Проверяем план на оптимальность.
С1,2 = 9³0+2 (+) С2,1 = 3³-2+5 (+) С3,2 = 6³-1+2 (+)
С3,3 = 5³-1+4 (+) С4,1= 2³-1+5 (-) С4,2 = 5³-1+2 (+)
С5,1 = 0³-4+5 (+) С5,2 = 0³-4+2 (+)
Вывод: так как не для всех пустых клеток выполняется соотношение
Cij ³ Ui + Vj (*), то план представленный в транспортной схеме 4 не оптимальный, его нужно улучшить.
Шаг 3
Выполнение процесса улучшение плана.
Для этого определим из какого карьера, на какую стройплощадку произведется перепоставка и ее величину (то есть определим какая из прежних базисных неизвестных должна быть выведена из базиса). Клетки в которых не выполняется соотношение (*) – плохие, из всех них выбираем только одну, в данном случае это клетка С4,1.
Процесс улучшения плана выполняем в соответствии с правилом замкнутого маршрута, по которому происходит перераспределение поставок и улучшение ранее построенного плана: маршрут замкнут, то есть начинается с плохой клетки и в ней же заканчивается.
Шаг 4.
Строим новый план с намеченными на шаге 3 изменениями и занесем результаты в транспортную схему 5 (таблица 2.7).
Таблица 2.7 Транспортная схема 5
| Карьеры | Стройплощадки | Сумма запасов | Ui | ||
  250 5 250 5 | 9 |  370 4 370 4 | |||
| 3 | 500 2 | 200 2 | -2 | ||
| 250 4 | 6 | 5 | -1 | ||
| 120 2 | 5 | 3 | -3 | ||
 Х+ 0 Х+ 0 | 0 | 130 0 | -4 | ||
| Сумма потребностей | |||||
| Vj |
Итерация 4
Шаг 1
Выписываем исходное допустимое базисное решение, то есть первый план перевозок и вычисляем соответствующее ему значение целевой функции.
 250 0 370
250 0 370
0 500 200
Х4 = 250 0 0
120 0 0
0 0 130
Z4 = 5*250 + 4*370 + 2*500 + 2*200 + 4*250 + 2*120=5370
Шаг 2.
Проверяем план на оптимальность.
С1,2 = 9³0+4 (+) С2,3 = 3³-2+5 (+) С3,2 = 6³-1+4 (+)
С3,3 = 5³-1+4 (+) С4,2= 5³-3+4 (+) С4,3 = 3³-3+4 (+)
С5,1 = 0³-4+5 (-) С5,2 = 0³-4+4 (+)
Вывод: так как не для всех пустых клеток выполняется соотношение
Cij ³ Ui + Vj (*), то план представленный в транспортной схеме 5 не оптимальный, его нужно улучшить.
Шаг 3
Выполнение процесса улучшение плана.
Для этого определим из какого карьера, на какую стройплощадку произведется перепоставка и ее величину (то есть определим какая из прежних базисных неизвестных должна быть выведена из базиса). Клетки в которых не выполняется соотношение (*) – плохие, из всех них выбираем только одну, в данном случае это клетка С5,1.
Процесс улучшения плана выполняем в соответствии с правилом замкнутого маршрута, по которому происходит перераспределение поставок и улучшение ранее построенного плана: маршрут замкнут, то есть начинается с плохой клетки и в ней же заканчивается.
Шаг 4.
Строим новый план с намеченными на шаге 3 изменениями и занесем результаты в транспортную схему 6 (таблица 2.8).
Таблица 2.8 Транспортная схема 6
| Карьеры | Стройплощадки | Сумма запасов | Ui | ||
| 120 5 | 9 | 500 4 | |||
| 3 | 500 2 | 200 2 | -2 | ||
| 250 4 | 6 | 5 | -1 | ||
| 120 2 | 5 | 3 | -3 | ||
| 130 0 | 0 | 0 | -5 | ||
| Сумма потребностей | |||||
| Vj |
Итерация 5
Шаг 1
Выписываем исходное допустимое базисное решение, то есть первый план перевозок и вычисляем соответствующее ему значение целевой функции.
 120 0 500
120 0 500
0 500 200
Х4 = 250 0 0
120 0 0
130 0 0
Z4 = 5*120 + 4*500 + 2*500 + 2*200 + 4*250 + 2*120=5240
Шаг 2.
Проверяем план на оптимальность.
С1,2 = 9³0+4 (+) С2,1 = 3³-2+5 (+) С3,2 = 6³-1+4 (+)
С3,3 = 5³-1+4 (+) С4,2= 5³-3+4 (+) С4,3 = 3³-3+4 (+)
С5,2 = 0³-5+4 (+) С5,3 = 0³-5+4 (+)
Вывод: так как для всех пустых клеток выполняется соотношение
Cij ³ Ui + Vj (*), то план представленный в транспортной схеме 6 оптимальный.
Анализ решения задачи:
Z= 5240
 120 0 500
120 0 500
0 500 200
Х = 250 0 0
120 0 0
130 0 0
Следовательно, оптимальный план перевозок следующий:
С первого карьера на первую стройплощадку гравия необходимо отвезти 120 тонн, на третью – 500 тонн; со второго карьера на вторую стройплощадку необходимо отвезти гравия 500 тонн, на третью – 200 тонн; с третьего карьера на первую стройплощадку – 250 тонн гравия; с четвертого карьера на первую стройплощадку – 120 тонн гравия и с пятого карьера на первую стройплощадку – 130 тонн. Весь гравий вывезен. При этом минимальные грузоперевозки составляют 5240 т/км.
Задача 3
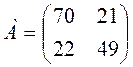
5.1.Решим игру аналитически:
Max (min) =max (21; 22) =22
Min (max) =min (70; 49) =49
α =22; β =49
Так как α 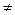 β , то отсюда следует, что седловой точки нет и игра решается в смешанных стратегиях.
β , то отсюда следует, что седловой точки нет и игра решается в смешанных стратегиях.
22 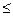 γ
γ 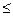 49
49
А – игрок 1, В – игрок 2.
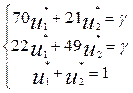 =>
=> 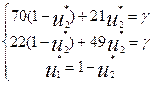
70 (1- 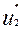 ) + 21
) + 21 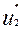 = 22 (1-
= 22 (1- 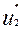 ) + 49
) + 49 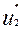
70 - 70 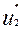 + 21
+ 21 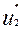 = 22 - 22
= 22 - 22 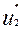 + 49
+ 49 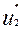
-49 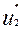 -27
-27 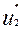 = 22 -70
= 22 -70
-76 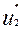 = -48
= -48
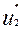 =
= 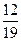
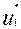 = 1-
= 1- 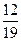 =
= 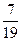
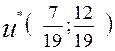 - оптимальная стратегия первой компании А
- оптимальная стратегия первой компании А
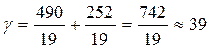
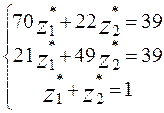 =>
=> 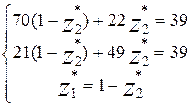
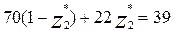
-48 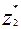 =-31
=-31
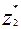 = 0,63
= 0,63
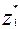 = 0,37
= 0,37
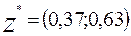 - оптимальная стратегия второй компании В
- оптимальная стратегия второй компании В
Средняя величина прибыли при любом состоянии спроса равна 39 денежных единиц объема выпуска каждой модели. Смешанная стратегия первой компании 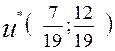 , смешанная стратегия второй компании
, смешанная стратегия второй компании 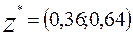 .
.
5.2. Решим игру сведением к задаче линейного программирования.
Составим пару взаимно двойственных задач:
(1) f = 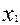 +
+ 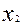
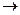 max (2) f =
max (2) f = 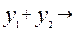 min
min
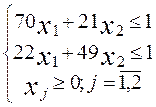
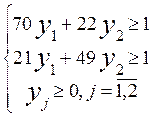
Приведем задачу к каноническому виду:
f= 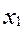 +
+ 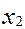 +0*
+0* 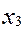 +0*
+0* 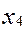
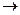 max
max
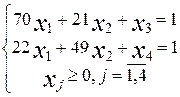
строим симплексную таблицу:
| Шаг 0 | |||||
| Базис | БП | x 1 | x 2 | x 3 | x 4 |
| x3 | |||||
| x4 | |||||
| ИС | -1 | -1 | |||
| Шаг 1 | |||||
| Базис | БП | x 1 | x 2 | x 3 | x 4 |
| x1 | 1/70 | 3/10 | 1/70 | ||
| x4 | 24/35 | 212/5 | -11/35 | ||
| ИС | 1/70 | -7/10 | 1/70 | ||
| Шаг 2 | |||||
| Базис | БП | x 1 | x 2 | x 3 | x 4 |
| x1 | 1/106 | 7/424 | -3/424 | ||
| x2 | 6/371 | -11/1484 | 5/212 | ||
| ИС | 19/742 | 27/2968 | 7/424 |
Решение игры:
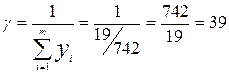
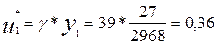
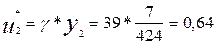
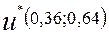
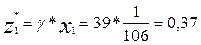
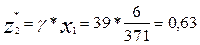
5.3.
| переменные | ||||||
| имя | Х1 | Х2 | ||||
| Значение | 0,009434 | 0,016173 | ЦФ | Направл. | ||
| ЦФ | 0,025606 | max | ||||
| ограничения | ||||||
| вид | лев часть | знак | прав часть | |||
| Огран.1 | <= | |||||
| Огран.2 | <= |
5.4. Все найденные решения одинаковы.
5.5.Чтобы компании получили среднюю прибыль равную 39 рублей, фирма А должна рекламировать 36% своего товара по радио и 64 % в газетах, фирма В 37% на телевидении и 63 % рассылает брошюры по почте.
5.6. Решение задачи аналитически, в симплексе и в Excel дает одинаковый результат. Делаем вывод, что задача решена правильно.
5.7.
| Отчет по результатам | ||||||
| Целевая ячейка (Максимум) | ||||||
| Ячейка | Имя | Исходное значение | Результат | |||
| $D$4 | ЦФ ЦФ | 0,025606469 | ||||
| Изменяемые ячейки | ||||||
| Ячейка | Имя | Исходное значение | Результат | |||
| $B$3 | Значение Х1 | 0,009433962 | ||||
| $C$3 | Значение Х2 | 0,016172507 | ||||
| Ограничения | ||||||
| Ячейка | Имя | Значение | Формула | Статус | Разница | |
| $D$8 | Огран.1 лев часть | $D$8<=$F$8 | связанное | |||
| $D$9 | Огран.2 лев часть | $D$9<=$F$9 | связанное |
| Отчет по устойчивости | |||||||
| Изменяемые ячейки | |||||||
| Результ. | Нормир. | Целевой | Допустимое | Допустимое | |||
| Ячейка | Имя | значение | стоимость | Коэффициент | Увеличение | Уменьшение | |
| $B$3 | Значение Х1 | 0,009433962 | 2,333333333 | 0,551020408 | |||
| $C$3 | Значение Х2 | 0,016172507 | 1,227272727 | 0,7 | |||
| Ограничения | |||||||
| Результ. | Теневая | Ограничение | Допустимое | Допустимое | |||
| Ячейка | Имя | значение | Цена | Правая часть | Увеличение | Уменьшение | |
| $D$8 | Огран.1 лев часть | 0,009097035 | 2,181818182 | 0,571428571 | |||
| $D$9 | Огран.2 лев часть | 0,016509434 | 1,333333333 | 0,685714286 |
| Отчет по пределам | |||||||||
| Целевое | |||||||||
| Ячейка | Имя | Значение | |||||||
| $D$4 | ЦФ ЦФ | 0,025606469 | |||||||
| Изменяемое | Нижний | Целевой | Верхний | Целевой | |||||
| Ячейка | Имя | Значение | предел | результат | предел | результат | |||
| $B$3 | Значение Х1 | 0,009433962 | 0,016172507 | 0,009433962 | 0,025606469 | ||||
| $C$3 | Значение Х2 | 0,016172507 | 0,009433962 | 0,016172507 | 0,025606469 |
