Частотный критерий устойчивости Попова

Рассмотрим нелинейные системы, структурные схемы которых можно привести к виду, показанному на рисунке 3.5. В этой структурной схеме имеется безынерционный нелинейный элемент с характеристикой

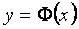(3.21)

и линейная часть с передаточной функцией W (s), имеющей статический коэффициент передачи, равный единице, и импульсной переходной функцией 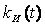.Все воздействия приведены к одному входу и обозначены .

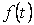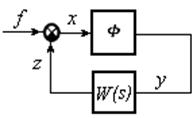
Рисунок 3.5 - Структурная схема системы с безынерционным нелинейным элементом

Изображение решения дифференциального уравнения системы выразим через изображения воздействия F (s) и координаты :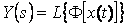

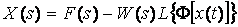. (3.22)

Переходя к оригиналам, получаем интегральное уравнение Вольтерра второго рода:

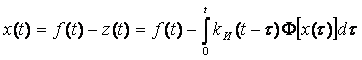. (3.23)

Будем рассматривать систему при таких воздействиях, кото­рые ограничены по модулю и являются исчезающими функциями времени. Обозначим максимальное воздействие 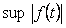(supremum).

Исчезающей функцией времени 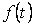назовем функцию, стремя­щуюся с течением времени к нулю:

.

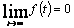Если воздействие отсутствует, то из (3.23) следует

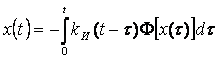. (3.24)

Если нелинейная характеристика проходит через начало координат, т. е. Ф(0)=0, то уравнение (3.24) имеет тривиаль­ное решение:

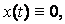(3.25)

которое соответствует положению равновесия.

Положение равновесия устойчиво в смысле Ляпунова, если существует такое положительное число 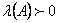, что при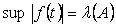

имеет место неравенство 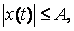(3.26)

где А — сколь угодно малое положительное число.

В зависимости от того, при каких значениях 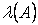выпол­няется неравенство (3.26) будем различать три вида устойчивости: устойчивость в малом, если 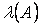бесконечно малая величина; устойчивость в большом, если 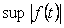- конечная величина, и устойчивость в це­лом, если не ограничено.

Изложим ча­стотный метод определения устойчивости, предложенный В. М. Попо­вым [5], при использовании которого задача решается более просто приемами, аналогичными частотным способам ис­следования устойчивости линейных систем.

Если в системе автоматического регулирования имеется лишь одна однозначная нелинейность

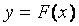, (3.27)

то, объединив вместе все остальные (линейные) уравнения системы, можно всегда получить общее уравнение линейной части системы (см. рисунок 3.6, а) в виде:

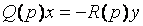, (3.28)

где ,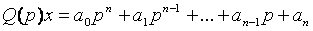

,

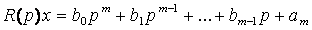причем будем считать т < п.

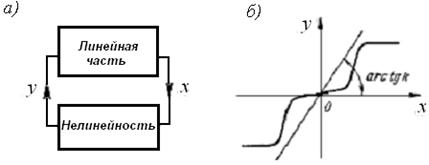
Рисунок 3.6 - Система автоматического регулирования с однозначной нелинейностью

Пусть нелинейность y=F(x) имеет любое очертание, не выходящее за пределы заданного угла arctg k (см. рисунок 3.6, б), т. е. при любом х,

0< F(x)< kx. (3.29)

Пусть многочлен Q(p),или что одно и то же, характеристическое уравнение линейной части Q(p)=0, имеет все корни с отрицательными вещественными частями или же, кроме них, имеется еще не более двух нулевых корней. Другими словами, допускается, чтобы 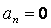или и 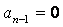в выражении Q(p),т. е. не более двух нулевых полюсов в передаточ­ной функции линейной части системы:

.

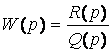Приведем без доказательства формулировку теоремы В.М.По­пова: для установления устойчивости нелинейной системы доста­точно подобрать такое конечное действительное число h, при котором при всех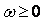

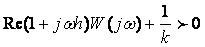, (3.30)

где 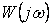- амплитудно-фазовая частотная характеристика линейной части системы.

При наличии одного нулевого полюса требуется еще, чтобы

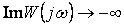при ,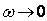

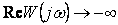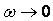а при двух нулевых полюсах при , a 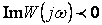при малых .

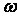Теорема справедлива также и при наличии в знаменателе Q(p) передаточной функции линейной части не более двух чисто мнимых корней, но при этом требуются некоторые другие простые добавочные условия [5], называемые условиями предельной устойчивости.

Другая формулировка той же теоремы, дающая удобную гра­фическую интерпретацию, связана с введением видоизмененной частотной характеристики 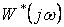, которая определяется следую­щим образом:

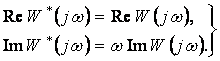
График 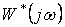имеет вид (см. рисунок 3.7, а), аналогичный 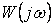, когда в выражениях Q(p) и R(p) разность степеней п- т>1. Если же разность степеней 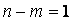, то конец графика 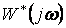будет на мнимой оси ниже начала координат (см. рисунок 3.7, б).

Далее, выполнив соответствующие математические преобразования, рассмотрим следующую графическую интерпретацию тео­ремы В. М. Попова.

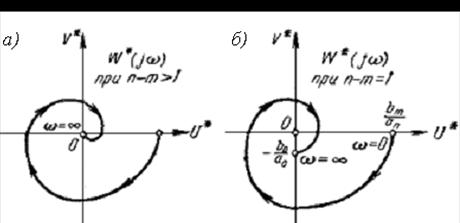
Рисунок 3.7 - Видоизмененные частотные характеристики 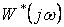к формулировке теоремы В. М. Попова

Преобразуем левую часть неравенства (3.30):

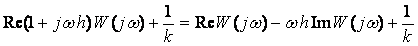. (3.31)

Тогда, положив

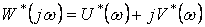
и использовав соотношение (3.31), получим вместо (3.30) для теоремы В. М. Попова условие:

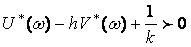(3.32)

при всех .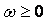

Очевидно, что равенство

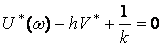(3.33)

представляет уравнение прямой на плоскости .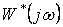

Отсюда вытекает следующая графическая интерпретация тео­ремы В. М. Попова: для установления устойчивости нелинейной системы достаточно подобрать такую прямую на плоскости 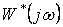, проходящую через точку 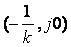, чтобы вся кривая 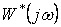лежала справа от этой прямой.

На рисунке 3.8 приведена графическая интерпретация тео­ремы В. М. Попова для установления устойчивости нелинейной системы. Как видно, рисунки 3.8, а и 3.8, б соответствуют устойчивым системам, а рисунки 3.8, в и 3.8, г – неустойчивым.

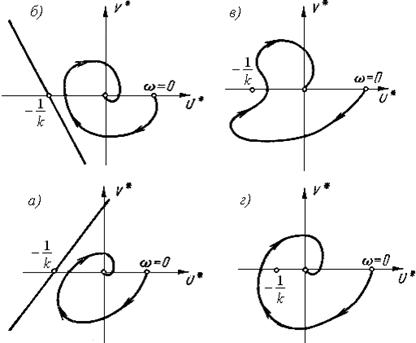
Рисунок 3.8 - Графическая интерпретация тео­ремы В. М. Попова для определения устойчивости нелинейной системы