Матрица парных коэффициентов корреляции
| У | 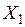 | 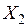 | … | 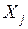 | … | 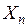 | |
| У | I |  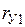 | 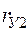 | … | 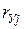 | … | 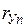 |
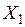 | 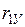 | I | 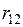 | … | 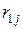 | … | 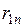 |
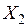 | 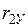 | 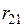 | I | … | 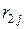 | … | 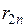 |
| … | … | … | |||||
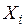 | 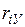 | 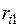 | 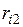 | … | 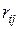 | … | 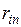 |
| … | … | … | |||||
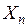 | 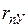 | 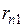 | 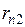 | … | 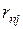 | … | I |
На основе корреляционной матрицы выявляются факторы, имеющие наиболее тесную связь с результативным признаком. Тем самым производится предварительный отбор факторов для включения их в модель. Корреляционная матрица также дает возможность определения мультиколлинеарности, которая имеет место в том случае, когда связь между факторами-аргументами превышает тесноту связи между данными аргументами и зависимыми признаками. Если одно из неравенств (при анализе двух факторов) 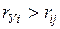 и
и 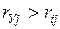 не выполняется, то для устранения мультиколлениарности следует исключить один из факторов, обычно тот, который менее тесно связан с результативным признаком.
не выполняется, то для устранения мультиколлениарности следует исключить один из факторов, обычно тот, который менее тесно связан с результативным признаком.
Таким образом, парные коэффициенты корреляции отражают тесноту связи между результативным признаком (У) и фактором-аргументом, например (Х), при одновременном косвенном влиянии других корреляционно с ним связанных факторов.
Дополнить парные коэффициенты корреляции можно расчетом частных. Частный коэффициент корреляции характеризует тесноту связи между результативным фактором (У) и данным фактором ( 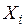 ) при элиминировании (исключении) связи У с другими факторами, включенными в модель.
) при элиминировании (исключении) связи У с другими факторами, включенными в модель.
Коэффициенты частной детерминации позволяют выявить роль каждого фактора, включенного в модель в объясненной вариации, допустим, коэффициент множественной детерминации составил 0,85.
Математически доказано, что он равен сумме коэффициентов частной детерминации. По фактору 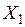 коэффициент частной детерминации равен
коэффициент частной детерминации равен 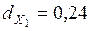 , по фактору
, по фактору 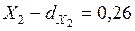 и
и 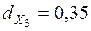 . В результате
. В результате 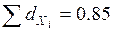 , т.е. благодаря корреляционному анализу удалось на 85 % объяснить вариацию результативного признака У, факторами вошедшими в модель. Одновременно выяснена роль каждого фактора - на 1-ом месте стоит фактор Х3 - на 35 % объясняющий вариацию результативного признака ит.д. Коэффициенты частной детерминации (
, т.е. благодаря корреляционному анализу удалось на 85 % объяснить вариацию результативного признака У, факторами вошедшими в модель. Одновременно выяснена роль каждого фактора - на 1-ом месте стоит фактор Х3 - на 35 % объясняющий вариацию результативного признака ит.д. Коэффициенты частной детерминации ( 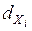 ) можно получить, используя парные коэффициенты корреляции (
) можно получить, используя парные коэффициенты корреляции ( 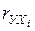 ) и
) и 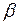 - коэффициенты (
- коэффициенты ( 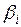 )
)
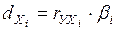 .
.
Таким образом, коэффициент частной детерминации равен произведению коэффициента парной корреляции на коэффициент 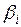 .
.
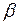 - коэффициенты имеют и самостоятельное значение при анализе модели. Они позволяют выразить коэффициенты регрессии в едином стандартизованном масштабе. Рассчитанные коэффициенты множественной регрессии несопоставимы между собой, т.к. зависят от единиц измерения соответствующих факторов. Но даже и в случае одноименных единиц измерения несопоставимость вызвана тем, что коэффициенты регрессии не учитывают степени вариации факторов. Для достижения сопоставимости коэффициентов регрессии исчисляют
- коэффициенты имеют и самостоятельное значение при анализе модели. Они позволяют выразить коэффициенты регрессии в едином стандартизованном масштабе. Рассчитанные коэффициенты множественной регрессии несопоставимы между собой, т.к. зависят от единиц измерения соответствующих факторов. Но даже и в случае одноименных единиц измерения несопоставимость вызвана тем, что коэффициенты регрессии не учитывают степени вариации факторов. Для достижения сопоставимости коэффициентов регрессии исчисляют 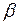 - коэффициенты
- коэффициенты
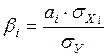 .
.
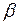 - коэффициенты показывают, на сколько средних квадратических отклонений (
- коэффициенты показывают, на сколько средних квадратических отклонений ( 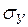 ) изменяется (У) при увеличении (
) изменяется (У) при увеличении ( 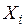 ), на одно среднеквадратическое отклонение (
), на одно среднеквадратическое отклонение ( 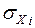 ) , при неизменности остальных факторов, входящих в модель.
) , при неизменности остальных факторов, входящих в модель.
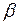 - коэффициенты можно использовать для выявления факторов, оказывающих наибольшее влияние с учетом их колеблемости на результативный признак. Фактор, имеющий наибольшее (по абсолютной величине) значение
- коэффициенты можно использовать для выявления факторов, оказывающих наибольшее влияние с учетом их колеблемости на результативный признак. Фактор, имеющий наибольшее (по абсолютной величине) значение 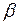 - коэффициента способен оказать наибольшее влияние, на исследуемый показатель.
- коэффициента способен оказать наибольшее влияние, на исследуемый показатель.
Во многих используемых программах корреляционно-регрессионного анализа на ЭВМ определяются частные коэффициенты эластичности. Коэффициенты эластичности устраняют различия в единицах измерения факторов и рассчитываются по формуле
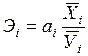 .
.
Частные коэффициенты эластичности показывают на сколько процентов изменяется в среднем зависимый показатель (У) при увеличении 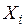 на 1 % при фиксированном положении других факторов.
на 1 % при фиксированном положении других факторов.
Если результативный показатель (У) увеличивается в большей степени, чем фактор( 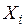 ), то
), то 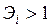 , если же У возрастает в меньшей степени, чем фактор, то
, если же У возрастает в меньшей степени, чем фактор, то 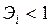 . Если
. Если 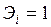 , то темпы прироста У и
, то темпы прироста У и 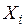 одинаковы. Сумму коэффициентов эластичности
одинаковы. Сумму коэффициентов эластичности 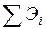 называют эластичностью производства. Для нее сохраняются те же соотношения. Например, если
называют эластичностью производства. Для нее сохраняются те же соотношения. Например, если 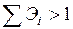 , то с увеличением всех факторов на один и тот же процент, зависимый показатель возрастает в большей степени, чем факторы.
, то с увеличением всех факторов на один и тот же процент, зависимый показатель возрастает в большей степени, чем факторы.
Применение средств электронно-вычислительной техники существенно облегчает проведение корреляционного анализа, поскольку задача исследователя сводится к правильному формированию исходной информации, реализации алгоритма решения на конкретной ЭВМ, а так расшифровке и интерпретации результатов расчетов.
Основные правила формирования исходной информации изложены в разделе 2,1;машинная реализация алгоритма (последовательность и правила выполнения операций по решению задачи на ЭВМ) даны в соответствующих инструкциях к машинам, а также методических пособиях.
Расшифровку и интерпретацию результатов рассмотрим на конкретном примере.
Пример. Выявить влияние качества пашни и дозы внесения минеральных удобрений на урожайность зерновых на основе данных наблюдений по модельным хозяйствам Ставропольского края.
Согласно приведенным рекомендациям, исходные данные представляем в виде матрицы исходных данных (таблица 16). Они должны быть введены в ЭВМ.
Для контроля операций рекомендуется вывод всех промежуточных результатов не только на экран дисплея, но и на печатающее устройство. Это существенно облегчает построение и анализ корреляционной модели, а также дает возможность для последующего расчета ряда дополнительных статистических показателей.
Отпечатанные выходные параметры по программе “KRА” из пакета «РРР» состоят из 4-х разделов: “Исходные данные для регрессионного анализа”; “Корреляционно-регрессионный анализ”; “Статистические характеристики”; “Анализ взаимосвязей”.
Таблица 16
