Несменяемое рабочее тело
В замкнутом цикле рабочее тело несменяемое. Оно получает теплоту от внешнего горячего источника, переходит в цилиндр, совершает работу. После этого рабочее тело сжимается в цилиндре и передается холодному источнику для отвода теплоты. После обновления состояния рабочее тело снова пригодно к совершению цикла. В качестве рабочего тела в реальном двигателе с внешним подводом теплоты обычно используют газы с высокой текучестью и теплоемкостью (гелий или водород). Рабочее тело своим химическим составом в процессах тепловыделения не участвует. Особенности процессов сообщения рабочему телу свободной энергии и отвода теплоты таковы, что для обеспечения эффективности процесса горячий и холодный источник должны быть термоизолированы друг от друга. Поэтому в замкнутых циклах невозможно обеспечить внутренние процессы подвода и отвода теплоты. В случае если расположить горячий и холодный источники внутри цилиндра, теплота, минуя рабочее тело, напрямую будет переходить от горячего источника к холодному источнику.
В разомкнутом цикле процесс передачи теплоты рабочему телу внутренний. Топливо – носитель энергии смешивается с воздухом внутри цилиндра. Происходит процесс сгорания и тепловыделения. При этом часть выделившейся энергии отводится в стенки цилиндра, другая ее часть преобразуется в работу. В таком процессе рабочее тело для повторного использования не пригодно, т.к. содержащийся в нем кислород выгорел. Для повторения цикла продукты сгорания необходимо удалить из цилиндра и подать туда свежий воздух.
Как видно из описания, сменяемость или несменяемость рабочего тела характеризует не просто процесс тепловыделения, а характеризует способ подвода теплоты. Если мы утверждаем, что рабочее тело в цикле является постоянным, то тем самым утверждаем, что в цикле осуществляется подвод теплоты от внешнего горячего источника и отвод теплоты внешнему холодному источнику. Если же мы утверждаем, что рабочее тело сменяемое, то тем самым мы утверждаем, что в цикле осуществляются внутренние процессы подвода и отвода теплоты.
Поэтому, если, анализируя разомкнутый цикл, мы принимаем допущение о том, что рабочее тело в цикле является постоянным, то независимо от дальнейших наших рассуждений, мы фактически вынуждены рассматривать, анализировать и рассчитывать процессы цикла с внешним подводом и отводом теплоты.
Принятие допущения о несменяемости рабочего тела заставляет заменить процесс удаления рабочего тела процессом отвода теплоты. С позиций второго закона термодинамики процесс отвода работы потребителю и процесс отвода теплоты компенсации холодному источнику являются равнозначными, обязательными и неотъемлемыми функциями процесса преобразования теплоты в работу. Данные процессы один без другого существовать не могут. Поэтому, если теория считает возможным изъять процесс отвода теплоты из процесса преобразования теплоты в работу и заменить им процесс удаления рабочего тела, в порядке эксперимента можно заменить процесс удаления рабочего тела процессом отвода работы. В этом случае нелепость такой замены сразу становится очевидной. А между тем с точки зрения второго закона термодинамики оба варианта замены одинаково равноценны и абсурдны.
В результате такой замены часть теплоты компенсации автоматически приплюсовывается к теплоте превращенной в работу. Т.е. закладывается не только ложная основа для дальнейших расчетов, но и с точки зрения формальной термодинамики цикл превращается в фикцию. Оказывается, что преобразование теплоты в работу возможно и путем фиктивной подмены одного необязательного процесса (удаления рабочего тела) другим обязательным процессом (отводом теплоты компенсации холодному источнику).
Из изученной литературы видно, что теория при расчетах интенсивных (и экстенсивной) величин (Р, V и Т) параметров рабочего тела разомкнутых циклов пользуется правилами расчета замкнутого цикла, в котором термический КПД выше. В результате этого расчетные величины оказываются существенно больше, чем реальные. То есть, при переходе от замкнутого идеального цикла к разомкнутым термодинамическим циклам, вопреки первому закону термодинамики, в наличии оказывались неизвестно откуда взявшиеся излишки теплоты. Для объяснения этого непонятного явления придумывались целые теории, а излишки теплоты списывались на какие-либо вымышленные процессы.
Ближе всех к разгадке этого теоретического феномена подошел И.М.Ленин.
«Если бы двигатель имел только потери тепла, определяемые вторым законом термодинамики, то соответствующие удельные расходы топлива в зависимости от степени сжатия (при работе на стехиометрической смеси) определялись бы следующими данными:
Таблица 23-а
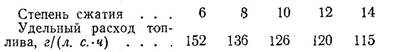
(И.М. Ленин, стр.143 т.1)
В действительности тепловые потери примерно на 20% больше, вследствие чего расходы топлива на индикаторную силу в час выше».
(Комментарий: «Потери тепла, определяемые вторым законом термодинамики» И.М. Ленин рассчитывает исходя из формулы ht =1- 1/εk-1. Но данная формула при расчете разомкнутого цикла определяет лишь потери теплоты уносимой выпускными газами. «В действительности тепловые потери примерно на 20% больше» потому, что «потери тепла» разомкнутого цикла (в виде отвода теплоты холодному источнику), «определяемые вторым законом термодинамики» данной формулой просто не учитываются).
«Термический КПД теоретического разомкнутого цикла представляет собой отношение тепла, превращенного в работу, к затраченному теплу:
ht раз=1- Q2 раз/ Q1= 1- q2 раз,
где Q1- тепло, которое может выделиться при полном сгорании топлива: Q2 раз-тепло, которое не может быть использовано в теоретическом разомкнутом цикле; это принципиально неустранимая потеря теоретического цикла.
Термический КПД разомкнутого цикла htраз меньше, чем термический КПД замкнутого цикла ht, примерно на 25% и также зависит от степени сжатия двигателя, что иллюстрируется следующими данными:
Степень сжатия.................. 6 8 10
ht замкнутого цикла%51 56,5 60
ht раз разомкнутого цикла%39,5 44 47,5
ht раз/ht 0,77 0,78 0,79»
(И.М. Ленин, стр. 182-183, т.1).
Как следует из описания, «разомкнутый цикл» И.М. Ленина отличается от термодинамического замкнутого цикла только одним признаком: в «разомкнутом цикле» из-за большей теплоемкости трехатомных газов рабочее тело якобы уносит с собой больше теплоты, чем это можно было бы себе представить. Но как далее следует из учебника, при дальнейших расчетах эта особенность «разомкнутых циклов» И.М. Лениным учитывалась через значения показателей адиабаты и политропы, и никакого влияния на излишки тех 20% теплоты не оказывала.
Поскольку такая «разомкнутость» явно не объясняла причин расхождения в количествах теплоты в тепловом балансе цикла, И.М. Ленин указывает еще на одну возможную причину- химическую неполноту сгорания.
Как видно из таблицы И.М. Ленин считает, что в бензиновом двигателе полностью не сгорает 20% топлива и еще 7% (остаточный член qост) появляется из ничего и исчезает в никуда.
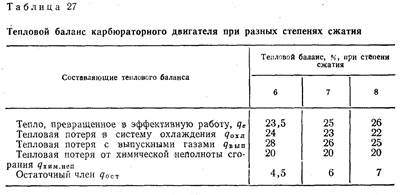
(И.М.Ленин, стр. 195, т.1)
Д.Н. Вырубов (стр. 165-166) подошел к решению этого вопроса чуть по- иному:
«Неполное использование теплоты сгорания топлива возможно не только в результате недостатка воздуха, но также вследствие диссоциации продуктов сгорания. Явление диссоциации состоит в расщеплении молекул продуктов сгорания, сопровождающееся поглощением теплоты», т.е. он указывает на возможность неполного использования теплоты из-за диссоциации. И указывает на способ решения задачи:
«Предпосылка мгновенного сгорания топлива при постоянном объеме определяет получение при расчете по формуле (192) завышенного максимального давления цикла. Для уточнения значения действительного максимального давления рz¶ с учетом теплоотдачи в период сгорания и конечной длительности этого периода вводят поправочный множитель φр и определяют действительное максимальное давление цикла
рz¶= рz φр. (193)
Коэффициент уменьшения давления φр = 0.8 ÷ 0.9». (Подчеркнуто мной).
Следовательно, тоже подтверждает факт появления излишков теплоты. Но, не вдаваясь в подробности, откуда они появились, путем использования поправочного множителя расчеты избавляются от лишнего количества теплоты, и, соответственно, уменьшается завышенная величина термического КПД.
Приведенные варианты решений не вскрывают причин возникновения проблемы, а лишь заметают ее следы, вызывая новые вопросы. Поправочный множитель, множитель уменьшения количества теплоты из-за изменения молекулярной массы, неполнота сгорания, диссоциация и пр. сами по себе выражения неплохие и в какой-то мере загадочные. Согласно первому закону термодинамики теплота (энергия) из ничего не может появиться и в ничто не может превратиться. Применять такие множители можно, но при этом должно быть объяснено: из чего возникли излишки теплоты и куда они делись. Если произошла диссоциация, выхлопные газы должны быть более горячими на соответствующее количество температуры. Если считать, что неполнота сгорания может быть до 20% от общего количества смеси, то и выхлопные газы должны содержать суммарно не меньше 40% СО, СН и NОх.
Применение поправочного коэффициента позволяет только математически свести баланс, но не объясняет того, почему в цикле появилось лишнее количество теплоты, и куда она потом реально уводится.
(Комментарий: Попытки выяснить причину расхождения между термическими КПД идеального цикла и теоретических циклов предпринимались многими теоретиками. Была создана методика сравнения параметров циклов. В частности, связь между ht и hi установили через относительный КПД hо, учитывающий все потери в действительном цикле, не учитываемые в идеальном цикле (см. монографию Д.А. Портнова «Турбопоршневые двигатели»). Согласно этой теории ht = hi. hо).
Разомкнутые циклы отличаются от замкнутого именно признаком удаления и обновления рабочего тела со всеми вытекающими из этого отличия последствиями. Принятие допущения о несменяемости рабочего тела означает, что мы лишаем цикл основного его отличительного признака и даем описание замкнутого цикла.
Для наглядности составим описание циклов согласно принятым в теории допущениям: 1. Замкнутый цикл Стирлинга - термодинамический цикл по преобразованию теплоты в работу с адиабатными процессами сжатия и расширения, подводом и отводом теплоты по изохорам. 2. Разомкнутый цикл Бо Де Роша - термодинамический цикл по преобразованию теплоты в работу с адиабатными процессами сжатия и расширения, подводом и отводом теплоты по изохорам.
То есть, согласно данному описанию цикл Бо Де Роша тоже является замкнутым. Чтобы описание цикла Бо Де Роша соответствовало признакам разомкнутого цикла оно должно быть составлено следующим образом: термодинамический цикл по преобразованию теплоты в работу с подводом теплоты по изохоре, с отводом теплоты на политропном процессе сжатия, с адиабатным процессом расширения и обновлением рабочего тела по изохоре.
Главной задачей анализа термодинамических замкнутых циклов является выявление того, какое количество теплоты будет превращено в работу (1), и какое количество теплоты будет отведено холодному источнику (2), при протекании процесса преобразования теплоты в работу.
Главной задачей анализа термодинамических разомкнутых циклов является выявление того, какое количество теплоты будет превращено в работу (1), какое количество теплоты будет отведено холодному источнику (2) при протекании процессапреобразования теплоты в работу, и какое количество остаточной теплоты будет удалено из системы (3) по завершении процесса преобразования теплоты в работу.
В связи с приведенными утверждениями необходимо следующее пояснение: особенности цикла (т.е. является ли цикл замкнутым или разомкнутым) определяют и особенности термодинамической системы, в которой он происходит. Эта особенность указанных систем обуславливает принципиальные отличия между ними в вопросах о том: 1. Какое количество теплоты можно сообщить рабочему телу, находящемуся в системе. 2. Как эта теплота используется системой.
Рабочему телу в замкнутой системе можно сообщить относительно небольшое количество теплоты Qv (символ Qv означает, что рассматривается система, в которой совершается замкнутый цикл V=const). Но при этом вся подведенная рабочему телу теплота делится на 2 части: одна часть Qv1 преобразуется в работу, вторая часть Qv2 отводится холодному источнику.
Замкнутая термодинамическая система не сообщается с окружающей средой и по принимаемым допущениям (источник теплоты, рабочее тело, холодильник и потребитель работы) содержит в себе все необходимые условия для преобразования теплоты в работу. Термический КПД такой системы равен 1 или 100%.
Рабочему телу в разомкнутой системе можно сообщить значительно большее количество теплоты Qраз. или свободной энергии F1. При этом эта теплота присоединяется к энтропии рабочего тела имеющего температуру Та или к связанной энергии F2. Количество используемой (обращаемой) в цикле энергии становится равным F= F1 + F2. При протекании цикла и в момент его завершения обращаемая в цикле теплота окажется разделенной на 3 части: Qобр1 преобразуется в работу, Q обр2 отводится холодному источнику и Q обр3 удаляется в окружающую среду.
Разомкнутая термодинамическая система в момент окончания процесса преобразования теплоты в работу «открывается», сообщается с окружающей средой, удаляя туда рабочее тело с частью теплоты, которую цикл не смог преобразовать в работу и отвести холодному источнику. По завершении процесса удаления система принимает из окружающей среды новое рабочее тело, которое содержит в себе значительно меньшее количество энергии, чем удаленное из системы рабочее тело. Данный процесс в теории назван процессом обновления рабочего тела, что соответствует его сути и смыслу. Повторимся еще раз: в этом процессе от рабочего тела теплота не отводится, а рабочее тело удаляется из системы с остаточной энергией цикла. Отношение количества обращаемой теплоты Q обр к количеству теплоты Q обр3, уносимого рабочим телом составит термический КПД разомкнутой термодинамической системы (htt). Термодинамический (или термический) КПД разомкнутой системы вычисляется формулой htt =1- 1/εk-1, в которой величина htt составляет количество теплоты, используемой для преобразования в работу и отвода холодному источнику, и величина 1/εk-1 составляет количество остаточной теплоты, уносимой рабочим телом в окружающую среду.
В действующей теории ДВС КПД цикла с подводом теплоты при V=const независимо от того является он замкнутым или разомкнутым определяется формулой ht =1- 1/εk-1. Считается, что термический КПД и замкнутого и разомкнутого циклов со степенью сжатия ε=10 при k=1.4 ht =60.17%.Но указанная формула может быть применена только к замкнутому циклу, в котором рабочее тело остается в системе со своей внутренней энергией, остающейся в нем после отвода теплоты. В балансах теплоты разомкнутых циклов учитывается, что рабочее тело поступает в систему при температуре Та и все расчеты теплоты производятся на основе Та. Затем при выведении разницы количеств теплоты преобразованной в работу и отведенной холодному источнику через интервал температур Тb -Та и Тz –Тс мы получаем результат по шкале Цельсия, а не Кельвина (например: 3000К – 2730К= 170С).
Согласно термодинамике теплота, как способ передачи энергии может быть получена, как от горячего источника, так и от холодного источника. Но в циклах тепловых машин горячий источник может только отдавать теплоту, а холодный источник может только поглощать ее. Соответственно, в зависимости от температуры субъектов процесса происходит деление теплоты на две категории: 1. Теплота- как тепло. 2. Теплота- как холод. Теоретической границей разделения «тепла» и «холода» является 00 С. Соответственно этому, рабочее тело с температурой 00 С в циклах тепловых машин обладает максимальной способностью принимать свободную энергию.
В циклах тепловых машин энергия сообщаемая рабочему телу сверх величины температуры Та является свободной энергией и теоретически только она может быть преобразована в работу и в теплоту компенсации. Поэтому, если рабочее тело остается в системе, расчеты, завершающиеся учетом температуры по шкале Цельсия, соответствуют действительности и формула ht =1- 1/εk-1 верна как для замкнутой термодинамической системы, так и для замкнутого цикла. Но если рабочее тело удаляется из системы, то энтропия удаляемого рабочего тела должна рассчитываться с учетом температуры по шкале Кельвина. Поскольку при выведении разницы температур результат всегда выходит по шкале Цельсия, указанная особенность разомкнутых термодинамических систем и циклов должна учитываться формулой ht =1- Q обр2+ Q обр3/Q обр, или формулой ht = 1- 1/e k-1 – Та/Тz.
В теории отсутствует разграничение между понятиями теплоты отводимой холодному источнику и теплоты компенсации. Под понятиями теплоты компенсации, теплоты отводимой холодному источнику и теплоты удаляемой с рабочим телом понимается одно и то же термодинамическое явление: это якобы часть теплоты, которая на основе второго закона термодинамики при протекании процесса преобразования теплоты в работу передается в виде компенсации холодному источнику. Анализ данного момента привел нас к выводу о том, что перечисленные понятия имеют разную сущность и содержание. Это видно на следующем примере: рассмотрим цикл на рис. 3 и рассчитаем два варианта параметров: 1). ε=51→ Тb1 =7910 К. 2). ε=5→ Тb2 = 15880 К. Если исходить из теории, в цикле со степенью сжатия ε=5 внутренняя энергия рабочего тела при температуре Тb2 = 15880 К есть теплота компенсации, отводимая холодному источнику. В цикле со степенью сжатия ε=51 количество теплоты, отводимой холодному источнику и, соответственно теплоты компенсации, меньше на величину 7970 С. Получается, что в цикле со степенью сжатия ε=51 мы дополнительно преобразовали в работу часть от той теплоты, которую в цикле со степенью сжатия ε=5, приняли за теплоту компенсации. Однако этого не может быть, поскольку термодинамика утверждает, что теплота компенсации принципиально не может быть использована для преобразования в работу. Следовательно, в замкнутом цикле с ε=5 из теплоты, отводимой холодному источнику, как минимум, часть ее, эквивалентная температуре 7970 С, является свободной энергией.
Теплоту, удаляемую с рабочим телом в окружающую среду, теория тоже считает теплотой компенсации. Но в комбинированных двигателях с продолженным расширением часть теплоты выпускаемых газов преобразовывается в работу. Раз ее можно превращать в работу, значит, и часть энергии удаляемых газов не является теплотой компенсации, а является свободной энергией.
Чтобы решить вопрос о том, как определить, что такое свободная- не использованная циклом энергия и что такое теплота компенсации обратимся к анализу «цикла» Карно (рис. 1).

 Р Q=Q1+Q2
Р Q=Q1+Q2


 Р1 а Q1=L А
Р1 а Q1=L А
 Т1 L L1
Т1 L L1

 L2
L2


 Р2 в
Р2 в
 Р4 d L1 L2
Р4 d L1 L2

 Т2
Т2
c
Q2 Р3
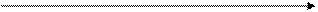
Рис. 1 V
Тепловой баланс «цикла» Карно: На участках cd и dа совершается работа сжатия в результате чего в точке а внутренняя энергия рабочего тела равна сумме работ L1+L2 при температуре Т1. На участке ав к рабочему телу подводится теплота в количестве Q. В точке в количество всей сообщенной рабочему телу энергии составит Q+L1+L2. На участке ав одновременно извлекается и передается потребителю работа L эквивалентная количеству теплоты Q1. Одновременно с этим аккумулятору системы А (допустим маховику) передается количество работы L1. При этом Q=L+L1. На участке вс совершается адиабатное расширение и аккумулятору системы А передается работа расширения L2. Температура рабочего тела в результате адиабатного расширения уменьшается от величины Т1 до величины Т2. На участке сd за счет работы L1, получаемой от аккумулятора А совершается изотермное сжатие рабочего тела при температуре Т2. От рабочего тела отводится теплота в количестве Q2. На участке dа за счет получаемой от аккумулятора А работы L2 совершается работа адиабатного сжатия. Температура рабочего тела поднимается от величины Т2 до величины Т1. Таким образом, в результате совершения цикла система должна выдать потребителю работу L эквивалентную теплоте Q1, от системы должна быть отведена теплота Q2.
Условия работы гипотетического двигателя Карно: Чтобы привести в действие, рабочему телу в термодинамической системе Карно необходимо сообщить энергию в виде работы сжатия, которая создает давление Р1 и температуру Т1. Далее система совершает работу за счет давления. При совершении работы давление Р1 (вследствие расширения) и температура Т1 (вследствие охлаждения) будут стремиться к уменьшению. В замкнутом расширяющемся сосуде давление создается температурой. Подводимая теплота полностью компенсирует уменьшение температуры и тем самым частично компенсирует уменьшение давления. Поэтому, если рассматривать процесс подвода теплоты и совершения работы не в целом, а конкретный механизм использования теплоты в каждой точке процесса, то окажется, что работа, совершаемая системой на изотермном участке ав, складывается из двух составляющих: 1. Работы L1 сообщенной рабочему телу на участке сжатия cd. 2. Работы L, получаемой в результате преобразования подводимой теплоты в количестве Q1 в давление (через температуру). В сумме два вида этих работ эквивалентны подводимой теплоте Q.
То есть, «внутренняя энергия и энтальпия идеального газа в изотермном процессе не изменяются, поэтому вся теплота, подведенная к газу, расходуется на совершение работы». («Теплотехника», стр. 44).
Что касается подводимой теплоты Q, то: 1. Часть подводимой теплоты в количестве Q1 расходуется на совершение работы. 2. Вторая часть теплоты в количестве Q2 безвозвратно (что принципиально неустранимо) расходуется на компенсацию температуры рабочего тела. При этом:
1. Если изотермное расширение продолжится до выравнивания давлений Рb=Ра, то при завершении процесса внутренняя энергия рабочего тела будет состоять только из температуры Т1, заключенной в объеме Vх при давлении Рх=Ра и рабочее тело больше не способно совершать работу. Для того, чтобы вернуть рабочему телу способность совершать работу необходимо обновить его состояние, т.е. подвергнуть сжатию с отводом от него теплоты компенсации до достижения температуры Т2.
2. В «цикле» Карно по завершении подвода теплоты (предварительного расширения) и уменьшения давления от величины Р1 до величины Р2 на участке вс производится последующее адиабатное расширение рабочего тела с отводом работы L2 в аккумулятор системы и уменьшением давления от величины Р2 до величины Р3. За счет расширения температура рабочего тела уменьшается до величины Т2. На изотермном участке сd путем подвода работы L1 от аккумулятора системы совершается сжатие рабочего тела с отводом теплоты в количестве Q2. В результате этого температура остается равной величине Т2, а давление увеличивается до величины Р4. Отведенная на этом участке теплота Q2 будет равна количеству теплоты, израсходованной на компенсацию температуры рабочего тела при совершении работы на участке ав. Если на изотермном участке сd не отвести теплоту Q2, то кривая давления окажется не в точке d,а выше этой точки, и цикл потеряет способность к совершению работы. При сжатии же с отводом теплоты в цикле изображенном на рис. 5 давление (поскольку п1 = 1) в точке d будет в 4.26 раз больше чем в точке с. При этом в точке d мы имеем качественно новое термодинамическое состояние рабочего тела, хотя внутренняя энергия и энтальпия рабочего тела не изменились.
«…внутренняя энергия идеального газа зависит только от температуры.
Внутренняя энергия и энтальпия являются функциями состояния, зависящими для идеального газа только от температуры» («Теплотехника», стр. 41).
То есть, в данной ситуации путем расчета энтропии рабочего тела через величину температуры Т2, мы не сможем определить насколько изменилось термодинамическое состояние рабочего тела от точки с до точки d и способно оно или не способно совершать работу. Для решения вопроса о том способно рабочее тело совершать работу или не способно необходимо установить, какую долю во внутренней энергии рабочего тела в точке d, составляет работа сжатия.
От точки d до точки а работой L2, получаемой из аккумулятора системы, совершается последующее адиабатное сжатие рабочего тела и температура рабочего тела изменяется от величины Т2 до величины Т1. От точки в до точки с совершается последующее адиабатное расширение рабочего тела с отводом в аккумулятор системы работы L2 и температура изменяяется от величины Т1 до величины Т2. При этом расчет количества работы L2 производится по формуле L2 = и1 – и2 = сυ (Т1 – Т2). («Теплотехника», стр. 45). То есть, разница температур Т1 – Т2 в данном цикле характеризует не количество совершаемой циклом работы за счет подведенной теплоты, а работу адиабатных участков сжатия и расширения, которые отношения к КПД цикла не имеют.
Таким образом: 1. Отвод теплоты от рабочего тела является необходимым условием для получения от него работы. То есть, если не отвести теплоту, рабочее тело не способно совершить работу. 2. При изотермном отводе теплоты происходит изменение интенсивного (давление) и экстенсивного (объем) параметров внутренней энергии рабочего тела. Путем уменьшения объема и увеличения давления, сопровождающегося отводом теплоты, производится замена связанной энергии (в виде температуры) на свободную энергии (в виде давления), но с позиций температуры Т2 в данном процессе никаких изменений не происходит. 3. При изотермном процессе сжатия количество отводимой теплоты Q2 равно количеству теплоты, компенсирующей температуру Т1 верхней изотермы. 4. Поэтому в изотермном процессе единственным фактором, определяющим КПД цикла (т.е. количество работы L цикла) является отношение величины подведенной теплоты Q к количеству отведенной теплоты Q2. 5. Интервал температур Т1 и Т2 и разница давлений Р2 и Р3 на участке вс позволяют рассчитать только количество работы L2, отводимой в аккумулятор системы и затем возвращаемой в цикл. Работа L2 является обращаемой энергией кругового процесса и никакого отношения к работе L и КПД цикла не имеет.
Вместе с тем модель «цикла» Карно является ключом к решению вопроса о том, как в других циклах определить, какая часть отводимой холодному источнику теплоты относится к теплоте компенсации, а какая часть относится к не использованной циклом свободной энергии.
Если в замкнутом цикле путем сжатия довести рабочее тело до способности полного использования свободной энергии и затем путем расширения до полной не способности совершать работу, то количество теплоты, которое необходимо отвести холодному источнику для возврата рабочего тела в исходное состояние (для восстановления первоначальной способности рабочего тела совершать работу) и есть теплота компенсации.
Пример замкнутого цикла V=Const: ε=60, k = 1.4, Та = 273 К, e k-1 = 5.1435, e k= 308.6, Рс=308.6 атм., Тс=14040 К, Рz =1049.3 атм., Тz =39040 К, Тb = 7590 К, Рb = 3.4 атм. Чтобы определить какое количество теплоты от внутренней энергии рабочего тела при Тb = 7590 К является теплотой компенсации необходимо продолжить расширение рабочего тела до величины Ра. Дополнительное расширение составит δ2 =2.4, давление конца расширения Рb =Ра, температура конца расширения Тb2 = 534.80 К и рабочее тело больше не способно совершать работу. Это означает, что с позиций второго закона термодинамики при совершении замкнутого цикла принципиально неустранимой потерей теплоты являются примерно 10.47% от подведенной теплоты. При совершении разомкнутого цикла принципиально неустранимой потерей теплоты являются примерно 19.29% от обращаемой теплоты, а остальное количество теплоты, отводимой холодному источнику, сверх указанного количества является свободной энергией, которая может быть преобразована в работу. То есть, из теплоты, отводимой холодному источнику, при приведенных выше параметрах Тb и Рb цикла со степенью сжатия ε=60 температура в количестве 224.20С эквивалентна количеству теряемой циклом свободной энергии, а теплота компенсации эквивалентна температуре 261.80 С. Соответственно, в цикле со степенью сжатия ε=5 (Тz =30190 К) энергия выпускаемых газов (Тb = 13150 С) состоит из теплоты компенсации, эквивалентной температуре 261.80 С, и свободной энергии, эквивалентной температуре 1053.20С. Поскольку в расчетных теоретических циклах удаляемое рабочее тело неизбежно содержит в себе и свободную энергию и теплоту компенсации, назовем энергию удаляемого рабочего тела при параметрах Тb и Рb остаточной теплотой цикла.
Это позволяет сделать вывод о том, что количество теплоты компенсации не зависит от степени сжатия цикла, а зависит только от количества подводимой теплоты. Степень сжатия цикла изменяет пропорции между количествами свободной энергии преобразуемой в работу и отводимой холодному источнику, т.е. определяет величину термического КПД цикла.
Следовательно, если в цикле с ε=5 теплота компенсации эквивалентна 261.80 С, а потери свободной энергии эквивалентны 1053.20С, то в цикле с ε=60 теплота компенсации эквивалентна 261.80 С, а потери свободной энергии эквивалентны 224.20С.
В любом цикле количество обращаемой энергии больше, чем количество свободной (подводимой) энергии. Из анализа «цикла» Карно видно, что для приведения системы в действие, к подводимой к рабочему телу теплоте Q необходимо добавить энергию работ сжатия L1 и L2, которые затем возвращаются в аккумулятор системы. В замкнутом цикле с процессом V=const помимо обращаемой в цикле работы сжатия в роли «добавленной» энергии выступает энтропия рабочего тела при температуре Та, которая по завершении цикла также остается в системе. Но в разомкнутом цикле «добавленная» энергия не остается в системе, а удаляется с выпускаемыми газами в окружающую среду. При составлении теплового баланса цикла указанный фактор оказывает существенное влияние на величину термического КПД. Поэтому, если в замкнутом цикле мы можем говорить о количестве свободной энергии цикла и вести расчет на его основе, то в разомкнутом цикле надо говорить о количестве обращаемой энергии цикла и вести расчет на его основе.
Для окончательного прояснения вопроса о том, что замкнутые и разомкнутые циклы отличаются друг от друга не просто формальными признаками, а по сути происходящих в них процессов, в порядке эксперимента снабдим «цикл» Карно процессом удаления рабочего тела. Предлагаем проанализировать рисунок 2.

 Р
Р

 а
а
Т1 Q раз

 Q раз1 (L)
Q раз1 (L)


 в
в

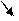 d
d

 c
c
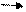 (Т3=Та) Q раз2 е Q раз3 (Т2=12690К)
(Т3=Та) Q раз2 е Q раз3 (Т2=12690К)

Рис. 2 V
