Вычисление поправок за центрировку и редукцию
| Назв. пункта | Назвнапр | M ° ¢ ² | M+ 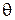 ° ¢ ² ° ¢ ² | M+ 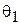 ° ¢ ² ° ¢ ² | S, м | c" | r" | ||||||
| 0,0 | 0,0 | +13,1 | |||||||||||
| 50,9 | 50,9 | +35,8 | |||||||||||
| 23,5 | 23,5 | +19,8 | |||||||||||
| 0,0 | 0,0 | +0,3 | |||||||||||
| 35,4 | 35,4 | -4,3 | |||||||||||
| 39,2 | 39,2 | -1,4 | |||||||||||
| 0,0 | |||||||||||||
| 27,4 | |||||||||||||
| 18,3 | |||||||||||||
| 0,0 | 0,0 | -0,2 | |||||||||||
| 23,1 | 23,1 | -0,1 | |||||||||||
| 16,6 | 16,6 | +0,1 | |||||||||||
| 0,0 | 0,0 | -1,4 | |||||||||||
| 4,0 | 4,0 | -0,3 | |||||||||||
| 15,9 | 15,9 | -0,4 | |||||||||||
| 0,0 | 0,0 | 0,0 | +1,2 | +55,5 | |||||||||
| 44,1 | 44,1 | 44,1 | +1,5 | +43,8 | |||||||||
| 0,9 | 0,9 | 0,9 | -0,3 | -34,6 | |||||||||
| 0,0 | 0,0 | +4,8 | |||||||||||
| 53,8 | 53,8 | +24,5 | |||||||||||
| 59,5 | 59,5 | +0,0 | |||||||||||
| 36,1 | 36,1 | -3,4 | |||||||||||
| 23,6 | 23,6 | -3,4 | |||||||||||
| 36,1 | 36,1 | -7,1 |
Вычисление поправки за кривизну изображения геодезической линии на плоскости в проекции Гаусса- Крюгера
В зависимости от заданной системы координат, в которой необходимо определить координаты пунктов, уравнивание выполняется на определенной поверхности. В нашем случае речь идет о Государственной системе координат, определенной в плоскости проекции Гаусса-Крюгера.
В связи с этим, необходимо исправить измеренные направления поправками за кривизну изображения геодезической линии на плоскости. Для этого необходимо вычислить приближенные координаты пунктов сети. Приближенные координаты вычисляют по формулам прямой геодезической задачи.
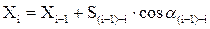 ,
,
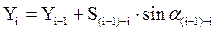 ,
,
где 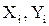 - координаты вычисляемого пункта;
- координаты вычисляемого пункта; 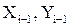 - известные координаты смежного пункта;
- известные координаты смежного пункта;  - расстояние между пунктами;
- расстояние между пунктами;  - дирекционный угол направления.
- дирекционный угол направления.
Вычисление приближенных координат пунктов сети выполняют в таблице 6. Если координата  исходного пункта представлена с учетом номера шестиградусной зоны (как в нашем случае – номер зоны равен одиннадцати), то при вычислении координат его (номер зоны) необходимо игнорировать. Для вычислений по пунктам триангуляции условно прокладывается теодолитный ход, исходной стороной которого является сторона с заданным дирекционным углом (сторона 2-3), исходным пунктом – пункт с известными координатами (пункт 2). При составлении хода необходимо предусмотреть контроль вычислений (в нашем случае ход замыкается на исходную сторону). В ходе вычисляются, как правило, «левые» углы (используется данные табл. 4). В нашем случае при составлении теодолитного хода для вычисления «левого» угла при вершине 3 необходимо значение угла в треугольнике II (рис.1.1) при соответствующей вершине вычесть из 360º и значение занести в соответствующую графу таблицы 6.
исходного пункта представлена с учетом номера шестиградусной зоны (как в нашем случае – номер зоны равен одиннадцати), то при вычислении координат его (номер зоны) необходимо игнорировать. Для вычислений по пунктам триангуляции условно прокладывается теодолитный ход, исходной стороной которого является сторона с заданным дирекционным углом (сторона 2-3), исходным пунктом – пункт с известными координатами (пункт 2). При составлении хода необходимо предусмотреть контроль вычислений (в нашем случае ход замыкается на исходную сторону). В ходе вычисляются, как правило, «левые» углы (используется данные табл. 4). В нашем случае при составлении теодолитного хода для вычисления «левого» угла при вершине 3 необходимо значение угла в треугольнике II (рис.1.1) при соответствующей вершине вычесть из 360º и значение занести в соответствующую графу таблицы 6.
Пример.
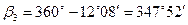
Углы и дирекционные углы округляются до одной угловой минуты, координаты вычисляются в километрах до третьего десятичного знака.
Расхождения дважды вычисленных значений координат не должны превышать 1 метра (пункт 2).
Таблица 6
| Вычисление приближённых координат пунктов | |||||||
| Пункт | Углы ° ΄ | Дир. Углы ° ΄ | Линии, км | 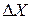 , км , км |  , км , км | X, км | Y, км |
| 6323,522 | 411,148 | ||||||
| 65 00 | 2.470 | +1.044 | +2.239 | ||||
| 347 52 | 6324,566 | 413,387 | |||||
| 232 52 | 2.663 | -1.608 | -2.123 | ||||
| 48 48 | 6322,958 | 411,264 | |||||
| 101 40 | 3.524 | -0.713 | +3.451 | ||||
| 260 23 | 6322,245 | 414,715 | |||||
| 182 03 | 2.245 | -2.245 | -0.080 | ||||
| 286 49 | 6320,000 | 414,635 | |||||
| 288 52 | 3.187 | +1.031 | -3.016 | ||||
| 212 46 | 6321,031 | 411,619 | |||||
| 321 38 | 2.024 | +1.587 | -1.256 | ||||
| 259 26 | 6322,618 | 410,363 | |||||
| 41 04 | 1.196 | +0.902 | +0.786 | ||||
| 203 58 | 6323,521 | 411,149 | |||||
| 65 02 | |||||||
 -87.553 Км -87.553 Км |
Поправки в прямое  и обратное
и обратное 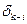 направления за кривизну изображения геодезической линии на плоскости в проекции Гаусса-Крюгера вычисляют по формуле:
направления за кривизну изображения геодезической линии на плоскости в проекции Гаусса-Крюгера вычисляют по формуле:
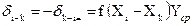 , (7)
, (7)
где  ,
,  – приближенные абсциссы пунктов,
– приближенные абсциссы пунктов, 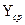 – среднее расстояние сети от осевого меридиана зоны, f - коэффициент, значение которого в триангуляции 1 разряда принято равным 0,00253. Поправки за кривизну изображения геодезической линии на плоскости вычисляют с точностью до 0.1² (табл.7).
– среднее расстояние сети от осевого меридиана зоны, f - коэффициент, значение которого в триангуляции 1 разряда принято равным 0,00253. Поправки за кривизну изображения геодезической линии на плоскости вычисляют с точностью до 0.1² (табл.7).
