Исходная модель и постановка задачи
В качестве примера рассмотрим модель возмущенных колебаний математического маятника
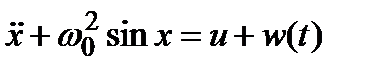
с управлением u и ограниченным внешним возмущением w (при произвольных углах отклонения от положения равновесия). Полагая
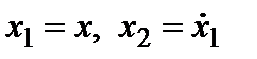 ,
,
приходим к системе
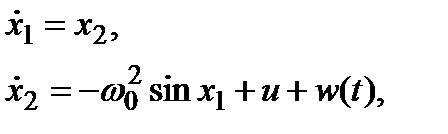 (1.1)
(1.1)
которую будем рассматривать как систему
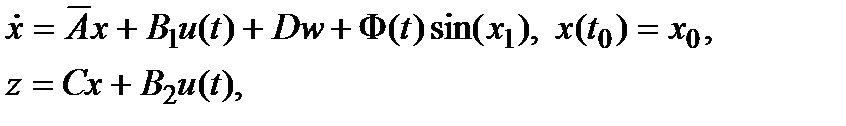 (1.2)
(1.2)
где 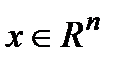 - вектор состояния,
- вектор состояния, 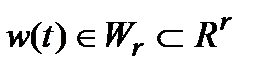 - входное возмущение,
- входное возмущение, 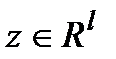 - вектор управляемого выхода,
- вектор управляемого выхода, 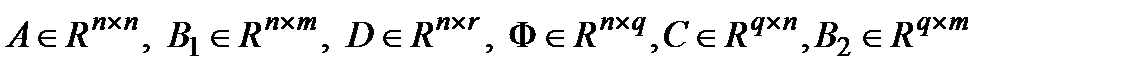 - известные постоянные матрицы,
- известные постоянные матрицы,  , T>t0 заданная константа (при рассмотрении на конечном интервале) или T=¥ (при рассмотрении на бесконечном интервале).
, T>t0 заданная константа (при рассмотрении на конечном интервале) или T=¥ (при рассмотрении на бесконечном интервале).
В качестве выхода системы, чтобы избежать больших значений управления, выбран вектор  . Также будет учитываться неопределенность в начальном состоянии системы, задаваемая в виде эллипсоида с матрицей
. Также будет учитываться неопределенность в начальном состоянии системы, задаваемая в виде эллипсоида с матрицей 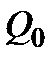 , т.е.
, т.е.
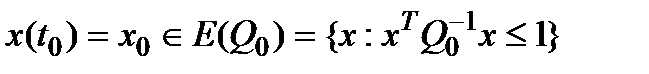 (1.3)
(1.3)
При этом для рассматриваемой системы (1.1) определим матрицы в (1.2)
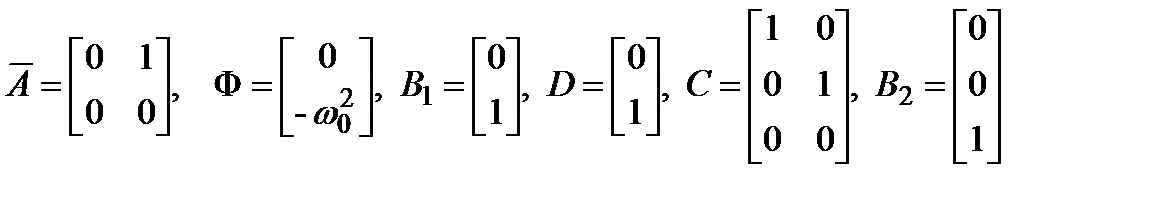 .
.
Линеаризованная система относительно положения равновесия x=0 получается из исходной заменой нелинейности 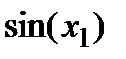 на
на 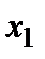 :
:
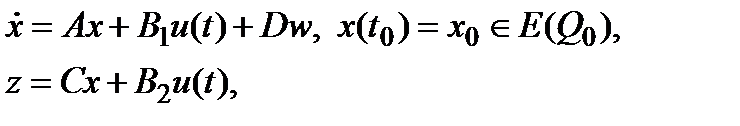 (1.4)
(1.4)
где матрица A определяется как 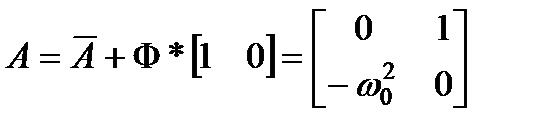 .
.
Предположим, что неопределенные возмущения являются непрерывными функциями, ограниченными в каждый момент времени:
 . (1.5)
. (1.5)
Множество таких функций обозначим как W=Ew(I).
Обозначим G+ - множество 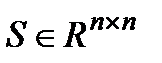 симметрических (S=ST) неотрицательно определенных (S>0) матриц, и G+ - множество
симметрических (S=ST) неотрицательно определенных (S>0) матриц, и G+ - множество 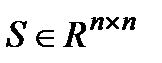 симметрических (S=ST) положительно определенных (S>0) матриц. Известно, что G+ - есть телесный и воспроизводящий конус, с помощью которого вводится частичный порядок в пространстве симметрических матриц
симметрических (S=ST) положительно определенных (S>0) матриц. Известно, что G+ - есть телесный и воспроизводящий конус, с помощью которого вводится частичный порядок в пространстве симметрических матриц 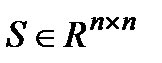 .
.
Задача состоит в синтезе управления в виде обратной связи по состоянию
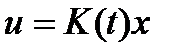 , (1.6)
, (1.6)
стабилизирующего замкнутую систему и подавляющего начальные отклонения и воздействие внешних возмущений в смысле минимальности ограничивающего эллипсоида для выхода z.
Задача синтеза сводится к оптимизации критерия при ограничениях в виде линейных матричных неравенств. В качестве критерия обычно берется след матрицы, определяющей размер инвариантного или ограничивающего выход эллипсоида.
Синтез модального регулятора с заданным расположением собственных значений матрицы замкнутой системы
Задается расположение собственных значений (корней характеристического полинома) p=[-0.8 -3] матрицы A+B*K замкнутой системы. С использованием функции place пакета Matlab производится синтез регулятора u=Kx в форме обратной связи по состоянию
K=[];
p=[-0.8 -3];
K=-place(A,B1,p);
ABK=A+B1*K;
eig(ABK)
В результате получены коэффициенты регулятора
K =[ –2.7500 –4.0000].
При этом матрица замкнутой системы
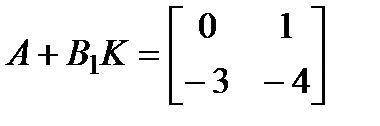
имеет заданные собственные значения [–1.0000 –3.0000]. Следовательно, линеаризованная система, замкнутая с модальным регулятором асимптотически устойчива.
