Свойства определенного интеграла
Определенный интеграл обладает 3, 4 свойствами неопределенного и еще таким свойством:
Если поменять местами пределы интегрирования, то знак перед интегралом изменится на противоположный.
Вычисление определенного интеграла.
Определенный интеграл вычисляется по формуле Ньютона-Лейбница.
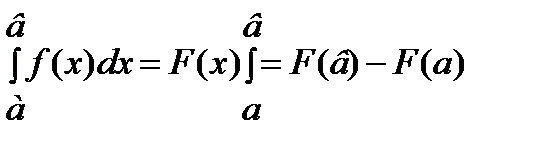
Пример: 
Решить в аудитории
1) 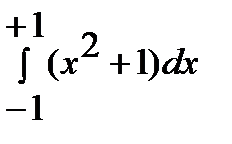 ответ
ответ 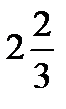
2)  ответ 3,25
ответ 3,25
3) 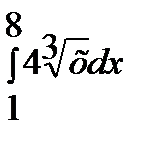 ответ 45
ответ 45
4)  ответ
ответ 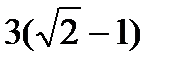
5)  ответ 47
ответ 47
6) 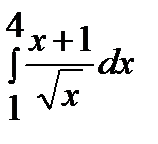 ответ
ответ 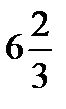
7)  ответ 2
ответ 2
8)  ответ 3,96
ответ 3,96
9)  ответ
ответ 
Домашнее задание
Вычислить интегралы
1.  ответ
ответ 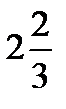
2. 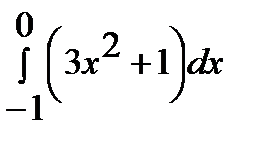 ответ 2
ответ 2
3. 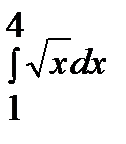 ответ
ответ 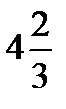
4.  ответ
ответ 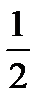
5.  ответ 1
ответ 1
6.  ответ 2
ответ 2
7.  ответ 2
ответ 2
8.  ответ ≈-0,68
ответ ≈-0,68
Урок № 74 Тема 8.5.: Применение определенного интеграла для вычисления площадей плоских фигур.
План.
Определение определнного интеграла.
Решение упражнений.
Определение. Определенный интеграл  численно равен площади фигуры, заключенной между осью ох, графиком функции у=f(x) и прямой х=а; х=в.
численно равен площади фигуры, заключенной между осью ох, графиком функции у=f(x) и прямой х=а; х=в.
Решить
1. Вычислить S фигуры ограниченной кубической параболой у=х3, осью ох и прямыми х=-1; х=1. Ответ 0,5 кв.ед.
2. Вычислить S фигуры, ограниченной кривой y=х2-4х и осью ох. Ответ  ед.пл.
ед.пл.
3. Вычислить S фигуры, ограниченной графиком функции y=cosx, осью ох и прямой 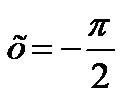 и
и  . Ответ 20 кв.ед.
. Ответ 20 кв.ед.
4. Вычислить S фигуры, ограниченной линиями у=х+3, у=х2+1. Ответ 4,5 ед.пл.
Домашнее задание
1. Определить S фигуры, ограниченной прямой у=5х осью ох, прямой х=3. Ответ 22,5 ед.пл.
2. Определить S фигуры, ограниченной кривой  осью ох и прямыми х=2; х=4. Ответ
осью ох и прямыми х=2; х=4. Ответ  ед.пл.
ед.пл.
3. Определить S фигуры, ограниченной осью ох и линией у=2х-х2. Ответ  ед.пл.
ед.пл.
4. Определить S фигуры, ограниченной линиями 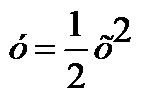 и у=4-х. Ответ 18 ед.пл.
и у=4-х. Ответ 18 ед.пл.
Урок №75 .Тема 9.1. : Многогранники. Призма. S бок. призмы. S полн. призмы.
План занятия.
1.Определение многогранника.
2. определение призмы. Виды призм.
3. Площадь боковой и полной поверхности призмы.
Определение:
Объединение ограниченной пространственной области и ее границы называют телом.
Границу тела называют его поверхностью, а пространственную область -внутренней областью.
Многогранником называют тело, поверхность которого есть объединение конечного числа многоугольников.
Многоугольники, составляющие поверхность многогранника называют его гранями, стороны этих многоугольников -ребрами, а вершины- вершинами.
Отрезок, который соединяет две вершины многогранника, не принадлежащие одной грани, называют диагональю многогранника.
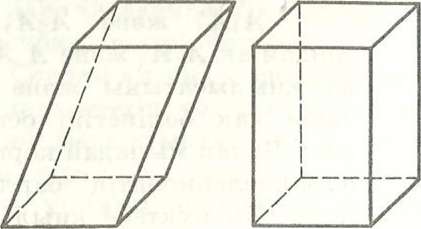
Определение: Призмой называется многогранник, две грани которого –одноименные многоугольники, лежащие в параллельных плоскостях, и любые два ребра, не лежащие в этих плоскостях, параллельны.
Различают прямые и наклонные призмы. Призма, боковые ребра которой перпендикулярны плоскости основания, называется прямой призмой. Если боковые ребра не перпендикулярны плоскостям оснований, то ее называют наклонной призмой.