Дискретная случайная величина

Случайная величина X называется дискретной, если множество всевозможных значений (x₁, x₂, … x_n) счетное. Случайная величина полностью задается своим рядом распределения, т.е. парами (x_i, p_i, i = 1,2,…n).

! Пример: Ряд распределения случайной величины (выпавшее очко) при бросании игральной кости имеет вид:

X
P	1/6	1/6	1/6	1/6	1/6	1/6

Сумма вероятностей всевозможных значений случайной величины равна 1:

S p_i = 1.

Соотношение между возможными значениями случайной величины и соответствующими вероятностями называется законом распределения дискретной случайной величины.

Известные типы распределения дискретных случайных величин – это биномиальный, пуассоновский и геометрический законы распределения.

Случайная величина X называется распределенной по биномиальному закону с параметрами n, p > 0, если X может принимать лишь конечное счетное число значений 0, 1, 2, …, n с вероятностью 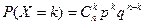(формула Бернулли), где q = 1 – p.

Рассмотрим какое-нибудь событие (например, появление герба при подбрасывании монеты), которое происходит с вероятностью p. Проведем серию n опытов в одинаковых условиях. Событие X – это появление герба в k раз (k = 0, 1, … n). Вероятность события X подсчитывается по формуле Бернулли.

@ Задача 1: Найти закон распределении появления герба, при подбрасывания монеты в 5 раз.

Решение: Случайная величина появления герба принимает 6 значений: 0, 1, 2, 3, 4, 5 с рядом распределением (p = ½; q = ½ ):

X
P	1/32	5/32	10/32	10/32	5/32	1/32

@ Задача 2: Некоторый стрелок попадает в цель с вероятностью 0,6. Он собирается произвести 10 выстрелов. Найти вероятность того, что он попадет в цель: а) 3 раза; б) хотя бы один раз.

Решение: Условия проведения опыта соответствуют схеме Бернулли, с p = 0,6; q = 1 – p = 0,4; n = 10.

а) Следовательно, ;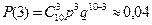

б) » 1.

Случайная величина X называется распределенной по закону Пуассона с параметром а > 0, если X может принимать бесконечное счетное число значений 0, 1, 2, …, n, … с вероятностью .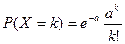

При n ® ¥и p ® 0биномиальный закон приближается к закону распределения Пуассона, где a = np.

Случайная величина X называется распределенной по закону геометрической прогрессии с параметром p > 0, если X может принимать бесконечное счетное число значений 1, 2, …, n, … с вероятностью 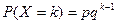, где p – вероятность наступления события A, q = 1 – p – вероятность не наступления события A.

Рассмотрим какое-нибудь событие (выбор автомобиля), которое происходит с вероятностью p. Проведем серию опытов в одинаковых условиях до тех пор, пока не случится это событие (будет выбран автомобиль). Это число опытов, включая последний – «успешный», и принимает событие X в качестве своего значения (число отвергнутых автомобилей)