Анализ временных рядов

Графики нагрузки в ЭЭС являются последовательностями наблюдений или расчетных значений, показывающих изменения мощности в течение определенного периода времени. В суточных, недельных и годовых графиках отображается периодичность процесса изменения мощности нагрузки, связанная с режимом работы людей, сменой дня и ночи, недельными циклами и сезонными изменениями в течение года.

Суточные графики дней недели в общем повторяются изо дня в день с небольшими случайными различиями и режимами выходных и праздничных дней. Средний рост или снижение нагрузки в течение недели или нескольких недель связан с сезонными изменениями, в особенности в осенний и весенний периоды. Такие изменения, происходящие в среднем, относят к трендовым (непериодическим) составляющим графика нагрузки. Эти изменения для годовых графиков обусловлены естественным ростом нагрузки потребителей.

Суточные, недельные и годовые графики нагрузки часто прогнози-руют посредством разделения их на трендовую, периодическую и случайную составляющие:

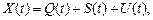(5.58)

где Q(t) – тренд – устойчивые систематические изменения;

S(t) – периодическая составляющая – колебания относительно тренда;

U(t) – нерегулярная составляющая – случайный шум.

Подобный подход справедлив, если принять гипотезу о том, что резких изменений во временном ряду не произойдет.

Пусть имеется временной ряд значений месячных максимумов мощности нагрузки за несколько лет (рис. 5.21).

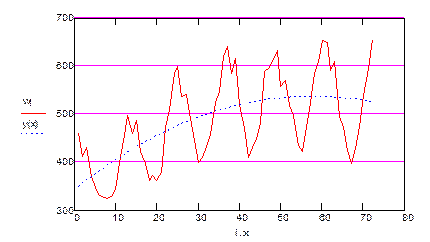
Рис. 5.21. Ретроспектива временного ряда

Для выделения трендовой составляющей часто используют полиномиальную модель до третьего порядка включительно:

(5.59)

Иногда при выделении тренда предварительно применяют процедуру сглаживания, которая устраняет периодическую и случайную составляющие.

После вычитания из X(t) трендовой составляющей получается временной ряд, имеющий периодическую составляющую, которая вызвана суточными, недельными и сезонными периодами.

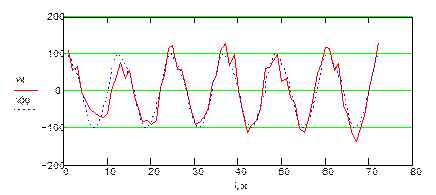
Рис. 5.22. Временной ряд без трендовой составляющей

Если имеется N результатов наблюдений за период T (N = 12 в годовом цикле, N = 7 – в недельном и N = 24 – в суточном), то периодическая модель процесса может быть представлена рядом Фурье

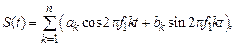(5.60)

где n – количество частот, включенных в модель.

В общем случае наивысшая частота гармонического разложения дискретного ряда, называемая частотой Найквиста, определяется половиной интервала между наблюдениями, например при N = 12, n = 24.

– основная частота гармонического ряда.

Дисперсия, учитываемая i-й гармоникой:

(5.61)

Суммарная дисперсия . Как правило, первые три гармоники описывают до 90 % всей дисперсии.

Случайная составляющая

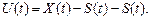(5.62)

Для U(t) определяются статистические характеристики. Прогноз случайной составляющей ведется по одной из моделей прогноза случайного процесса. Сразу следует оценить интервал корреляции, и если прогноз ведется на время упреждения больше, чем интервал корреляции, то фактически по случайной составляющей оценивается лишь ошибка прогноза, так как после вычитания регулярных составляющих математическое ожидание процесса равно нулю.

Оценка коэффициентов моделей регулярных составляющих

Тренд

Оценка коэффициентов полиномиальной модели тренда может быть сделана разными способами:

1) с помощью функций Mathcad c := regress(k,P,m) и Q_m(t) := in-terp(c,k,P,t). Здесь c – вектор коэффициентов, используемый функцией interp; k – вектор дискретных моментов времени, для которых заданы значения ретроспективы; P – вектор значений ретроспективы; m – порядок полинома (как 0, 1, 2 или 3); t – аргумент функции тренда. Можно также записать Q_m(t) = interp(regress(k,P,m), k,P,t);

2) как решение системы линейных уравнений по методу наименьших квадратов A = (V^TV)^–1V^TP. Функция тренда: . Здесь V – матрица, первый столбец которой состоит из единиц, второй – вектор k, третий вектор из элементов k в квадрате и т. д. V_i,j =
= k_ij–1 ( i = 1…n, j = 1… m + 1), где n – количество данных ретроспективы.

Экспоненциальная модель тренда может быть получена с помощью функции expfit(k,P,vg), которая возвращает вектор коэффициентов модели . Здесь вектор vg – начальные приближения для искомых коэффициентов модели.

Периодическая составляющая

Коэффициенты полигармонической составляющей процесса являются коэффициентами гармонического полинома вида (5.60). Вектор коэффициентов модели получается как решение системы линейных уравнений B = (V^TV) ^–1V^TW. Здесь V – матрица из n строк и 2m столбцов; n – количество данных ретроспективы; m – количество частот, включенных в модель. Каждая последовательная пара столбцов матрицы V соответствует одной частоте и состоит из коэффициентов, вычисляемых как функции косинуса и синуса из выражения (5.60):

(5.63)

W – вектор, полученный из P вычитанием трендовой составляющей.

Возможно моделирование периодической составляющей с помощью другого представления ряда Фурье:

, (5.64)

где искомыми параметрами являются .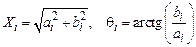

Пример.Чтение данных из файла Retro.prn

Представим тренд постоянной функцией, равной среднему значению за 5 суток

544.5

545.5

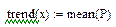
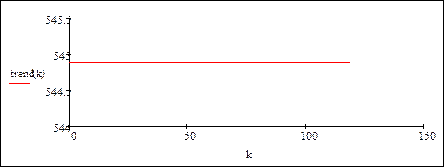
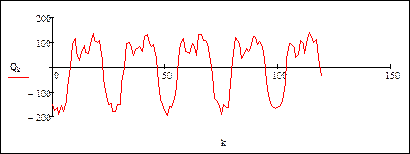
Остаточный временной ряд без тренда

–200

–100

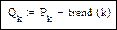
Моделирование периодической составляющей – 6 гармоник:

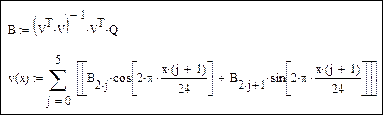
Графическое изображение периодической составляющей:

–100

–200

Остаточный временной ряд без тренда и периодической составляющей – случайная составляющая:

–20

–40

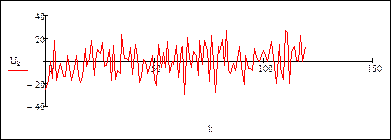
Определение статистических характеристик случайной составляющей временного ряда: среднее значение, медиана, среднеквадратическое отклонение:

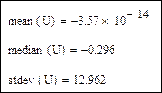
Прогнозируемый график есть сумма тренда и случайной составляющей:

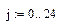
За ошибку прогноза принимаем среднеквадратическое отклонение случайной составляющей временного ряда:

Вопросы для самопроверки

1. Как подразделяются детерминированные физические процессы?

2. Как подразделяются случайные физические процессы?

3. Что такое прогноз?

4. Какие два вида переменных, зависящих от времени, выделяют при прогнозировании?

5. Как подразделяют прогноз по времени упреждения?

6. Дайте определение экспоненциальной модели прогнозирования.

7. В чем принципиальное различие логистической и экспоненциальной моделей прогнозирования?

8. Какие основные методы используют для прогнозирования случайных процессов?

9. Какие факторы влияют на прогноз суточных графиков нагрузки электроэнергетической системы?

10. В чем заключается прогноз графиков нагрузки методом анализа временных рядов?