Временные и частотные характеристики звеньев второго порядка
ПФ звена второго порядка можно представить в нескольких формах за-писи:
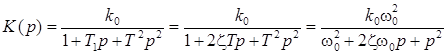 , (2.5)
, (2.5)


| |
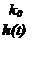 где z– коэффициент демпфирования. Возможно представление ПФ в виде
где z– коэффициент демпфирования. Возможно представление ПФ в виде | |

 . (2.6)
. (2.6) 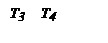



| |
| |

|
 Форма (2.6) удобна исключительно для апериодических звеньев.
Форма (2.6) удобна исключительно для апериодических звеньев. Свойства апериодического и колебательного позиционных звеньев отличаются прежде всего разными значениями величин z.
Для апериодических звеньев второго порядка z ³ 1. Дляних характерна монотонная форма ПХ и плавная, без подъемов, АЧХ (ЛАЧХ), имеющая в области высоких частот крутизну спада 40 дБ/декаду (прил. 2).
ПХ такого звена определяется по формуле (прил. 1)
 , (2.7)
, (2.7)
а ИХ – как
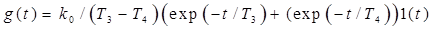 . (2.8)
. (2.8)
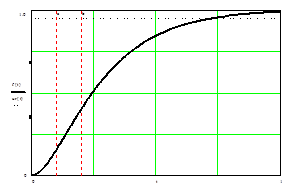
График ПХ h(t) (рис. 2.3) дает представление об определении параметров ПФ по экспериментальной характеристике.
(См. также рис. 2.4 и 2.5, график 4.)
Если в (2.6) – (2.8) Т3 = Т4 (z = 1 или Т1 = 2Т2 в (2.5)), то
 ,
,  . (2.9)
. (2.9)
При Т4 ® 0 звено вырождается в апериодическое звено первого порядка.
 У колебательного звенаz < 1.
У колебательного звенаz < 1.
Если параметр демпфирования z лежит в пределах  , то на ПХ (рис. 2.4, график 3) появляется выброс (зона перерегулирования), хотя АЧХ (рис. 2.5) по существу не меняется.
, то на ПХ (рис. 2.4, график 3) появляется выброс (зона перерегулирования), хотя АЧХ (рис. 2.5) по существу не меняется.
 По мере уменьшения z ярче проявляются резонансные свойства звена (рис. 2.5, графики 1 и 2), и соответственно увеличивается колебательность временных характеристик (число пересечений уровня h(¥) (рис. 2.4, графики 1 и 2) и g(¥).
По мере уменьшения z ярче проявляются резонансные свойства звена (рис. 2.5, графики 1 и 2), и соответственно увеличивается колебательность временных характеристик (число пересечений уровня h(¥) (рис. 2.4, графики 1 и 2) и g(¥).
Хотя при увеличении z уменьшается время запаздывания (ТЗ1 – ТЗ4 на рис. 2.4) и увеличивается максимальная скорость нарастания ПХ  , время регулирования из-за усиления колебательности процесса может даже увеличиться (на рис. 2.4
, время регулирования из-за усиления колебательности процесса может даже увеличиться (на рис. 2.4
ТР1 > ТР2 > ТР3 < ТР4 ).
Число полных периодов колебаний N за время регулирования (N = 1 на ПХ рис. 2.6, N = 2 на ПХ рис. 2.4, график 1).
Временные характеристики колебательного звена описываются выражением
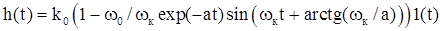 =
=
= 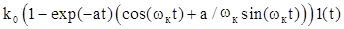 , (2.10)
, (2.10)
 . (2.11)
. (2.11)
В (2.10) – (2.11) 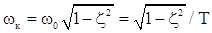 – собственная частота колебаний звена;
– собственная частота колебаний звена;  – коэффициент затухания; также a и wкявляются соответственно действительной и мнимой частями корней характеристического уравнения звена (
– коэффициент затухания; также a и wкявляются соответственно действительной и мнимой частями корней характеристического уравнения звена (  ):
):
 . (2.12)
. (2.12)
 Графики звена второго порядка с колебательной ПХ изображены на рисунках 2.4 и 2.6.
Графики звена второго порядка с колебательной ПХ изображены на рисунках 2.4 и 2.6.
График на рисунке 2.6 иллюстрирует, как по экспериментальной ПХ реального звена можно найти параметры соответствующего колебательного звена.
Если параметр демпфирования z лежит в пределах  , то АЧХ по существу не меняется (рис. 2.5) по сравнению с апериодическим звеном (z ³ 1), хотя на ПХ (рис. 2.4, график 3) появляется выброс.
, то АЧХ по существу не меняется (рис. 2.5) по сравнению с апериодическим звеном (z ³ 1), хотя на ПХ (рис. 2.4, график 3) появляется выброс.
 Только в случае
Только в случае  наблюдается заметный подъем АЧХ в некотором диапазоне частот, при этом показатель колебательности М и «резонансный горб» увеличиваются с уменьшением z. Обычно резонансная частота w0 несколько ниже wк, но приближается к ней с ростом z
наблюдается заметный подъем АЧХ в некотором диапазоне частот, при этом показатель колебательности М и «резонансный горб» увеличиваются с уменьшением z. Обычно резонансная частота w0 несколько ниже wк, но приближается к ней с ростом z
(рис. 2.5).
На рисунке 2.7 приведены примеры нормированных АЧХ звеньев второго порядка: апериодического (график 1) и колебательного (график 2).
