Случайная величина, зависящая отмножества независимых недоминирующих факторов подчиняется закону гаусса

Причем, если найти вероятность попадания в интервале 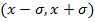, то эта величина будет постоянная для любого нормального распределения и равна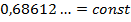

Примеры. 1. Подсчитаем среднее отклонение числа молекул в одном моле газа при нормальных условиях, то есть атмосферное давление и объеме . Это будет около молекул! Несмотря на то, что число огромно, относительно общего числа молекул это будет совсем незначительно: .

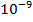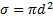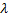2. Ранее мы искали длину свободного пробега молекулы газа при помощи динамического метода. Теперь покажем, насколько проще выкладки, если пользоваться статистическим методом: столкновение обязательно произойдёт, если в объёме . Будет не более одной молекулы ,

Тогда вероятность:

3.3 Статистические распределения для идеального газа. Координата и скорость молекулы как случайные величины. Фазовое пространство координат и импульсов, обобщенные координаты. Функция Гамильтона. Каноническое распределение Гиббса. Распределение молекул по скоростям Масквелла. Закон распределения энергии по степеням свободы. ТДС в поле внешних сил. Идеальный газ в гравитационном поле, распределение Максвелла-Больцмана.

Простейшее фазовое пространство представляется как пространство координат и импульсов – 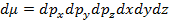. Намного более сложной является задача о том, чтобы подсчитать зависимость не от скоростей и положения молекул в пространстве, а от того, какой энергией они обладают.

Пусть нам даны 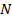частиц и они взаимодействуют только в момент столкновения, эти частица находятся в некотором внешнем силовом поле. Необходимо найти наиболее вероятное (а следовательно, и равновесное) распределение этих элементов по энергии .

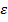Представим, что эта система – идеальный газ. Тогда из свойств этой математической модели следует, что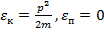

Но поскольку имеется внешнее силовое поле, то также речь идет и о потенциальной энергии внешнего силового поля:

Но вспомним, что сейчас речь шла об идеальном газе – по сути, математической модели. Если же в качестве системы взять реальный газ, например, воздух, то тогда у молекул есть диаметр, возможно вращательное и колебательное движение, потому в фазовое пространство будут добавляться все новые и новые координаты, что неумолимо приведет к перегруженности каких бы то ни было расчетов. Поэтому вводится понятие обобщенных координат –водится по координате на кинетическую и на потенциальную составляющие энергии как координаты в фазовом пространстве:

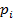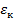– обобщенная координата, отвечающая за ; - обобщенная координата, отвечающая за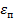

Полная энергия в таком случае будет искаться по формуле: 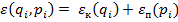В этом фазовом пространстве каждая точка будет являться энергетическим состоянием одной молекулы. Тогда

Тогда 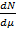– плотность распределения, где 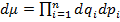, также можно написать: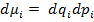

Разумеется, есть естественное желание свести плотность к знакомой нам формуле: – и сделать функцию плотности распределения по энергии.

Теорема Лиувилля: если функция распределения в фазовом пространстве является функцией обобщенных координат (а она является), то она зависит только от значений энергии, а не от конкретного значения этих обобщенных координат.Координаты являются функциями времени.

В математическом смысле это означает, что:

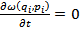Иначе говоря: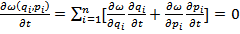

Аксиома Гиббса: Если плотность распределения вероятности в фазовом пространстве есть функция обобщенных координат не иначе как через функцию Гамильтона, то тогда:

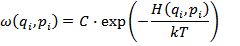, где – Гамильтониан. Это каноническое распределение Гибсса.

Свойства распределения Гиббса:

-нет ограничения на обмен энергии;

-функция Гамильтона – случайная величина;

-если ТДС может быть представлена в виде двух подсистем: так, что гамильтониан системы равен сумме гамильтонианов подсистем ,то есть , то , то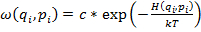гда систему можно разбить на две подсистемы и рассматривать их в отдельност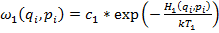и: и .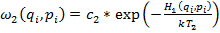

Таким образом, основная задача статистического метода по Гибссу сводится к нахождению функций Гамильтона для различных термодинамических систем.

Рассмотрим подробнее эту задачу для простейших ТДС. Функция Гамильтона (по определению) это функция обобщённых координат, удовлетворяющая уравнениям:

Перейдем теперь к переменным Ньютона: 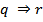– радиус; 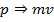– импульс. ТДС - идеальный газ в поле сил земного тяготения.

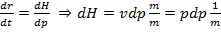, тогда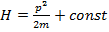

По второму закону Ньютона (так как – гравитационная сила) 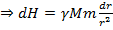(минус ушел, так как направления противоположны)

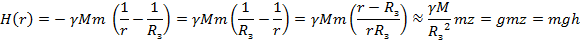
Таким образом, ,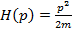

Тогда функция распределения будет выглядеть:

– распределение Максвелла-Больцмана

Найдем условие равновесия системы c гамильтонианом , состоящую из двух вышеуказанных подсистем.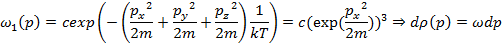

Воспользуемся условием нормировки для нахождение Сonst .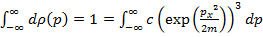

Отсю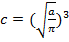да Тогда . Разобьем на подсистемы по проекциями скорости молекул на координатные оси:

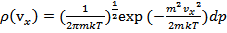. Это распределение Гаусса при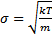

=

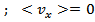
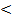
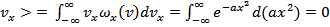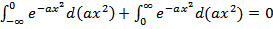
Закон распределения энергии по степеням свободы

Рассмотрим распределение Гаусса:

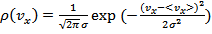. Максимальная вероятность приходится на значение

Тогда

Таким образом, на одну степень свободы приходится энергия, равная:

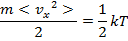
Это легко проверить: ведь такая энергия приходится на одну координату, следовательно, на три координаты будет 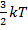, что верно для идеального газа.

Таким образом,равновесное состояние системы (по энергии) соответствует равномерному распределению энергии по всем степеням свободы.

Напомним, что равновесное состояние по координатам соответствует равномерному распределению по объёму.

Получим классическое распределение молекул по скорости Максвелла. Элемент объёма в пространстве скоростей , и 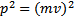. Получим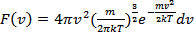

Это распределение Максвелла по модулям скоростей молекул.

Получим распределение Больцмана молекул атмосферы Земли

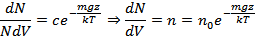
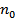– концентрация молекул около поверхности Земли

Если умножить обе части на 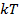, то получим соотношения для давления - барометрическую формулу:

Обобщение Больцмана. Если ТДС находится во внешнем силовом поле, в котором энергия элементов системы

то распределение элементов по по концентрации (плотности) имеет вид:

Раздел 4. Элементы статистической термодинамики

4.1 Основные положения статистической термодинамики. Условия равновесия. Начала термодинамики.

В данном разделе речь пойдет о термодинамических системах, причем под «термодинамикой» на этот раз понимаются действительно процессы, связанные с теплотой и передачей тепла. Будут рассматриваться новые системы, в которых, в отличие от рассматриваемых ранее, возможен обмен частицами.

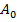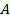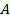Нулевое начало. Если ТДС находится в равновесном состоянии с системами и , то тогда система находится в равновесном состоянии с системой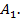

Это интуитивно понятно и, более того, может быть подкреплено чисто математическими выкладками:

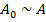тогда

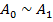
Также данное начало можно объяснить при помощи статистической физики:

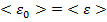тогда

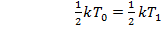
Системы стремятся к равновесному состоянию, если 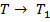(это еще необходимо показать, но опять же интуитивно понятно)

Первое начало. Закон сохранения энергии. Рассмотрим всю энергию системы (обозначим ее как )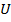

В самом общем случае она может складываться из множества компонент:

Для простых ТДС можно ограничиться первыми двумя слагаемыми:

Возьмем идеальный газ. Тогда состояние этой системы подчиняется уравнению Менделеева - Клапейрона: 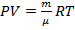. Возьмем один моль вещества, то есть 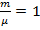. Тогда:

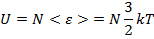
пропорциональна температуре 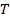. Отсюда верно следующее: . При условии, что N=Const.

Из уравнения Менделеева - Клапейрона получаем: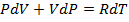

Первое слагаемое есть некоторая работа, второе – некоторое количество тепла.

Количество тепла – это изменение внутренней энергии термодинамической системы без совершения работы (чтобы исключить работу, необходимо, чтобы )

Таким образом, первое начало термодинамики будет выглядеть следующим образом:

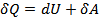Или:

В ТДС, в которых происходит не только обмен тепловой энергий, но происходит изменение количество вещества (химические реакции) первое начало примет вид:

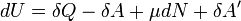
Изменение полной энергии системы в квазистатическом процессе равно количеству теплоты , сообщённому системе, в сумме с изменением энергии, связанной с количеством вещества 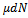при химическом потенциале , и работы совершённой над системой внешними силами и полями, за вычетом работы , совершённой самой системой против внешних сил.

Второе начало(оно служит именно для того, чтобы предугадать направление изменения состояния системы). Например, это начало накладывает ограничения на направление термодинамических процессов, запрещая самопроизвольную передачу тепла от менее нагретых тел к более нагретым.

В классической физике было множество формулировок второго начала в различных областях, в том числе и утверждение о том, что вечный двигатель невозможен. Невозможен циклический процесс (двигатель), единственным результатом которого является превращение тепла в работу. Т.е. в циклическом процессе часть энергии теряется, (не превращается в работу).

С точки зрения статистической физики второе начало термодинамики имеет статистический характер: оно справедливо для наиболее вероятного поведения системы. Существование флуктуаций препятствует точному его выполнению, однако вероятность сколь-нибудь значительного нарушения крайне мала.

Третье начало термодинамики относится только к равновесным состояниям.

Поскольку на основе второго начала термодинамики энтропию можно определить только с точностью до произвольной аддитивной постоянной (то есть, определяется не сама энтропия, а только её изменение).

Tретье начало термодинамики может быть использовано для точного определения энтропии. При этом энтропию равновесной системы при абсолютном нуле температуры считают равной нулю.

4.2 Термодинамические процессы. Превращение тепла в работу. Циклические процессы. Энтропия и энергия. «Энтропийная» формулировка второго начала термодинамики. Энтропия и вероятность, статистический смысл энтропии.. Информационный смысл энтропии. Парадокс Максвелла

В начале 19-го века перед учеными встал вопрос о том, можно ли создать идеальный термодинамический цикл, чей КПД был бы максимальным. Такой цикл был найден военным инженером Сади Карно.

Описание цикла Карно:

1. Изотермическое расширение. В начале процесса рабочее тело имеет температуру T_H, то есть температуру нагревателя. Затем тело приводится в контакт с нагревателем, который изотермически (при постоянной температуре) передаёт ему количество теплоты Q_H. При этом объём рабочего тела увеличивается.

2. Адиабатическое (изоэнтропическое) расширение. Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.

3. Изотермическое сжатие. Рабочее тело, имеющее к тому времени температуру T_X, приводится в контакт с холодильником и начинает изотермически сжиматься, отдавая холодильнику количество теплоты Q_X.

4. Адиабатическое (изоэнтропическое) сжатие. Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.

Несмотря на то, что Карно в свое время лишь постулировал то, что КПД данного цикла будет максимальным, дальнейшие исследования показали, что это действительно так, причем:

Для любых других циклов значение величины 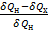оказалось меньше, чем для цикла Карно.

Исследуем цикл Карно.

Отсюда следует, что 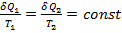для цикла Карно.

Энтропия – это функция параметров состояния , дифференциал которой равен 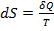– то есть получаемой системой приведённой теплоте.

Для цикла Карно dS = 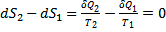Для реальных процессов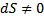

Вообще говоря, 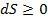в изолированной системе, поскольку абсолютная температура всегда больше нуля.

Отсюда Больцман сделал вывод о «тепловой смерти Вселенной».

Попытаемся расшифровать второе начало термодинамики с помощью статистической термодинамики. Попытаемся ввести некоторый параметр, указывающий направление движения системы к равновесному состоянию.

Пусть система 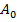находится в равновесном состоянии с энергией 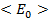. Обозначим – число состояний, соответствующих равновесному состоянию системы.

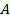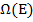Разобьем эту систему на две: и , им будут соответствовать равновесные состоянии с энергией и < >, и число состояний и 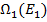соответственно.

При этом Гамильтониан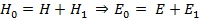

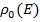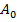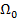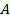Найдем вероятность того, что система из всех состояний находится в состоянии , когда система имеет энергию 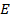. По определению вероятности:

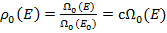– эта величина отличается от 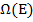тем, что она может быть скомбинирована с любыми другими состояниями системы. Тогда

Воспользуемся распределение Гиббса: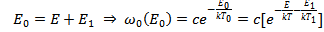

Запишем вероятность состояния системы A₀ c энергией в интервале E, E+dE через функцию распределения:

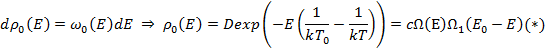
Условием для равновесия является максимум вероятности: 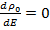. Заметим, что производная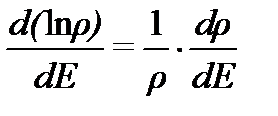

Логарифмируя 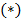, получаем:

Так как 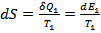, то:

Таким образом, получили формулу энтропии (самой энтропии, а не ее дифференциала).

Рассмотрим энтропию как меру неопределенности. С учётом третьего начала. При 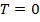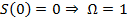, то есть при абсолютном нуле у системы может быть лишь одно состояние, нет никакой неопределенности. Если же энтропия растет, то число состояний увеличивается и, следовательно, система становится более неопределенной.

Что касается информационной составляющей энтропии, то было предложено видоизменить ее формулу следующим образом: 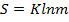, если 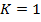, то информация измеряется в натах, если же 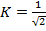, то в битах, если же 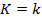(то есть постоянной Больцмана), то в физических единицах.

Таким образом, в энтропии скрыты энергетическая и информационная составляющие.

Парадокс Максвелла: Пусть имеем сосуд с газом, разделённый непроницаемой перегородкой на две части: правую и левую. В перегородке отверстие с устройством (так называемый демон Максвелла), которое позволяет пролетать быстрым (горячим) молекулам газа только из левой части сосуда в правую, а медленным (холодным) молекулам — только из правой части сосуда в левую. Тогда через большой промежуток времени, "горячие" (быстрые) молекулы окажутся в правом сосуде, а "холодные" — "останутся" в левом. Таким образом получается, что демон Максвелла позволяет нагреть правую часть сосуда и охладить левую без дополнительного подвода энергии к системе. Энтропия для системы, состоящей из правой и левой части сосуда, в начальном состоянии больше, чем в конечном, что противоречит термодинамическому принципу «неубывания» энтропии в замкнутых системах. Парадокс разрешается, если рассмотреть замкнутую систему, включающую в себя демона Максвелла и сосуд. Для функционирования демона Максвелла необходима передача ему энергии от стороннего источника. За счёт этой энергии демон получает информацию о энергетическом состоянии молекулы и производит разделение горячих и холодных молекул в сосуде, то есть переход в состояние с меньшей энтропией. В этом случае суммарная энтропия не убывает.