Построение математической модели
Страницы сам изменишь :)
Введение
Динамическое программирование (динамическое планирование) – это раздел математического программирования, который изучает совокупность приёмов и методов, позволяющих находить оптимальные решения, основанные на вычислении последствий каждого решения и выработке оптимальной стратегии для последующих решений.
Задачи динамического программирования являются многоэтапными, поэтому термин «динамическое программирование» не столько определяет особый тип задач, сколько характеризует методы нахождения решения отдельных классов задач математического программирования.
В общем случае задача динамического программирования формулируется следующим образом. Например данная физическая система 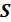 находится в некотором начальном состоянии
находится в некотором начальном состоянии 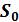 и является управляемой. Благодаря осуществлению некоторого управления (некоторой операции)
и является управляемой. Благодаря осуществлению некоторого управления (некоторой операции) 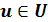 указанная система переходит из начального состояния
указанная система переходит из начального состояния 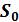 в конечное состояние
в конечное состояние 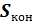 . При этом качество каждого из реализуемых управлений
. При этом качество каждого из реализуемых управлений 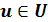 характеризуется соответствующим значением функции
характеризуется соответствующим значением функции 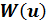 . Задача состоит в том, чтобы из множества возможных управлений
. Задача состоит в том, чтобы из множества возможных управлений
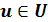 найти такое
найти такое 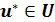 , при котором функция
, при котором функция 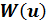 принимает экстремальное значение
принимает экстремальное значение 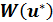 .
.
Можно выделить два класса задач, к которым методы динамического программирования применяются наиболее удачно.
Первый класс – это задачи планирования деятельности экономического объекта (предприятия, отрасли и т.п.) с учётом изменения потребности в производимой продукции во времени.
Второй класс задач – задачи оптимального распределения ресурсов между различными направлениями во времени.
Наибольшей эффективности методы динамического программирования достигают там, где по самому существу задачи приходится принимать решения по этапам.
Рассмотрим основные теоретические аспекты решения задач методом динамического программирования.
Будем считать, что состояние рассматриваемой системы 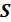 на
на 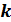 – ом шаге
– ом шаге
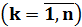
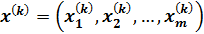 (1)
(1)
которые получены в результате реализации управления 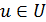 обеспечивающего переход системы
обеспечивающего переход системы 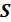 из состояния
из состояния 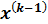 в состояние
в состояние 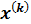 .
.
Далее, будем считать, что если в результате реализации –го шага обеспечен определённый доход, также зависящий от исходного состояния системы 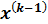 и выбранного управления
и выбранного управления 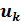 , равный
, равный 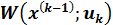 , то общий доход за
, то общий доход за 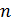 шагов составляет
шагов составляет
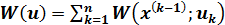 (2)
(2)
где 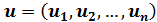 .
.
Таким образом, сформулированы два условия, которым должна удовлетворять рассматриваемая задача динамического программирования. Первое условие обычно называют условием отсутствия последействий, а второе – условием аддитивности целевой функции задачи оптимизации.
Задача оптимизации в этом случае состоит в отыскании оптимальной стратегии управления, т.е. такой совокупности управлений
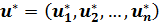 (3)
(3)
в результате реализации которых система 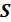 за
за 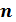 шагов переходит из начального состояния
шагов переходит из начального состояния 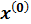 в конечное
в конечное 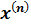 и при этом функция дохода
и при этом функция дохода 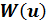 принимает наибольшее значение.
принимает наибольшее значение.
Распределение капитальных вложений – это нелинейная задача распределения ресурсов между предприятиями одного производственного объединения или отрасли.
Предположим, что указано n-пунктов, где требуется построить предприятия одной отрасли, для чего выделена определенная сумма. При этом известен прирост мощности или прибыли для каждого предприятия, в зависимости от суммы капитальных вложений в это предприятие.
Если требуется найти распределение капитальных вложений между предприятиями, то задача состоит в том, чтобы найти такие значения  , при которых значение суммарного прироста прибыли или мощности всей отрасли
, при которых значение суммарного прироста прибыли или мощности всей отрасли
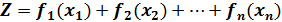 (4)
(4)
было бы наибольшим при ограничениях общей суммы 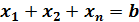 ,
,
где 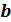 – общая сумма капитальных вложений.
– общая сумма капитальных вложений.
Данная задача решается методом динамического программирования. Для этого необходимо ввести параметр состояния 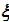 и функцию состояния
и функцию состояния 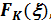
где 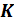 – некоторое количество предприятий, для которых определяется параметр и функция состояния.
– некоторое количество предприятий, для которых определяется параметр и функция состояния.
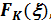 – максимальный прирост прибыли или мощности на первых –предприятиях, если они вместе получат
– максимальный прирост прибыли или мощности на первых –предприятиях, если они вместе получат 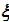 - капитальных вложений.
- капитальных вложений.
Если 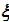 - количество единиц ресурса, то -ое предприятие получит
- количество единиц ресурса, то -ое предприятие получит 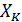 единиц ресурса, то остаток
единиц ресурса, то остаток 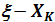 необходимо распределить между предприятиями от
необходимо распределить между предприятиями от 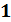 -го до
-го до 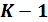 -го так, чтобы был получен максимальный прирост прибыли или мощности
-го так, чтобы был получен максимальный прирост прибыли или мощности 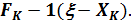 Следовательно, прирост прибыли будет равен
Следовательно, прирост прибыли будет равен 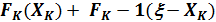 и нужно выбрать такое значение
и нужно выбрать такое значение 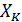 -ое между 0 и x, чтобы увеличение прибыли
-ое между 0 и x, чтобы увеличение прибыли 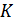 -предприятий было максимальным.
-предприятий было максимальным.
Построение математической модели
Общая сумма в 4 млн. руб. распределяется между пятью предприятиями в количествах, кратных 1 млн. руб. В результате выделение средств -му предприятию в размере 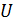 оно дает доход
оно дает доход 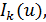
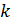 =1,2,3,4,5 величина которого может быть найдена из таблицы №1:
=1,2,3,4,5 величина которого может быть найдена из таблицы №1:
Таблица №1
«Исходные данные»
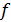 | |||||
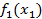 | |||||
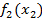 | |||||
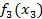 | |||||
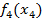 | |||||
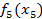 |
Распределить средства между предприятиями так, чтобы их суммарный доход был максимальным.
1. Заполним таблицу первой итерации.
Таблица №2
«Первая итерация»
| f1(x-x2) f2(x2) | ||||||
Строку f1 (x-x2) заполним данными первого субъекта f1(x1) из таблицы 1. Столбец f2(x2) заполним данными, соответствующими данным из таблицы 1.
Незаполненные элементы таблицы находятся путем сложения элементов строки f1 (x-x2) и столбца f2(x2) , т.е. по формуле:
FK(XK) + FK-1 (x-XK) (5)
где -некоторое количество субъектов, для которых определяются параметры и функция состояния;
x-сумма капитальных вложений, выделяемая нескольким субъектам.
2. Затем находим максимумы среди элементов, полученных в результате предыдущего шага, по побочным диагоналям таблицы (максимальные элементы выделены в таблице №2. Например, среди элементов диагонали 12,14,13,10 выберем 14.
3. После чего заполним новую таблицу данными, полученными в результате предыдущего шага. Строкаx2(x) заполняется элементами столбца ресурсов из таблицы 2, соответствующих максимальным элементам побочных диагоналей, полученным на шаге 3.
Таблица №3
«Максимальный прирост прибыли на первых двух предприятиях»
| x | |||||
| F2(x) | |||||
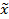 2(x) 2(x) |
4. Заполняем «вторую итерацию»
Таблица №4
«Вторая итерация»
| f2(x-x3) f3(x3) | ||||||
Строку f2 (x-x3) заполним данными строки F2(x) из таблицы №3. Столбец f3(x3) заполним данными, соответствующими данным из таблицы №1. Незаполненные элементы находим аналогично шагу 2 (формула 5).
5. Далее снова находим максимумы среди элементов, полученных в результате предыдущего шага, по побочным диагоналям таблицы (максимальные элементы выделены в таблице №4).
6. За тем снова заполним новую таблицу данными, полученными в результате предыдущего шага. Строка x3(x) заполняется элементами столбца ресурсов из таблицы 4, соответствующих максимальным элементам побочных диагоналей, полученных на данном шаге.
Таблица №5
«Максимальный прирост прибыли на первых двух предприятиях»
| x | |||||
| F2(x) | |||||
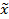 3(x) 3(x) |
7. Заполним таблицу третьей итерации.
Таблица №6
«Третья итерация»
| f3(x-x4) f4(x4) | ||||||
Строку 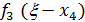 заполним данными строки
заполним данными строки 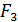 (x) из таблицы №3. Столбец f3(x3) заполним данными, соответствующими данным из таблицы №1. Незаполненные элементы находим аналогично шагу 2 (формула 5).
(x) из таблицы №3. Столбец f3(x3) заполним данными, соответствующими данным из таблицы №1. Незаполненные элементы находим аналогично шагу 2 (формула 5).
8. Далее снова находим максимумы среди элементов, полученных в результате предыдущего шага, по побочным диагоналям таблицы (максимальные элементы выделены в таблице №6).
9. За тем снова заполним новую таблицу данными, полученными в результате предыдущего шага. Строка x3(x) заполняется элементами столбца ресурсов из таблицы 6, соответствующих максимальным элементам побочных диагоналей, полученных на данном шаге.
Таблица №7
«Максимальный прирост прибыли на первых двух предприятиях»
| x | |||||
| F4(x) | |||||
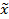 5(x) 5(x) | 1 / 0 | 1 / 2 |
10. Заполним «четвертую итерацию»
Таблица №8
«Четвертая итерация»
| f4(x-x5) f5(x5) | ||||||
Заполним последнюю диагональ таблицы путем сложения элементов (формула 5).
11. Находим максимальное число побочной диагонали, полученной на предыдущем шаге.
zmax=20 млн.рублей.
Делаем проверку так чтобы, средства между предприятиями и их суммарный доход был максимальным.
Пятому предприятию должно быть выделено (см. табл. 3.):
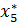 =
= 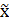 5(4)=0 млн. руб.
5(4)=0 млн. руб.
причем четвертому предприятию должно быть выделено :
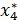 =
= 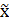 4(4-0)=
4(4-0)= 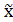 4(4)=1 млн. руб.
4(4)=1 млн. руб.
Тогда третьему предприятию должно быть выделено (см. табл. 5.):
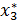 =
= 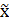 3(4-
3(4- 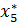 -
- 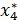 )=
)= 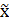 3(4-0-1)=
3(4-0-1)= 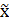 3(3)=1 млн. руб.
3(3)=1 млн. руб.
второму предприятию должно быть выделено (см. табл. 7.):
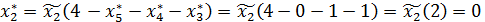 млн. руб.
млн. руб.
Hа долю первого предприятия остается:
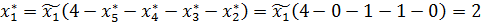 млн. руб.
млн. руб.
Таким образом, наилучшим является следующее распределение капитальных
вложений по предприятиям:
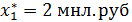
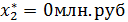
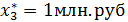
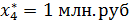
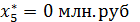
которое обеспечивает производственному объединению наибольший возможный прирост прибыли:
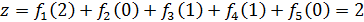 млн. руб.
млн. руб.
