Уравнения центральных поверхностей второго порядка

λ=0-точка

λ =1-эллипс,

λ.=-1-мнимый эллипс.

λ = 1-однополостный гиперболоид

λ =-1-двуполостный гиперболоид;

λ = 0 эллиптический конус.

Нецентральные поверхности

λ =l-эллиптический параболоид,

λ =-1 гиперболический параболоид.

2.Цилиндрические поверхности:

λ=1- эллиптический цилиндр,

λ=1- гиперболический цилиндр.

-мнимый эллиптический цилиндр(уравнению не удовлетворяет ни одна точка),

-пара плоскостей,

г) х² = 2ру, у² = 2рх, z² = 2рх , (1.6.12)

и т.д. параболические цилиндры.

Плоскости

х² = λа² , а ≠0, λ=1 пара параллельных плоскостей;

λ=-1 мнимые плоскости (уравнению не удовлетворяет ни одна точка пространства);

λ=0 - пара совпадающих плоскостей.

Пример 1.6.1. Записать каноническое уравнение кривой второго порядкаЗх²+4xу - 4х- 8y = 0 (сравните с решением примера 1.4.1 темы 1.4).

Квадратичная форма, содержащаяся среди слагаемых левой части уравнения имеет видF(x,y)= Зх²+ 4xy , а ее матрица

Вычислим собственные числа и собственные векторы матрицы А (см. тему 1.5)

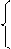Пусть собственные векторы Х_i(а₁⁽ⁱ⁾, а₂⁽ⁱ⁾) i.=1,2, где а₁⁽ⁱ⁾, а₂⁽ⁱ - коор­динаты. Система (1.5.5) для нахождения собственных векторов имеет вид

(3-λ)a₁+2a₂=0

2a₁-λa₂=0 (1.6.14)

Найдем собственные числа λ , решив характеристическое уравнение (1.5.6) .

Подставим первое собственное число λ₁=4 в систему (1.6.4).

и соответствующий единичный вектор X₁⁰ имеет вид

Подставим второе собственное число λ₂=-1 в систему (1.6.14):

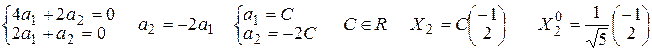
Перейдем в двумерное пространство R₂ к новому базису состав­ленному из собственных векторов матрицы А Х₁⁰ и Х₂⁰. При этом мат­рица квадратичной формы В в новом базисе будет иметь вид (1.5.3)

где матрица Т составлена из координат собственных векторов, запи­санных в столбцы. Связь между старыми координатами х, у (в базисе i, j ) и новыми координатами x₁, y₁ (в новом базисе) реализуется по формуле

квадратичная форма в новом базисе имеет вид (1.6.3) (случай двух переменных) F(x_1, y₁) = 4x₁² - у₁² .

Запишем равнение кривой второго порядка в новых координатах, приведем подобные.

Уравнение совпало с уравнением, полученным в примере 1.4.1. темы 1.4 и поэтому дальнейшие преобразования идентичны.

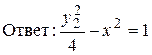
сопряженная гипербола с полуосями а=1, b=2.

Пример 1.6.2.Записать каноническое уравнение поверхности вто­рого порядка

11x² + 4ху + 2y² - 16xz + 20yz + 5z² + 6x + l2y -6=0.

Запишем квадратичную форму, входящую в состав левой части уравнения F(x,y,z)=llx^г + 4ху+2у² - 16xz + 20yz + 5z²

Собственные числа этой матрицы λ₁ = 9, λ₂ = l8, λ ₃ = -9 и единичные cобст-венные векторы X₁⁰ = (2/3, 2/3, 1/3)^T, X₂⁰ =(-2/3, 1/3, 2/3)^Т, X₃⁰=(1/3, -2/3, 2/3)^Т

найдены в примере 1.5.4 (см. тему 1.5). Связь между координатами x, y,z в старом базисе (i,j,k) и координатами x₁,y₁,z₁ в новом базисе (X₁⁰,X₂⁰,X₃⁰) имеет вид

Выше записанная матрица, как в примере 1.6.1,образована из коорди­нат собственных векторов, записанных в столбцы. Матрица квадратичной формы В в новом базисе - диагональная

F(x,y,z) =9x₁² +18y₁² -9z₁²

Запишем уравнение поверхности второго порядка в новых коорди­натах, приведем подобные члены и выделим полные квадраты

9x₁² +18y₁ ² - 9z₁² + 2(2x₁ - 2y₁ + z₁) + 4(2x₁ +y₁ -2z₁) - б = 0;

9x₁² + I8y₁² - 9z₁² +12x₁ - бz₁ - б = 0;

Перейдем к новым координатам (параллельный перенос):

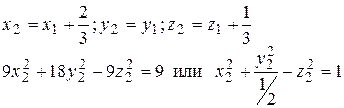
Полученное уравнение является каноническим уравнением однополо стного гиперболоида (1.6.7) с параметрами а =1, b =√2/2, с=1.

После изучения материала, содержащегося в разделе 1, студент должен выполнить контрольную работу N1.

Вопросы для самопроверки

1. Изобразите схематично основные поверхности второго порядка.

2. Может ли алгебраическая поверхность второго порядка представлять собою:

а) плоскость;

б) пустое множество?

Привести примеры.

3. Назовите типы и выпишите канонические уравнения цилиндрических поверхностей второго порядка.

4.Докажите, что всякое уравнение F(x,y,z)=0, где F-однородный многочлен второй степени, определяет конус с вершиной в начале ко­ординат.

После изучения тем 1.1-1.6 раздела 1 студенту необходимо вы­полнить контрольную работу № 1.