Логарифмическая функция

Логарифмическая функция Lnz, при z 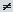0 определяется как обратная к показательной функции, причем

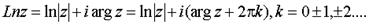
6. Общая степенная функция:

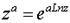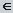, a C.

Эта функция многозначная, её главное значение равно .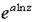

При a=1/n, n N получаем многозначную функцию – корень n-й степени из z:

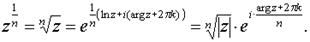
7. Функции, обратные к тригонометрическим и гиперболическим, являются многозначными и выражаются через логарифмическую.

a)

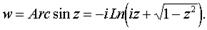
б)

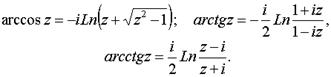
Вопрос 6

Интеграл ФКП определение и свойства интеграла ФКП

Пусть ФКП 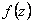определена в точках несамопересекающейся дуги 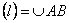, расположенной в 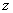–плоскости. Дуга 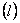ориентирована от точки 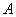к точке 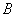, причем точка 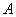соответствует 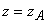, точка .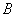

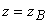Рассмотрим произвольное разбиение дуги 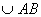системой точек 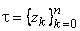такое, что 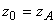, 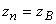и 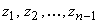упорядочены по длине дуги от точки 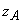до конечной точки разбиения .

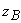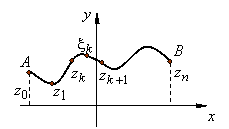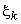Выберем на дуге произвольную систему точек так, чтобы точка лежала на дуге между точкам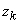и и 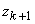(см. рисунок).

Сумма 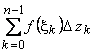, где 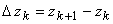, называется интегральной суммой функции 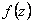по дуге 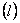, соответствующей разбиению 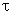и выбору точек системы 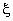, ее значение зависит от разбиения 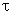и выбора точек .

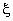Обозначим 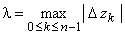– диаметр разбиения.

Интегралом ФКП 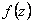по дуге 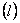называется число (вообще говоря, комплексное число), обозначаемое 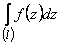и равное пределу интегральной суммы функци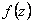и при 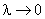, независимое от разбиения и выбора точек системы , т.е.

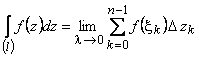. (1)

Доказано (см. [2]), что для непрерывной на дуге 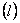ФКП 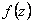и кусочно-гладкой дуги 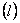интеграл (1) существует. Впредь будем предполагать эти условия выполненными.

Теорема Коши для односвязной области.Если D - односвязная ограниченная область, w = f( z) - аналитическая в этой области функция, то для любого кусочно-гладкого замкнутого контура L, лежащего в D, интеграл от f(z) по L равен нулю: .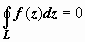
Доказательство. Удивительно, но эта важнейшая теорема непосредственно и просто следует из условий Коши-Римана и формулы Грина. Так как, по доказанному выше, 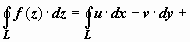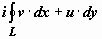, то, применяя к действительным криволинейным интегралам формулу Грина, получим 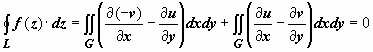вследствие условий Коши-Римана 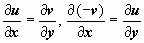. Символом G в доказательстве обозначена область, заключённая внутри контура L.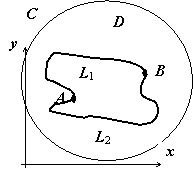
Следствие. Для всех кусочно-гладких кривых, лежащих внутри области D, в которой аналитична функция w = f(z), и имеющих общие начальную и конечную точки, интеграл 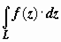имеет одинаковое значение.
Доказательство полностью повторяет доказательство Теоремы 1 раздела 16.3.3.5.1. Объединение L₁∪L₂⁻ кривых - замкнутый контур, поэтому .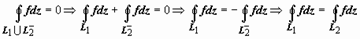
Оказывается, что справедлива и обратная теорема Морера: если функция w = f(z) непрерывна в односвязной области D и интеграл по любому замкнутому кусочно-гладкому контуру, лежащему в D, равен нулю, то функция аналитична в области D.

Вопрос 8 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ раздел математики, занимающийся главным образом алгебраическими операциями, производимыми над символами операции (или преобразования). Теория операторов. В задачу теории операторов входит подробное описание и классификация различных видов преобразований и их свойств, а также разработка символических методов, позволяющих минимизировать и упростить вычисления.
Пусть D и R - действительные линейные или векторные пространства, необязательно различные. Их элементами являются векторы, поэтому сумма двух элементов и произведение элемента на скаляр определены и удовлетворяют обычным условиям, предъявляемым к векторам. Существование конечных базисов в D и R необязательно. Пусть r, вектор из R, соответствует вектору d из D. Обозначим это соответствие T(d) = r или Td = r. Тогда T называется оператором с областью определения D и областью значений R. Оператор T является дистрибутивным, если

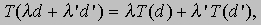
где l и l' - любые действительные числа, а d и d' - любые элементы из D. Если D и R - топологические векторные пространства, в которых ld и d + d' - непрерывные операции, то дистрибутивный непрерывный оператор называется линейным оператором. Если Q содержит D и R, то T2(d) определяется как T(T(d)) и аналогичным образом определяется Tn(d), если все эти операции имеют смысл. Двумя важными дистрибутивными операторами являются операторы дифференцирования p и интегрирования p-1. Элементами линейных пространств D и R в этом случае будут функции переменной x. Имеем

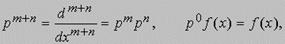
где m и n - неотрицательные целые числа. Так как интегрирование приводит к появлению произвольной постоянной, p-1p необязательно является тождественной операцией p0. Формальные правила комбинирования таких операторов восходят к Дж. Булю (1815-1864); например,

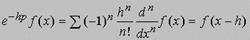по теореме Тейлора). В исчислении, пространство D ограничено областью определения функций f (x), тождественно равных нулю при отрицательных x. Главную роль играет функция 1(x), равная 0 при отрицательных x и 1 при неотрицательных x. Приведем некоторые "правила" исчисления Хевисайда:

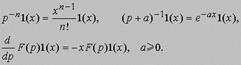Если n! заменить гамма-функцией Г(n + 1), то первое из правил останется в силе и при нецелых n.Основным результатом операционного исчисления принято считать теорему о композиции, или свертке, согласно которой, если F1(p)1(x) = f1(x) и F2(p)1(x) = f2(x), то

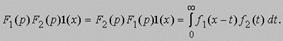Применяя теорему о свертке к pa при a № 0, -1, -2,..., можно определить интегрирование или дифференцирование дробного порядка. Например, рассмотрим выражение

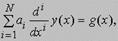
где функция y(x) и ее первые n - 1 производных обращаются в нуль при x = 0. Пусть y(x) = Y(p)1(x), g(x) = G(p)1(x). Примем

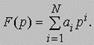
Предположим, что f (x) = F(p)-11(x). Тогда

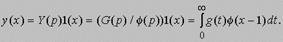Изображением по Лапласу функции-оригинала f (t) (или преобразованием Лапласафункции f (t)) называется функция комплексной переменной p, определяемая равенством
.
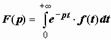Интеграл в правой части этого определения сходится абсолютно в любой точке p, удовлетворяющей неравенству Re p ≥ σ₁, где σ₁ - произвольной число, такое, что σ₁ > σ₀. Действительно, 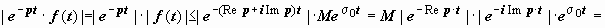(так как | e ^{−i Im p·t}| = | cos(Im p·t) − i sin(Im p·t)| = 1) =M | e ^{−Re p·t}|·e ^·σ₀^t = M e ^{−(Re p − σ}₀^{) t} ≤ M e ^−(σ₁ ^{− σ}₀^{) t}, а интеграл 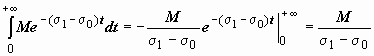сходится. Таким образом, мы доказали, что изображение F(p) определено в любой точке p, такой что Re p > σ₀, т.е. в полуплоскости справа от прямой Re p = σ₀. Как следствие, показатель скорости роста оригинала число σ₀ часто называют абсциссой сходимости.
Заметим, что мы доказали также, что 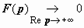: так как | e ^−pt·f (t)| ≤ M e ^{−(Re p − σ}₀^{) t}, то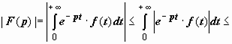 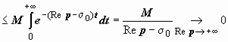. Кроме того, в оценке | e ^−pt·f (t)| ≤ M e ^−(σ₁ ^{− σ}₀^{) t} мы мажорировали модуль подынтегральной функции функцией, не зависящей от p, интеграл от которой сходится. Как и в теории функциональных рядов, этого достаточно, чтобы сходимость интеграла была равномерной по переменной p, поэтому функцию F(p) можно дифференцировать и интегрировать по этой переменной.

Вопрос 10

Теория вероятностей – математическая наука, изучающая закономерности в случайных явлениях. Одним из основных понятий теории вероятностей является понятие случайного события (или просто события).

Событием называется любой факт, который в результате опыта может произойти или не произойти. Примеры случайных событий: выпадение шестерки при подбрасывании игральной кости, отказ технического устройства, искажение сообщения при передаче его по каналу связи. С событиями связываются некоторые числа, характеризующие степень объективной возможности появления этих событий, называемые вероятностями событий.

К понятию «вероятность» существует несколько подходов.

Современное построение теории вероятностей основывается на аксиоматическом подходе и опирается на элементарные понятия теории множеств. Такой подход называется теоретико-множественным.

Пусть производится некоторый опыт со случайным исходом. Рассмотрим множество W всех возможных исходов опыта; каждый его элемент 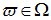будем называть элементарным событием, а множество Ω – пространством элементарных событий. Любое событие A в теоретико-множественной трактовке есть некоторое подмножество множества Ω: .

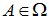Достоверным называется событие W, которое происходит в каждом опыте.

Невозможным называется событие Æ, которое в результате опыта произойти не может.

Несовместными называются события, которые в одном опыте не могут произойти одновременно.

Суммой (объединением) двух событий A и B (обозначается A+B, AÈB) называется такое событие, которое заключается в том, что происходит хотя бы одно из событий, т.е. A или B, или оба одновременно.

Произведением (пересечением) двух событий A и B (обозначается A×B, AÇB) называется такое событие, которое заключается в том, что происходят оба события A и B вместе.

Противоположным к событию A называется такое событие , которое заключается в том, что событие A не происходит.

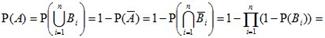
События A_k (k=1, 2, ..., n) образуют полную группу, если они попарно несовместны и в сумме образуют достоверное событие.

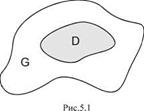Иногда недостаток конечного числа возможных исходов испытания можно преодолеть, используя геометрическое определение вероятности.

Рассмотрим некоторую замкнутую область G в пространстве (рис.5.1). Обозначим через 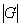ее меру. Если область – одномерная (отрезок), то мерой будет ее длина, если область двумерная (некоторая плоская фигура), то ее мера - площадь, если трехмерная (тело в пространстве), то – объем. Пусть область D полностью содержится в области G. Мера области D - .

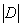Рассмотрим следующий эксперимент: случайно из области G выбирается точка А. Необходимо определить вероятность попадания точки А в подобласть D.

Роль элементарных событий в данном эксперименте играют точки области G. Все множество точек области Gобразует пространство элементарных событий. Все элементарные события – равновозможны, так как все точки области G равноправны в отношении попадания туда случайной точки A. Но число этих элементарных событий бесконечно. Поэтому в данном случае классическое определение вероятности не применимо.

Согласно геометрическому определению,

вероятность случайного события А равна отношению меры области, благоприятствующей появлению события А, к мере всей области, т.е.

.

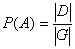Итак, статистическая вероятность случайного события А равна относительной частоте появления этого события в ряде испытаний, т.е.

,

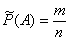где m – число испытаний, в которых появилось событие А;

n – общее число испытаний.

Это и есть статистическое определение вероятности.

Классическое определение вероятности

По классическому определению вероятность случайного события Р(А) равна отношению числа исходов, благоприятствующих А, к общему числу исходов, составляющих пространство элементарных событий, т.е.

.

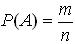(1.1)

Вычисление вероятностей при этом сводится к подсчету элементов того или иного множества и часто оказывается чисто комбинаторной задачей, иногда весьма трудной.

Классическое определение оправдано, когда существует возможность предсказания вероятности на основании симметрии условий, при которых происходит эксперимент, и вследствие этого симметрии исходов испытания, что приводит к понятию "равновозможности" исходов.

Вопрос 12

Формула полной вероятности и формула Байеса Если событие А может произойти только при выполнении одного из событий 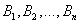, которые образуют полную группу несовместных событий, то вероятность события Авычисляется по формуле

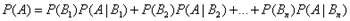.Эта формула называется формулой полной вероятности. Вновь рассмотрим полную группу несовместных событий 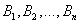, вероятности появления которых 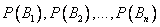. Событие А может произойти только вместе с каким-либо из событий 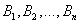, которые будем называть гипотезами. Тогда по формуле полной вероятности

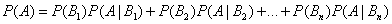
Если событие А произошло, то это может изменить вероятности гипотез 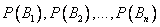. По теореме умножения вероятностей

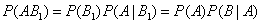, откуда

.

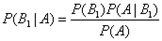Аналогично, для остальных гипотез

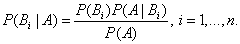
Полученная формула называется формулой Байеса (формулой Бейеса). Вероятности гипотез 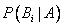называются апостериорными вероятностями, тогда как 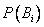-априорными вероятностями.

Вопрос 14Основные определения. Результат любого случайного эксперимента можно характеризовать качественно и количественно. Качественный результат случайного эксперимента – случайное событие. Любая количественная характеристика, которая в результате случайного эксперимента может принять одно из некоторого множества значений, - случайная величина. Случайная величинаявляется одним из центральных понятий теории вероятностей.

Пусть 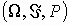- произвольное вероятностное пространство. Случайной величинойназывается действительная числовая функция x =x (w ), w W , такая, что при любом действительном x .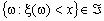

Событие 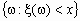принято записывать в виде x < x. В дальнейшем случайные величины будем обозначать строчными греческими буквами x , h , z , … Случайной величиной является число очков, выпавших при бросании игральной кости, или рост случайно выбранного из учебной группы студента. В первом случае мы имеем дело с дискретной случайной величиной (она принимает значения из дискретного числового множества M={1, 2, 3, 4, 5, 6} ; во втором случае - с непрерывной случайной величиной (она принимает значения из непрерывного числового множества - из промежутка числовой прямой=[100, 3000]). Функция распределения случайной величины. Её свойства Каждая случайная величина полностью определяется своей функцией распределения. Если x .- случайная величина, то функция F(x) = F_x (x) = P(x < x) называется функцией распределения случайной величины x . Здесь P(x < x) - вероятность того, что случайная величина x принимает значение, меньшее x. Важно понимать, что функция распределения является “паспортом” случайной величины: она содержит всю информация о случайной величине и поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением. Функция распределения любой случайной величины обладает следующими свойствами:

• F(x)определена на всей числовой прямой R;
• F(x)не убывает, т.е. если x₁ 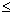x₂, то F(x₁) 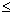F(x₂);
• F(- 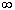)=0, F(+ 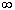)=1,т.е. 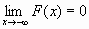и ;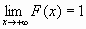
• F(x) непрерывна справа, т.е.

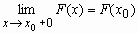
Функция распределения дискретной случайной величины Если x - дискретная случайная величина, принимающая значения x₁ < x₂ < … < x_i < … с вероятностями p₁ < p₂ < … < p_i < …, то таблица вида

x1	x2	…	xi	…
p1	p2	…	pi	…

называется распределением дискретной случайной величины. Функция распределения случайной величины, с таким распределением, имеет вид

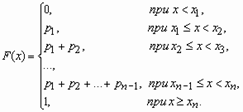
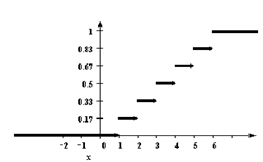
У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:

1/6	1/6	1/6	1/6	1/6	1/6

Функция распределения и плотность вероятности непрерывной случайной величины

Если функция распределения F_x (x) непрерывна, то случайная величина x называется непрерывной случайной величиной.

Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины p_x (x), которая связана с функцией распределения F_x (x) формулам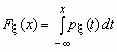и

и .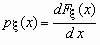

Отсюда, в частности, следует, что для любой случайной величины .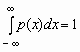

Вопрос 16

Каждая случайная величина полностью определяется своей функцией распределения. В то же время при решении практических задач достаточно знать несколько числовых параметров, которые позволяют представить основные особенности случайной величины в сжатой форме. К таким величинам относятся в первую очередь математическое ожидание и дисперсия. Математическое ожидание случайной величины Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx .

Математическое ожидание дискретной случайной величины x , имеющей распределение

x1	x2	...	xn
p1	p2	...	pn

называется величина 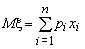, если число значений случайной величины конечно.

Если число значений случайной величины счетно, то 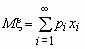. При этом, если ряд в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Математическое ожидание непрерывной случайной величины с плотностью вероятностей p_x(x) вычисляется по формуле 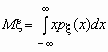. При этом, если интеграл в правой части равенства расходится, то говорят, что случайная величина x не имеет математического ожидания.

Если случайная величина h является функцией случайной величины x , h = f(x), то

.

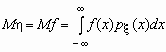Аналогичные формулы справедливы для функций дискретной случайной величины:

, .

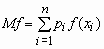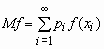Основные свойства математического ожидания:

• математическое ожидание константы равно этой константе, Mc=c ;

• математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин x , h и произвольных постоянных a и bсправедливо: M(ax + bh ) = a M(x )+ b M(h );

• математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(x h ) = M(x )M(h ).

Дисперсия случайной величины Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания. Если случайная величина x имеет математическое ожидание Mx , то дисперсией случайной величины x называется величина Dx = M(x - Mx )².Легко показать, что Dx = M(x - Mx )²= Mx ² - M(x )². Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина Mx ² >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам

, .

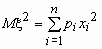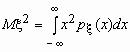Для определения меры разброса значений случайной величины часто используетсясреднеквадратичное отклонение 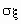,связанное с дисперсией соотношением .

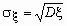Основные свойства дисперсии:

• дисперсия любой случайной величины неотрицательна, Dx 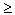0;

• дисперсия константы равна нулю, Dc=0;

• для произвольной константы D(cx ) = c²D(x );

• дисперсия суммы двух независимых случайных величинравна сумме их дисперсий: D(x ±h ) = D(x ) + D (h ).