Вопрос 34. Функция надежности

Пусть элемент начинает работать в начальный момент времени t₀=0. И работает до наступления отказа и обозначим через t время работы до наступления отказа.

Тогда если за время длительностью t произошёл отказ. То элемент проработал безотказно время меньшее чем t, тогда P(T<t) характеризует вероятность того, что элемент проработал безотказно время меньшее чем t. Тогда вероятность безотказной работы, в течение времени t.

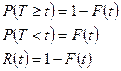(1)

Функция надежности R(t) представляет собой безотказную работу в течение времени t.

Показательная надежность

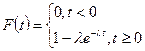
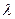-интенсивность отказов, среднее число отказов в единицу времени.

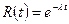(2)

Вопрос 35. Закон распределения вероятностей двумерной случайной величины.

распределения вероятностей случайной величины – перечень всевозможных пар значений вида:

(X;Y) (X_i;y_j) X=x_i Y=y_j и соответствующих им вероятностей.

Сумма всех вероятностей, стоящих в клетках = 1, т.к. все события вида:

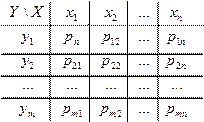X=x_i Y=y_j 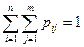P(X=x_i) = P(X=x_i , Y=y₁) + P(X=x_i , Y=y₂) + … + P(X=x_i , Y=y_m) = p_1i + p_2i + … + p_mi

P(Y=y_j) = p_j1 + p_j2 + … + p_jn

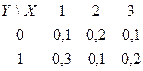
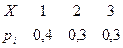
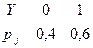
Функция распределения двумерной случайной величины.

(X,Y) F(x,y) = P(X<x , Y<y)

Свойства:

1)

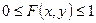
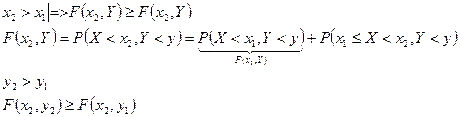2)

3)

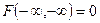
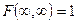
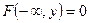
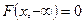
4)

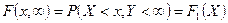
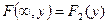
5)

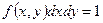
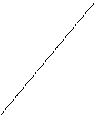
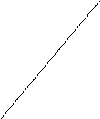
Вопрос 36. Вероятность попадания случайной величины в полуполосу.

Y

Y₁ (x₁,y₁) (x₂,y₁) P(x₁<X<x₂ , Y<y₁) = F(x₂ , y₁) - F(x₁ , y₁)

y

y₂ (x₁,y₂)

(x₁,y₁)

X₁ X₂ X y₁

X

X₁

P(X<x₁ , y₁<Y<y₂) = F(x₁ , y₁) - F(x₁ , y₁)

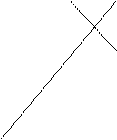
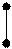Y₂ (x₁,y₂) (x₂,y₂) P(x₁<X<x₂ , y₁<Y<y₂) = F(x₂ , y₂) - F(x₁ , y₂) – [F(x₂ , y₁) - F(x₁ , y₁)] =

= F(x₁ , y₁) + F(x₂ , y₂) - F(x₁ , y₂) - F(x₂ , y₁) (*)

Y₁ (x₁,y₁) (x₂,y₁)

X₁ X₂

Вопрос 37. Плотность совместного распределения вероятностей непрерывной двумерной случайной величины.

Определение: Вторая смешанная частная производная от функции распределения.

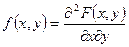(1) Вероятностный смысл совместной плотности распределения.

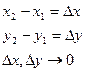
P_ABCD = [F(x₂ , y₂) - F(x₁ , y₂)] – [F(x₂ , y₁) - F(x₁ , y₁)] =

P_ABCD – вероятность попадания в плоскость. Воспользуемся формулой (1)

=

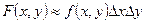
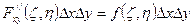
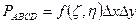(2)

Вероятностный смысл (2) – плотность распределения представляет собой:

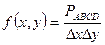
Y

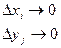
X

Тогда по формуле (2) Р попадания в каждый мелкий квадратик

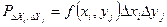
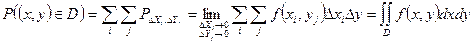
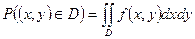(3)

Нахождение функции распределения по известной плотности.

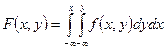
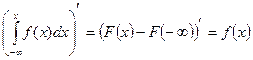
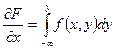
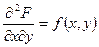
Свойства:

1) 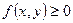Доказательство основано на вероятностном смысле плотности распределения.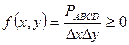

2)

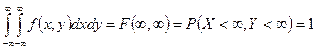
Вопрос 38. Нахождение плотностей вероятности составляющих двумерной случайной величины.

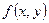
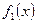
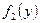
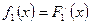
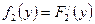
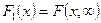
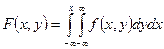
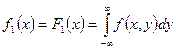
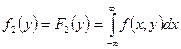
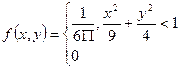
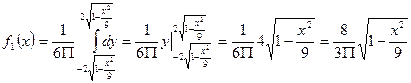
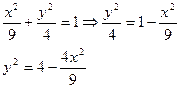
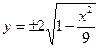
Вопрос 39. Зависимые и независимые случайные величины. Корреляционный момент и коэффициент корреляции.

Две случайные величины называют независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Отсюда следует, что условные распределения независимых величин равны их безусловным распределениям.