Сравнение функций и основные эквивалентности
Классификация простейших элементарных функций
Простейшими элементарными функциями обычно называют линейную (y=kx+b), квадратичную (y=ax2+bx+c), степенную (y=xn, где n целое число, не равно 1), показательную (y=ax,где a больше 0 и не равно 1), логарифмическую (y=loga x, где a больше 0 и не равно 1), тригонометрические (y=sin x, y=cos x, y=tg x, y=ctg x), обратные тригонометрические
(y=arcsin x, y=arccos x, y=arctg x, y=arcctg x).
К элементарным функциям относятся основные элементарные функции и те, которые можно образовать из них с помощью конечного числа операций (сложения, вычитания, умножения и деления) и суперпозиций.
Выделим классы функций, которые получены из элементарных:
- Целая рациональная функция (или многочлен): y=a0xn+a1xn-1+...+an, где n - целое неотрицательное число (степень многочлена), a0, a1, ..., an - постоянные числа (коэффициенты).
- Дробно-рациональная функция, которая является отношением двух целых рациональных функций.
Понятие одностороннего предела
Односторо́нний преде́л в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторо́нним преде́лом (или преде́лом сле́ва) и правосторо́нним преде́лом (преде́лом спра́ва).
Если функция f (x) имеет предел в точке a, то этот предел единственный.
Число A1 называется пределом функции f (x) слева в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех 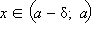 выполняется неравенство
выполняется неравенство 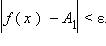
Число A2 называется пределом функции f (x) справа в точке a, если для каждого ε > 0 существует δ > 0 такое, что для всех 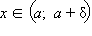 выполняется неравенство
выполняется неравенство 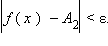
Предел слева обозначается 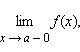 предел справа –
предел справа – 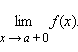 Эти пределы характеризуют поведение функции слева и справа от точки a. Их часто называют односторонними пределами. В обозначении односторонних пределов при x → 0обычно опускают первый нуль:
Эти пределы характеризуют поведение функции слева и справа от точки a. Их часто называют односторонними пределами. В обозначении односторонних пределов при x → 0обычно опускают первый нуль: 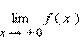 и
и 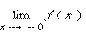 . Так, для функции
. Так, для функции 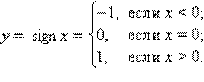
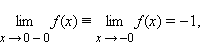
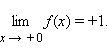
 11. Понятие предела на бесконечности
11. Понятие предела на бесконечности
Теоремы о пределах
Теорема 1. (о предельном переходе в равенстве)Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
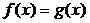 Þ
Þ 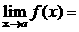
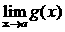 .
.
Теорема 2. (о предельном переходе в неравенстве)Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).
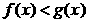 Þ
Þ 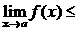
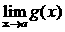 .
.
Теорема 3. Предел постоянной равен самой постоянной.
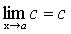 .
.
Доказательство. f(x)=с, докажем, что 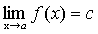 .
.
Возьмем произвольное e>0. В качестве d можно взять любое
положительное число. Тогда при 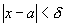
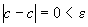 .
.
Теорема 4. Функция не может иметь двух различных пределов в
одной точке.
Доказательство. Предположим противное. Пусть
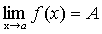 и
и 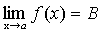 .
.
По теореме о связи предела и бесконечно малой функции:
f(x)-A= 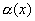 - б.м. при
- б.м. при 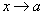 ,
,
f(x)-B= 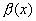 - б.м. при
- б.м. при 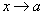 .
.
Вычитая эти равенства, получим: 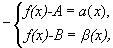
B-A= 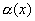 -
- 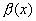 .
.
Переходя к пределам в обеих частях равенства при 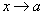 , имеем:
, имеем:
B-A=0, т.е. B=A. Получаем противоречие, доказывающее теорему.
Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при 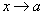 , то и алгебраическая сумма имеет предел при
, то и алгебраическая сумма имеет предел при 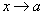 , причем предел алгебраической суммы равен алгебраической сумме пределов.
, причем предел алгебраической суммы равен алгебраической сумме пределов.
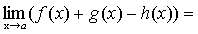
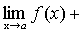
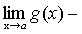
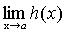 .
.
Доказательство. Пусть 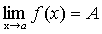 ,
, 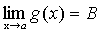 ,
, 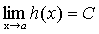 .
.
Тогда, по теореме о связи предела и б.м. функции:
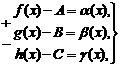 где
где 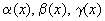 - б.м. при
- б.м. при 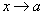 .
.
Сложим алгебраически эти равенства:
f(x)+g(x)-h(x)-(А+В-С)= 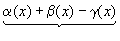 ,
,
где 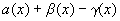 б.м. при
б.м. при 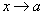 .
.
По теореме о связи предела и б.м. функции:
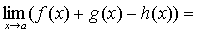 А+В-С=
А+В-С= 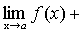
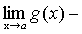
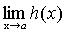 .
.
Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при 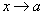 , то и произведение имеет предел при
, то и произведение имеет предел при 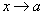 , причем предел произведения равен произведению пределов.
, причем предел произведения равен произведению пределов.
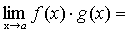
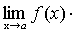
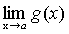 .
.
Следствие. Постоянный множитель можно выносить за знак предела.
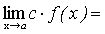
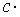
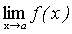 .
.
Теорема 7. Если функции f(x) и g(x) имеют предел при 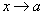 ,
,
причем 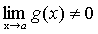 , то и их частное имеет предел при
, то и их частное имеет предел при 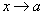 , причем предел частного равен частному пределов.
, причем предел частного равен частному пределов.
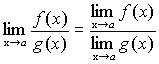 ,
, 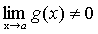 .
.
Замечательные пределы
Так называют следующие равенства:
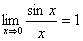 – первый замечательный предел;
– первый замечательный предел;
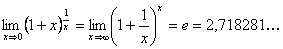 – второй замечательный предел.
– второй замечательный предел.
Они замечательны тем, что помогают вычислению многих других пределов.
Сравнение функций и основные эквивалентности
