Дифференциальные уравнения

1. Задачи, приводящие к дифференциальным уравнениям. Основные понятия. Задача Коши. Теорема существования и единственности решения задачи Коши.

2. Дифференциальные уравнения с разделяющимися переменными, однородные уравнения первого порядка. Линейные уравнения и уравнения Бернулли.

3. Дифференциальные уравнения высших порядков. Задача Коши. Понятие о краевых задачах дифференциальных уравнений. Уравнения, допускающие понижения порядка.

4. Линейные уравнения, высшего порядка однородные и неоднородные. Понятие общего решения.

5. Линейные неоднородные уравнения с постоянными коэффициентами. Метод неопределенных коэффициентов. Метод вариации произвольных постоянных.

6. Нормальная система дифференциальных уравнений. Задача Коши для нормальной системы дифференциальных уравнений. Теорема существования и единственности решения задачи Коши. Решение систем линейных дифференциальных уравнений с постоянными коэффициентами методом исключения.

Ряды

1. Числовые ряды. Основные понятия. Сходимость и сумма ряда. Необходимое условие сходимости. Действия с рядами.

2. Достаточные условия сходимости числовых рядов.

3. Знакочередующиеся ряды. Ряд Лейбница и его приложения к приближенным вычислениям. 4. Функциональные ряды. Область сходимости, методы ее определения.

5. Степенные ряды. Ряды Тейлора. Ряды Маклорена. Применение степенных рядов в приближенных вычислениях. Разложение функции в степенные ряды.

6. Тригонометрические ряды Фурье. Теорема Дирихле. Разложение функции в ряд Фурье.

Разложение в ряд Фурье четных и нечетных функций.

Специальные главы высшей математики

Теория функции комплексного переменного

1. ФКП. Основные понятия. Предел и непрерывность ФКП. Основные элементарные функции комплексного переменного.

2. Дифференцирование функции комплексного переменного. Условия Коши-Римана. Аналитическая функция.

3. Интегрирование функции комплексного переменного.

4. Ряды в комплексной плоскости (Ряд Лорана, ряд Фурье).

5. Классификация особых точек. Вычет функции.

Операционное исчисление

1. Основные понятия операционного исчисления. Преобразование Лапласа.

2. Основные теоремы операционного исчисления.

3. Применение операционного исчисления к решению дифференциальных уравнений.

Контрольная работа №2 «Дифференциальные уравнения. Ряды. Спец.главы высшей математики».

№№ 321-340; 341-350; 371-380; 381-390; 391-44; 431-440; 461-470.

Вопросы для контроля остаточных знаний.

1. Вычислить: .

2. Найти производную от функции: .

3. Вычислить: .

4. Исследовать ряд на сходимость: .

5. Найти общее решение уравнения: .

6. Вычислить: , где ограничена линиями:

7. Найти частные производные и от функции .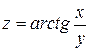

8. Найти изображение функции .

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1. Письменный Д.Т. Конспект лекций по высшей математике. М.: Рольф, 2001.

2. Амосов А.А. Вычислительные методы для инженеров. М; Высш.шк; 1994. (уч.пособие).

3. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. М., Наука, 1984.

4. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление.М., Наука, 1988.

М., Наука, 1985.

5. Бугров Я.С., Никольский С.М. Высшая математика: Задачник, М., Наука, 1982.

6. Бутузов В.Ф. и др. Математический анализ в вопросах и задачах. М., Высш.шк., 1993.

статистика. М., Высш.шк., 1982.

7. Кудрявцев Л.Д. Краткий курс математического анализа. М., Наука , 1989.

8. Сборник задач по математике для втузов под ред. Ефимова А.В. М., Наука,

ч.1-2, 1993-1994.

9. Общие указания и контрольные задания для студентов заочной формы обучения. Методические указания. Чита. ЧитГУ, 1998.

Программу составила: доцент Лескова Г.А.