Для несовместных событий вероятность их суммы равна сумме

Их вероятностей

Р(А+В)= 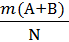= = 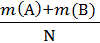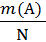+ 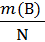= Р(А)+Р(В).

3. Для полного набора событий их сумма - достоверное событие, т.е.

Р( )= = 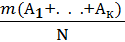= =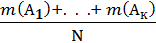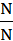1.

Отсюда для несовместных событий А и В ввиду отсутствия благоприятных исходов находим Р(АВ)=0 .

Далее, учитывая, что А+ 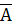=Ω, вследствие несовместности события и ему противоположного получаем

Р(А+ 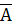)=Р(А)+Р( 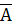)=1 или Р( 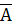)=1-Р(А).

В качестве примера рассмотрим бросание кубика. При условии полной симметрии кубика вероятность выпадения любой его грани равна 1/6. Поэтому для события А=”выпало четное число” из расчета три благоприятных исхода из шести возможных имеем Р(А)=3/6=1/2=0,5.

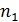	1 2 3 4 5 6
	2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 7 8 9 5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 1011 12

Если бросать два кубика одновременно, то для события В=”сумма выпавших цифр равна 10” общее количестве исходов равно 6´6=36, поскольку каждый исход на первом кубике может комбинировать с любым исходом на втором кубике. Для того чтобы убедиться в этом достаточно составить таблицу с перечислением всевозможных исходов с обозначением символам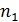и и цифр, выпавших на первом и втором кубиках соответственно. Из этой таблицы сразу же извлекаются благоприятные исходы в количестве трех штук: (6, 4), (5, 5), (4, 6). Теперь нетрудно посчитать, что Р(В)= 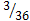= 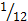. Полученный результат трактуется так, - в реальном эксперименте на каждые 12 испытаний в среднем придется лишь один благоприятный исход.

2. 7. Схемы случайных экспериментов

Многие случайные события моделируются экспериментами с извлечением перенумерованных или разноцветных шаров из урны. Шары можно извлекать с учетом или без учета их номеров. После извлечения шар в урну можно вернуть, а можно этого не делать. Поэтому различают соответствующие схемы выбора, в каждой из которых общее число исходов и благоприятных исходов подсчитывается по-разному.

Сначала посчитаем количество перестановок в совокупности из n перенумерованных шаров. Для выбора первого шара имеется n возможностей. Второй шар может быть выбран уже только n-1 способом и т.д. Поскольку каждый способ выбора первого шара может комбинировать со всеми способами выбора остальных шаров, то число перестановок в группе из n перенумерованных шаров равно

N=n(n-1)(n-2) . . . 3·2·1=n!.

Для произведения последовательности чисел от 1 до n здесь использовано стандартное обозначение n!, которое читается как “n факториал”.

2.7.1. Схема без возвращения с упорядочением

Из урны с n шарами извлекается m шаров по одному без возвращения, при этом порядок важен, т. е. какой шар окажется на первом, втором и т. д. местах имеет принципиальное значение.Первый шар может быть выбран n способами, второй n-1 способами (выбор из n-1 шара) и т. д. и, наконец, последний m-й шар - n-m+1 способами. Поскольку выбор шара на каждом шаге может комбинировать со всеми способами выбора остальных шаров, то общее количество возможных вариантов составляет

N=n(n-1)...[n-m+1] = = = .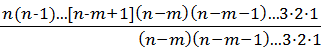

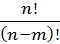Величина , известная под названием “число размещений из nэлементов по m”, получена путем умножения и деления исходного выражения на одно и то же значение (n- m)!. Начальная часть формулы для случая m =n дает уже полученный ранее результат N=n!, а при m =0 из последней части формулы находим N=1, т.е. ни один элемент из любой совокупности может быть извлечен одним единственным способом, что совершенно очевидно. Таким образом = n!, = 1.

	1 2 3 4 5 6
	- 12 13 1415 16 21- 23 24 25 26 31 32 - 34 35 36 41 42 43 - 45 46 51 52 53 54 - 56 61 62 6364 65 -

Пример. Какова вероятность того, что последовательное расположение номеров двух шаров, наугад извлеченных без возвращения один за другим из урны с шестью перенумерованными шарами, даст двузначное число, кратное 7, т.е. делящееся на семь нацело. Таким образом, вводя соответствующие обозначения будем искать Р(“ 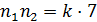”), где 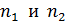- номера первого и второго шаров, а 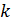- натуральное число. В помощь решению задачи составим таблицу всех мыслимых исходов. Всего исходов N = 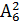= 6·5 = 30, что подтверждает таблица, при шести благоприятных исходах - по одному в каждой строке таблицы: 14, 21, 35, 42, 56, 63. Тогда искомая вероятность

Р(“ 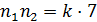”) = = = 20%,

что не так уж и мало.

2. 7.2. Схема без возвращения и без упорядочения

При извлечении из урны с n шарами mшаров одного за другим их порядок не имеет значения, т.е. выборки отличаются только составом. В этих условиях комбинации (1, 2) и (2, 1) в отличие от предыдущего примера становятся неразличимыми. Подобная ситуация может возникнуть, если на экзамене преподаватель по доброте душевной разрешает вытащить сразу два билета и тогда для студента по существу важна только его способность ответить на вопросы этих билетов и безразлично какая комбинация номеров ему досталась (3, 7) или (7, 3).

В совокупности из m шаров возможно произвести m! перестановок, которые по условию неразличимы между собой. Поэтому общее количество вариантов (исходов) по сравнению с предыдущей схемой должно быть меньше в m! раз и составит

N = = = .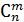

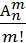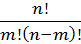Величина 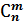называется числом сочетаний из n элементов по m.

Для обеспечения дееспособности данной формулы при всех целых 0£m£n чисто формально принимается 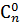= = 1, поскольку не выбрать ни одного элемента (m=0) или выбрать все элементы из любой совокупности (m=n) в рассматриваемых условиях можно только одним способом.

Пример.В урне находится 7 черных шаров и 3 белых. Какова вероятность события А=”из 4-х наугадизвлеченных шаров ровно 2 будут белыми”.

В силу отличия различных комбинаций из 4-х шаров исключительно одним составом всего исходов насчитывается

N = = = 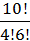= 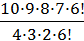210.

Количество способов выбора двух белых и черных шаров равно соответственно = 3 и = 21. Поскольку каждый вариант выбора белых шаров может сочетаться с любым вариантом выбора черных шаров, то число благоприятных исходов выразится величиной 3·21=63 и, тогда,

Р(А) = = 0,3.

2. 7.3. Схема с возвращением и с упорядочением

N = n· n· . . . · n = .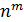

Из урны с n шарами m раз повторяется процедура извлечения шара и его возвращения обратно с фиксацией порядка вытащенных шаров. На каждом шаге такого эксперимента ситуация одна и та же - выбирается любой из n шаров, что естественно может быть сделано n способами. В результате опыта образуется набор из m шаров, в котором каждый шар может комбинировать с каждым, в том числе и с самим собой. Всего возможных исходов

m

Пример. Из телефонной книги с 7-значными номерами наугад выбирается номер. Найти вероятность того, что все цифры в номере различны, если все комбинации цифр в номере равновозможны. Иными словами условиями задачи с целью упрощения допускаются номера 0000000, 0001111, 1010101 и т.п.

Общее количество номеров в такой схеме N= 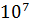= 10000000.

Благоприятные исходы представляют наборы из 7 цифр, отличающиеся не только самими цифрами, но и их порядком. Тогда количество благоприятных исходов определяется числом размещений m = и потому

Р(А) = 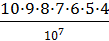≈ 0,06=6%.

2.7.4. Схема с возвращением без упорядочения

Из урны с n шарами m раз извлекается шар и возвращается обратно без учета порядка. В результате эксперимента образуются комбинации из m шаров, отличающиеся только своим составом. Такой опыт эквивалентен извлечению одновременно m шаров из урны с n +m -1 шарами c подсчетом общего числа исходов с помощью числа сочетаний. Здесь “-1” образуется вследствие того, что возвращение последнего шара в урну уже никак не может повлиять на результат. Убедиться в этом помогает пример выбора одного единственного шара, что может быть сделано n способами. При этом 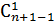= = 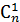= 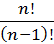n, как тому и следует быть.

Пример. Покупатель в кондитерской выбил чек на 4 пирожных из 7 видов, имеющихся в продаже. Какова вероятность того, что куплены пирожные: одного вида (событие А); разных видов (В); две пары разных видов (С). Содержание данной задачи соответствует схеме выбора с возвращением без упорядочения. В самом деле, купив один эклер можно купить и второй (возвращение) и при этом, какой из них куплен первым не имеет ровным счетом никакого значения.

Общее количество исходов составляет N= 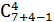= =210.

Число благоприятных исходов для события А определяется исходя из общего количества разных видов пирожных m(А)=7 и потому

Р(А) = = .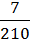

Во втором случае благоприятными являются наборы из 4-х различных пирожных, отличающиеся только составом, т.е. m(В)= 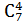=35 и, следовательно,

Р(В) = = .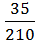

Поскольку из 7 элементов можно сгруппировать =21 различную пару, то событие С реализуется с вероятностью

Р(С) = = .

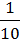	1 2 3 4 5 6 7
	- 12 13 1415 16 17 - - 23 24 25 26 27 - - - 34 35 36 37 - - - - 45 46 47 - - - - - 56 57 - - - - - - 67 - - - - - - -

Для того, чтобы убедиться в правильности подсчета количества благоприятных исходов достаточно составить таблицу с их перечислением, предварительно перенумеровав все 7 видов пирожных и обозначив символам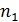и и номера первой и второй пары. Полученный результат свидетельствует, что наиболее вероятным является событие В.

2. 8. Геометрическая вероятность

Одним из классических экспериментов теории вероятностей является “вбрасывание точки” в некоторую геометрическую замкнутую область. Для определенности зададим на плоскости квадрат со стороной равной 1 и обозначим его Ω. В этот квадрат наугад вбрасывается точка и

0.7 1

0.5 0,5

Ω

А

гарантированно в него попадает. Более того, предполагается, что все точки квадрата равноправны и потому все исходы такого эксперимента равновозможны в смысле попадания в любую точку Ω. Эксперимент имеет бесконечное множество равновозможных и несовместных исходов, каждый из которых отождествляется с точкой квадрата с координатами (𝑥, 𝑦). Обозначим А некоторую подобласть Ω, как это показано на рисунке, и будем считать событием А попадание в одноименную область. Прозвучавшие выше термины равновозможности, несовместности и благоприятности свидетельствуют, что мы уже совсем близки к применению формулы классической вероятности. Осталось только конкретизировать способ численного определения количества благоприятных исходов и всех мыслимых исходов. Поскольку в качестве интегральных числовых характеристик этих исходов реально мы располагаем только размерами одноименных площадей, то количество исходов каждого вида отождествляется с соответствующими площадями. При этом площадь квадрата S(Ω) выражает общее количество исходов, а S(А) - число благоприятных исходов. Тогда в соответствии с определением классической вероятности как отношения числа благоприятных исходов к общему количеству равновозможных и несовместных исходов для расчета так называемой геометрической вероятности события А получаем формулу

Р(А) = .

Применительно к ситуации, изображенной на рисунке, находим

Р(А) = 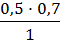= 0,35.

Геометрическая вероятность обладает всеми свойствами классической вероятности:

- отношение площади вложенной фигуры А к площади Ω неотри-

цательно и не превосходит 1;

- несовместным событиям отвечают непересекающиеся области и

потому их сумме соответствует суммарная площадь;

- полному набору событий соответствует разбиение Ω на непересе-

кающиеся области, дающие в своем объединении Ω.

Для иллюстрации практического применения геометрической вероятности рассмотрим следующую задачу: юноша и девушка договорились о встрече между 19 и 20 часами, поклялись непременно придти и условились, что один ждет другого только 15 мин, а затем уходит. Какова вероятность их встречи.

Преодолев первоначальное замешательство от такой постановки вопроса, напряжем свои логические способности. Очевидно, что сначала надо выжать все возможное из имеющихся исходных данных и затем распорядиться полученной информацией сообразно ее содержанию. Итак, интервал встречи составляет 1 час. Поскольку влюбленные гарантированно приходят в этот интервал времени, то разумно обозначить время их прихода в долях часа: 𝑥 - пришел юноша; 𝑦 - пришла девушка. Тогда 0 , . По условию задачи для встречи необходимо, чтобы разность между моментами их прихода вне зависимости от того кто пришел первым не превышала часа, т.е. . При наличии двух параметров 𝑥 и 𝑦в голову сразу же приходит мысль о декартовой системе координат, в которой моменты прихода изобразятся на плоскости точкой (𝑥 , 𝑦) с соответствующими координатами. Причем все точки улягутся точно в квадрат с единичной стороной. Например, если юноша и девушка пришли в 19.30 и 19.40, то такая ситуация отождествится с точкой квадрата ( 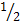, 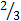). Далее, займемся препарированием модульного неравенства и с помощью школьных знаний без большого труда получим два неравенства:

которые в своей совокупности устанавливают ограничения на возможные изменения параметра 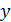: 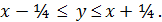Обратившись к разделу “Линейное программирование” п. 5.6 нетрудно установить, что это двойное неравенство задает на плоскости область между двумя прямым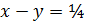и : , и : - 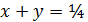, ограниченную

0,5

Ω

0,5

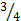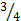В

еще к тому же рамками квадрата Ω. В самом деле, построив эти прямые по двум точкам их пересечения со сторонами Ω

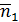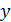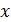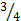{ : ( , 0), (1, )}, { : (0, ), ( , 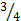1) }, и определив с помощью их нормальных векторов 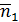=(1, -1) и =( -1, 1) зоны действия соответствующих неравенств получим фигуру В, обозначенную на рисунке штриховкой. Каждая точка В гарантирует встречу молодых людей,

т.е. является благоприятной для одноименного события В=”встреча состоялась”. Теперь для решения задачи с полным основанием можно применить формулу геометрической вероятности. Площадь фигуры В удобно вычислить как разность площади Ω и общей площади двух не заштрихованных треугольников, которые будучи сложенными вместе по гипотенузе дадут квадрат со стороной 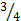. Тогда

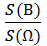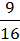Р(В) = = = 1- = < = 50%.

Полученный результат свидетельствует, что при заданных исходных данных вероятность встречи молодых людей несколько меньше 0.5, т.е. встреча скорее не произойдет, нежели состоится.

Таким образом, задача о встрече успешно решена с помощью изначально не очевидных, но простых геометрических построений. Рассмотренный пример изящного применения аппарата ТВ вкупе с приведенными выше схемами выбора шаров из урны демонстрируют широту и мощь прикладных возможностей этой науки.

А

В

АВ

Ранее говорилось, что вероятность суммы двух несовместных случайных событий равна сумме их вероятностей. Геометрическая вероятность помогает установить правило вычисления вероятности суммы двух событий в случае их совместности. Для начала вспомним иллюстрацию этой ситуации кругами Эйлера в случае совместности случайных событий. Здесь АВ - произведение соответствующих событий. Очевидно, что S(А+В) = S(А)+S(В)-S(АВ),

поскольку при сложении площадей А и В площадь их пересечения АВ будет учтена дважды - в составе А и В. Поэтому следуя принципам геометрической вероятности в случае совместности случайных событий получаем

Р(А+В)=Р(А)+Р(В)-Р(АВ)

и если события несовместны, то в силу Р(АВ)=0 данная формула превращается в полученное ранее правило - “вероятность суммы двух несовместных случайных событий равна сумме их вероятностей”. В¹ противном случае в этой формуле появляется поправочный член, учитывающий совместность случайных событий в виде вероятности их произведения. Хотя данная формула верна в общем случае приведенные здесь рассуждения не являются строгим доказательством и скорее могут рассматриваться в качестве мнемонического правила.

2.9.Условная вероятность

Информация, полученная в ходе случайного эксперимента, может изменить вероятность некоторых исходов в последующих испытаниях. Например, если из урны с несколькими разноцветными шарами извлечен единственный имеющийся в ней черный шар, то вероятность достать потом еще один черный шар равна нулю.

Вероятность события А при условии, что произошло событие В, называется условной и обозначается Р(А|В).

Если при бросании кубика А=”выпало 2”, В=”выпало четное число”, С=”выпало 3”, то

Р(А) = Р(С) = , Р(В) = 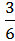= , однако Р(А|В) = , Р(А|С) = 0.

На этом примере видно, что в случайном эксперименте с N равновозможными и несовместными исходами при расчете вероятности события А при условии, что произошло событие В общее число исходов сокращается до количества исходов благоприятствующих В. Иными словами событие А рассматривается на фоне В. Таким образом за общее число исходов принимается количество исходов благоприятных для В, а за количество исходов благоприятных для А берется число исходов благоприятных для А и В одновременно, т.е. благоприятных для произведе-

ния АВ.