Элементарные булевы функции от двух переменных

Глава III. Алгебра логики.

(Лекция 7)

Функции алгебры логики

E₂ = {0, 1}

Определение. Функцией алгебры логики называется отображение f: ® E₂, где x_i Î E₂, i = 1, 2, …, n. Функции алгебры множеств называются булевыми функциями. Обозначим все множество булевых функций через P₂(n).

Теорема (О количестве булевых функций от n переменных):

Мощность множества булевых функций |P₂(n)| = .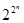

Доказательство: (Следует из Теоремы о мощности всех подмножеств данного множества)

Пример: |P₂(4)| = = 2¹⁶ = 65536

Существенные и фиктивные переменные

Определение. Функция f(x₁, x₂, … x_i-1, x_i, x_i+1, … x_n) существенно зависит от переменной x_i, если существует набор a₁, …, a_n переменных x₁, …, x_n, что выполняется неравенство:

f(x₁, x₂, … x_i-1, 0, x_i+1, … x_n) ¹ f(x₁, x₂, … x_i-1, 1, x_i+1, … x_n).

В этом случае переменную x_i называют существенной. Если же x_i не является существенной, то ее называют фиктивной.

Определение. Переменную x_i называют фиктивной, если для любого набора значений a₁, …, a_n переменных x₁, …, x_n выполняется равенство: f(x₁, x₂, … x_i-1, 0, x_i+1, … x_n) = f(x₁, x₂, … x_i-1, 1, x_i+1, … x_n).

Примеры:

1) f(x₁, … x_n) º 0 Þ "x_i – фиктивная, i = 1, 2, …, n.

2)

x	y	f(x, y)

f(0, 0) ¹ f(0,1) Þ Переменная x – существенная

f(0, 0) = f(1,0) ü

f(0, 1) = f(1,1) þÞ Переменная y – фиктивная

Исключение и введение фиктивных переменных

Пусть для функции f(x₁, … x_n) переменная x_i – фиктивная. Ее можно исключить и перейти к булевой функции g(x₁, x₂, … x_i-1, x_i+1, … x_n) с n – 1 переменной. Для этого в таблице для функций вычеркнем все строки, соответствующие значениям x_i = 1 и столбец для аргумента x_i. Полученная таблица будет определять функцию g(x₁, x₂, … x_i-1, x_i+1, … x_n). При этом говорят, что функция g получена из функции f исключением фиктивной переменной x_i. Кроме того, можно сказать, что f получена из g введением фиктивной переменной x_i.

Равенство функций

Определение. Две функции называются равными, если на каждом наборе переменных значения функций совпадают.

Пример:

x	y	f(x, y)				x	g(x)

g(y) = f(x, y)

Вывод: Если одна функция получена из другой исключением или введением фиктивной переменной, то такие функции являются равными.

Замечание:

1) Существует два типа функций, которые не имеют существенных переменных. Это функции-константы: 0 и 1. Поэтому целесообразно считать эти функции зависящими от пустого множества существенных переменных.

2) Если дана конечная система булевых функций {f₁, …, f_s}Ì P₂, то можно считать, что все s функций зависят от одних и тех же переменных.

В Алгебре логики некоторые функции принято считать элементарными.

Элементарные булевы функции от одной переменной

x	x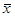

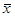- инверсия (отрицание) x

Элементарные булевы функции от двух переменных

x	y	x & y	x Ú y	x ~ y	x Å y	x ® y	x / y	x ¯ y

x & y – конъюнкция (логическое умножение)

(x & y = 1 Û x = 1 Ù y = 1)

x Ú y – дизъюнкция (логическое сложение)

(x Ú y = 0 Û x = 0 Ù y = 0)

x ~ y – эквивалентность

(x ~ y = 1 Û x = y)

x Å y – сумма по модулю 2 (разделительная дизъюнкция) ( )

(x Å y = 0 Û x = y)

x ® y – импликация (логическое следование)

x / y – штрих Шеффера (антиконъюнкция) ( )

x ¯ y – стрелка Пирса (антидизъюнкция, функция Вебба, функция Даггера) ( )