Формула умножения вероятностей

Теорема: Вероят-ть совместного появ-ния двух незав. соб-тий= произведению этих же соб-тий: Р(АВ)=Р(А)Р(В)

Теорема: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие имело место:

.

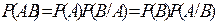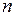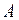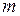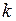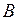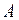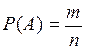Доказательство: Предположим, что из возможных элементарных исходов событию благоприятствуют исходов, из которых исходов благоприятствуют событию . Тогда вероятность события будет , условная вероятность события 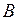относительно события 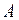будет .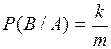

Произведению событи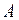й и 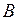благоприятствуют только те исходы, которые благоприятствуют и событию 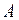, и событию 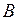одновременно, т.е. 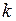исходов. Поэтому вероятность произведения событи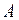й и .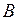

Умножив числитель и знаменатель этой дроби на 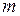, получим:

.

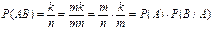Аналогично доказывается и формула .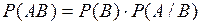

Теорему умножения вероятностей легко обобщить на любое конечное число событий.

10. Формула полной вероятности:

Пусть H1…Hn – полная группа событий и P(Hi)>0, i=1,n⁻⁻, тогда для любого события А

Р(А)= )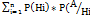

Формула полной вероятности и формула Байеса. По теореме сложения вероятностей несовместных событий 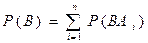. Используя теорему умножения вероятностей, находим:

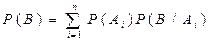. Полученная формула называется формулой полной вероятности.

11. На основании теоремы о вероятности произведения двух событий:

,

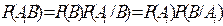откуда:

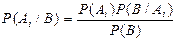
или

.

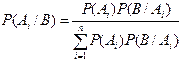Полученная формула носит название формулы Байеса.

Формула Байеса:

Пусть дана полная группа событий H1,…,Нn и некоторое событие А, тогда для любых К от 1 до n условная вероятность события Нк при условии, что произошло событие А вычислится по формуле

Р(Нк/A)=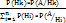

12. Схема Бернулли последовательных испытаний. Формула Бернулли и ее следствие. Наивероятнейшее число наступлений события.

Схема Бернулли заключ. в след.: проводится n последовательных испытаний, которые

1)независимы;

2)в любом испытании возможны только 2 исхода (A и );

3)вероятности этих исходов постоянны и не изменяются от испытания к испытанию.

Под независимыми понимаются такие эксперименты, в которых любые события, возникающие в разных экспериментах, являются независимыми в совокупности.

p = P(A) q = P( ) = 1 – p

Наступление события A обычно называют успехом, а ненаступление – неудачей.

Формула Бернулли.

Вероятность того, что в схеме Бернулли из n испытаний успех наступит ровно m раз равна 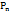(m) =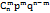

Следствие: Пусть m₁ и m₂ 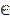Z, 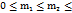n. Тогда вероятность того, что в схеме Бернулли успех наступит не менее m₁ и не более m₂ раз в n испытаниях равна

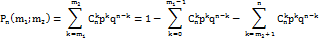
Определение: Число наступлений события A (успеха) называется наивероятнейшим, если оно имеет наибольшую вероятность по сравнению с вероятностями наступления события A любое другое количество раз.

Теорема. Наивероятнейшее число наступлений события 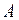в 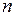независимых испытаниях схемы Бернулли заключено между числам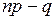и и 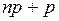. При этом, если 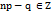, то наивероятнейших чисел два, а именно 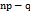и .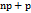

13. В случае, когда число испытаний велико, формулу Бернулли применять неудобно. Для больших 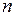существуют приближенные формулы. Точность этих формул увеличивается с возрастанием .

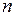Теорема Пуассона:

Предположим, что произведение np = 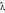является постоянной величиной, когда n неограниченно возрастает, тогда для любого фиксированного m и 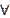постоянного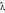

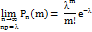
На практике эта теорема применяется следующим образом. Если n велико, а p мало,

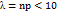, то

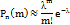
Теорема Пуассона с оценкой погрешности: Пусть 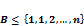произвольное множество целых неотрицательных чисел от 0 до n, 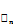– число успехов n испытаний схемы Бернулли, тогда

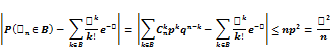
Замечание: Если мало значение q₁ то по Пуассоновским приближениям можно воспользоваться для числа неудач.

14. Если же n достаточно велико, а p не слишком близко к нулю или единице, то имеет место теорема Муавра-Лапласа:

,

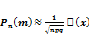где 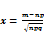, а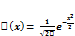

Функция 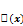называется ф-ей Гауса. Эта функция затабулирована

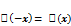– ф-ия Гауса чётная.

При достаточно больших n вероятность того, что событие A в схеме Бернулли наступило не менее m₁ и не более m₂ раз в n испытаниях, при условии, что p не слишком близко к 0 или 1, вычисляется с помощью след. теоремы:

Интегральная теорема Муавра-Лапласа:

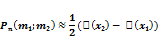
где ,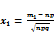

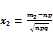
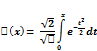
Ф-ия 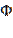(x) называется ф-ией Лапласа, она также затабулирована, она нечётная, т.е.

Ф(-x) = Ф(x)