Методы векторной opt 1-го класса
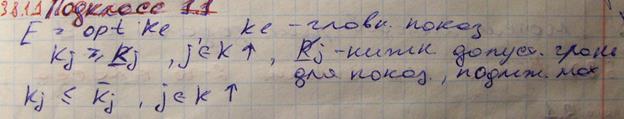
Методика поиска лучшей альтернативы на основе принципа Кондорсе
5 альтернатив, 5 этапов
1. Эксперты ранжируют альтернативы
| Э1 | Э2 | Э3 | Э4 | Э5 |
| а1 а3 а2 а5 а4 | а1 а2 а4 а3 а5 | а1 а2 а5 а3 а4 | а2 а3 а1 а5 а4 | а2 а4 а3 а5 а1 |
| mik | a1 | a2 | a3 | a4 | a5 |
| a1 | - | ||||
| a2 | - | ||||
| a3 | - | ||||
| a4 | - | ||||
| a5 | - |
2. Формируется матрица парных сравнений(5х5) – в скольких случаях было предпочтений i-й альтернативы над k-й
3. Согласно принципу Кондорсе выбирается наилучшая альтернатива. Наилучшей является альтернатива аi, если mik≥mki для всех к не равных i (элементы строки должны превосходить все элементы столбца). К = 4, m14≥m41 , 4>1 — выполняется, т.е. правилу Кондорсе удовлетворяет только альтернатива a1.а1 – наилучшая
Модифицированный алгоритм Кемени-Снелла
У нас есть несколько архитектур вычислительных сетей ( в конспекте их рисунки, они не важны). Все варианты структур оценивались по 4 показателям: К1-надежность, К2-производительность, К3-гибкость и возможность развития, К4-простота реализации.
Отличия метода:
1) Привлекается 1 эксперт
2) Учитывается СП ЛПР
w1=0,375; w2=0,33; w3=0,25; w4=0,042;
Рассмотрим 7 архитектур. Этапы:
1) Производится независимое ранжирование альтернатив по каждому показателю
2)На основе матрицы бинарных предпочтений формируются матрицы с оценками.
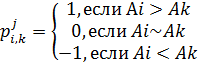
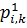 | A1 | A3 | A5 | A6 | A7 | A11 | A13 |
| A1 | - | ||||||
| A3 | -1 | - | |||||
| A5 | -1 | -1 | - | -1 | |||
| A6 | -1 | -1 | -1 | - | -1 | -1 | |
| A7 | -1 | -1 | -1 | - | -1 | ||
| A11 | -1 | -1 | -1 | -1 | -1 | - | -1 |
| A13 | -1 | -1 | - |
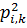 | A1 | A3 | A5 |
| A1 | - | ||
| A3 | - | ||
| A5 | -1 | -1 | - |
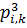 | A1 | A3 | A5 |
| A1 | - | -1 | |
| A3 | - | -1 | |
| A5 | - |
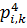 | A1 | A3 | A5 |
| A1 | - | ||
| A3 | - | ||
| A5 | -1 | -1 | - |
3) Определяется м-ца потерь с оценками.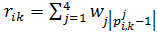 
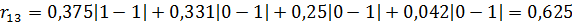
Матрица потерь обрабатывается в несколько циклов. В каждом цикле суммируются строки. Альтернатива с меньшей суммой ставится на 1 место. Соответствующие ей строка и столбец удаляются из матрицы. Переходим к следующему циклу.( A1,A3,A13,A7,A5,A6,A11)
| Nцикла Ai | |||||||
| A1 | 3,545 | ||||||
| A3 | 4,295 | 2,02 | |||||
| A5 | 4,58 | 3,168 | 1,75 | 1,168 | |||
| A6 | 7,66 | 6,25 | 4,83 | 3,42 | 1,5 | 0,084 | |
| A7 | 9,83 | 4,416 | 1,584 | ||||
| A11 | 9,5 | 7,08 | 6,66 | 5,25 | 3,33 | 1,916 | 1,916 |
| A13 | 5,168 | 3,75 | 2,33 |
4) Начиная с конца, рассмотри пары альтернатив. Если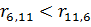 
– альтернативы остаются на своих местах, иначе – меняются местами
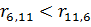;0,084<1,96 => A11 остается на месте; 
; 
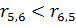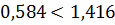, A6 остается на месте; 
; 
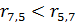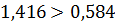=> меняем местами и т.д.
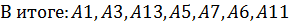
Методика сравнительной оценки 2-ух стр-р по степени доминирования
Методика служит для выбора рациональной структуры из 2-х конкурирующих структур на основе матрицы векторных оценок [Kji]. Операции:
1) Конкурирующие структуры получают название: базовое и новое.
2) Методом экспертных оценок определяются веса частных показат. Vj, j=1..m
3) По каждому частному показателю Kj определяется степень доминирования новой структуры над базовой.
4) Вычисляется обобщенная оценка степени доминирования новой структуры над базовой.
5) Исходя из обобщенной оценки выбирается рациональная структура.
| Ki | Напр. экстрем. | Sб | Sн | |||
| K1 — масса K2 — объем K3 — стоимость K4 — память K5 — гибкость K6 — комфортность | ↓ ↓ ↓ ↑ ↑ ↑ | 0.04 Отл(0.9) Уд(0.5) | 0.08 Уд(0.5) Отл(0.9) | |||
| Ki | Vj | Степень доминир. Sн над Sб | Структ. Оценка с учетом Vj | |||
| K1 K2 K3 K4 K5 K6 | 2↑ 2↓ 2↓ 1,3↑ 1,8↓ 1,8↑ | (2↑)2 (2↓)2 (2↓)1 (1.3↑)3 (1.8↓)3 (1.8↑)4 | ||||
Обобщенная оценка степени доминирования S2 над S1: 22⋅1,33⋅1,84/(22⋅21⋅1,83) >1
Если дробь >1, значит новая превосходит базовую (и наоборот)