Тригонометрическая подстановка

Теорема: Интеграл вида подстановкой или

сводится к интегралу от рациональной функции относительно sint или cost.

Пример:

Теорема: Интеграл вида подстановкой или сводится к интегралу от рациональной функции относительно sint и cost. Теорема: Интеграл вида подстановкой или сводится к интегралу от рациональной функции относительно sint или cost.

2…… Однородные уравнения.

Определение. Функция f(x, y) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество:

Пример. Является ли однородной функция

Таким образом, функция f(x, y) является однородной 3- го порядка.

Определение. Дифференциальное уравнение вида называется однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.

Любое уравнение вида является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения.

Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.

Рассмотрим однородное уравнение

Т.к. функция f(x, y) – однородная нулевого измерения, то можно записать:

Т.к. параметр t вообще говоря произвольный, предположим, что . Получаем:

Правая часть полученного равенства зависит фактически только от одного аргумента 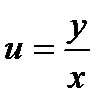, т.е.

Исходное дифференциальное уравнение таким образом можно записать в виде:

Далее заменяем y = ux, .

таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.

Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.

№12. 1…. Определение: Биноминальным дифференциаломназывается выражение

x^m(a + bxⁿ)^pdx

где m, n, и p – рациональные числа.

Как было доказано академиком Чебышевым П.Л. (1821-1894), интеграл от биноминального дифференциала может быть выражен через элементарные функции только в следующих трех случаях:

Если р – целое число, то интеграл рационализируется с помощью подстановки

, где l - общий знаменатель m и n.

Если - целое число, то интеграл рационализируется подстановкой

, где s – знаменатель числа р.

3) Если - целое число, то используется подстановка , где s – знаменатель числа р.

Однако, наибольшее практическое значение имеют интегралы от функций, рациональных относительно аргумента и квадратного корня из квадратного трехчлена.

На рассмотрении этих интегралов остановимся более подробно.

Интегралы вида .

Существует несколько способов интегрирования такого рода функций. В зависимости от вида выражения, стоящего под знаком радикала, предпочтительно применять тот или иной способ.

Как известно, квадратный трехчлен путем выделения полного квадрата может быть приведен к виду:

Таким образом, интеграл приводится к одному из трех типов:

2….. Линейные уравнения.

Определение. Дифференциальное уравнение называется линейным относительно неизвестной функции и ее производной, если оно может быть записано в виде:

при этом, если правая часть Q(x) равна нулю, то такое уравнение называется линейным однороднымдифференциальным уравнением, если правая часть Q(x) не равна нулю, то такое уравнение называется линейным неоднороднымдифференциальным уравнением.

P(x) и Q(x)- функции непрерывные на некотором промежутке a < x < b.

Линейные однородные дифференциальные уравнения.

Рассмотрим методы нахождения общего решения линейного однородного дифференциального уравнения первого порядка вида

.

Для этого типа дифференциальных уравнений разделение переменных не представляет сложностей.

Общее решение:

Линейные неоднородные дифференциальные уравнения.

Для интегрирования линейных неоднородных уравнений (Q(x)¹0) применяются в основном два метода: метод Бернулли и метод Лагранжа.

№13.1… Интегрирование некоторых тригонометрических

функций.

Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.

Интеграл вида .

Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.

Интегралы этого вида вычисляются с помощью подстановки . Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.

,

Тогда

Таким образом: Описанное выше преобразование называется универсальной тригонометрической подстановкой.

Интеграл вида если

функция R является нечетной относительно cosx.

Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.

Функция может содержать cosx только в четных степенях, а следовательно, может быть преобразована в рациональную функцию относительно sinx.

Интеграл вида если

функция R является нечетной относительно sinx.

По аналогии с рассмотренным выше случаем делается подстановка t = cosx.

Тогда

2…. Определение. Дифференциальное уравнение первого порядка вида:

называется уравнением в полных дифференциалах, если левая часть этого уравнения представляет собой полный дифференциал некоторой функции

Интегрирование такого уравнения сводится к нахождению функции u, после чего решение легко находится в виде:

Таким образом, для решения надо определить:

1) в каком случае левая часть уравнения представляет собой полный дифференциал функции u;

2) как найти эту функцию.

Если дифференциальная форма является полным дифференциалом некоторой функции u, то можно записать:

Т.е. .

Найдем смешанные производные второго порядка, продифференцировав первое уравнение по у, а второе – по х:

Приравнивая левые части уравнений, получаем необходимое и достаточное условие того, что левая часть дифференциального уравнения является полным дифференциалом. Это условие также называется условием тотальности.

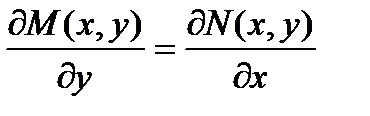
Теперь рассмотрим вопрос о нахождении собственно функции u.

Проинтегрируем равенство :

Вследствие интегрирования получаем не постоянную величину С, а некоторую функцию С(у), т.к. при интегрировании переменная у полагается постоянным параметром.

Определим функцию С(у).

Продифференцируем полученное равенство по у.

Откуда получаем:

№14.1….2) В каждом частичном промежутке [xk, xk+1] выберем по точке ξk и вычислим f(ξk).

Умножим f(ξk) на дли

ну (xk+1 - xk) соответствующего промежутка [xk, xk+1].

4) Сложим все найденные произведения. Сумму

будем называть интегральной суммой.

5) Будем изменять произведённое дробление [a, b] так, чтобы величина λ стремилась к нулю.

Если при этом существует конечный предел

(4) не зависящий от выбора точек ξk, то этот предел называется определенным интегралом от функции f(x) по промежутку [a, b] и обозначается через

Точный смысл соотношения (4) таков: всякому ε > 0 отвечает такое δ > 0, что при любом способе дробления, у которого λ < δ, будет | σ - I | < ε, как бы при этом ни были выбраны точки .

Предельное соотношение (4) имеет довольно своеобразный характер.

Отдадим себе отчет в том, для каких функций введенное понятие оказывается достаточно естественным.

Если у функции f(x) существует интеграл (в этом случае говорят, что f(x) интегрируема), то это означает, что суммы σ, отвечающие дроблениям с достаточно малым λ, будут близки к некоторому постоянному числу, как бы ни выбирать точки ξk. Поэтому, меняя точки ξk, не будем существенно изменять величины суммы σ. Но это возможно лишь за счет того, что изменение точек ξk не вызывает заметного изменения чисел f(ξk) (по крайней мере в большинстве слагаемых суммы σ). Для функций непрерывных указанное обстоятельство и в самом деле имеет место, т. к. точки ξk могут изменяться лишь в коротких промежутках [xk, xk+1], а у непрерывных функций близким значениям аргумента отвечают близкие же значения функции. Поэтому естественно ожидать, что у непрерывной функции определенный интеграл существует. Если же функция f(x) разрывна, то, вообще говоря, нет оснований ожидать у нее существования интеграла.

2.

№15.1…. Сопоставляя доказанную теорему с решением задачи III, видим, что криволинейная трапеция, рассмотренная в упомянутой задаче, имеет площадь F, причем эта площадь выражается формулой Читая эту формулу справа налево, находим Геометрический смысл определенного интеграла. Если f(x) непрерывна и положительна на [a, b], то интеграл представляет собой площадь криволинейной трапеции, ограниченной линиями y = 0, x = a, x = b, y = f(x)

Не следует думать, что условие непрерывности функции необходимо для того, чтобы у нее существовал определенный интеграл. Интеграл может существовать и у разрывной функции. Пусть, например, функция f(x), заданная на промежутке [a, b], равна нулю во всех точках этого промежутка, кроме конечного числа точек z1, z2, ..., zN. Составим для f(x) интегральную сумму σ.

Пусть из точек ξ0, ξ1, ..., ξn-1, входящих в определение σ, p точек совпадают с точками zi, а остальные отличны от них. Тогда в сумме σ будет лишь p слагаемых, отличных от нуля. Если наибольшее из чисел | f(zi) | (i = 1, 2, ..., N) есть K, то, очевидно, | σ | ≤ Kpλ ≤ KNλ, откуда ясно, что при λ → 0 будет и σ → 0. Таким образом, интеграл существует и равен нулю. Приведем теперь пример функции, не имеющей интеграла. Пусть φ(x) задана на промежутке [0, 1] так: Если мы, составляя сумму σ, за точки ξk выберем числа иррациональные, то окажется σ = 0. Если же все ξk взять рациональными, то получится σ = 1. Таким образом, за счет одного лишь уменьшения λ нельзя приблизить σ к какому-либо постоянному числу, и интеграл не существует. В настоящее время известны точные признаки, позволяющие судить, имеет или нет заданная функция определенный интеграл, но мы ограничимся вышеприведенной теоремой об интегрируемости непрерывных функций.

Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами Характеристическое уравнение - корни характеристического уравнения. Общее решение 1. Все корни характеристического уравнения различные, тогда Если среди корней есть пары комплексно-сопряженных корней, например , решение можно записать в виде2. Среди корней характеристического уравнения есть кратные, например, имеет кратность k (остальные - простые), тогда Если среди корней есть пары сопряженных корней кратности k, например , решение можно записать в виде Линейное неоднородное уравнение с постоянными коэффициентами Общее решение неоднородного уравнения есть сумма общего решения однородного уравнения и некоторого частного решения неоднородного уравнения.

№16.1.. Основные свойства интеграла. Установим ряд важных свойств определенного интеграла. Большая часть этих свойств присуща интегралам от любых интегрируемых функций, но мы будем формулировать их для функций непрерывных. Теорема 1. Если f(x) и g(x) - две непрерывные функции, заданные на промежутке [a, b], тот. е. интеграл суммы равен сумме интегралов слагаемых. В самом деле, составляя интегральную сумму для функции f(x) + g(x), очевидно, будем иметь после чего остается перейти к пределу при λ → 0. Аналогично доказывается Теорема 2. Если f(x) - непрерывная функция, а c - постоянное число, то т. е. постоянный множитель можно выносить за знак интеграла. Теорема 3. Пусть f(x) непрерывна на промежутке [a, b]. Если этот промежуток точкой c разложен на части [a, c] и [c, b], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е. В самом деле, будем при раздроблении промежутка [a, b] на части включать c в число точек деления. Если c = xm, то Каждая из написанных здесь трех сумм является интегральной суммой соответственно для промежутков [a, b], [a, c] и [c, b]. Остается перейти к пределу при λ → 0.

2… Линейное неоднородное уравнение второго порядка с постоянными коэффициентами Общее решение неоднородного уравнения есть сумма общего решения однородного уравнения и некоторого частного решения неоднородного. Вид частного решения неоднородного уравнения в некоторых конкретных случаях 1. - многочлен степени m: а) число 0 не является корнем характеристического уравнения , т. е. , тогда где - многочлен порядка m; б) число 0 - корень характеристического уравнения, т. е. b = 0, тогда если 0 - простой корень, т. е. ; если 0 - кратный корень, т. е. a = 0.

№17.1…. Формула Ньютона-Лейбница (формула двойной подстановки) (f непрерывна; F - первообразная для f). Теорема Барроу Если f непрерывна, то Свойства интеграла Линейность Аддитивность Монотонность Если и a < b, то В частности, если то о есть не имеет никакого значения, какая буква (\textstyle x или \textstyle u) стоит под знаком \textstyle f в определенном интеграле по отрезку \left [ a,b \right ]. Зададим произвольное значение \textstyle x \in \left [ a,b \right ] и определим новую функцию \textstyle F(x) = \int\limits_a^x f(t) \,dt. Она определена для всех значений \textstyle x \in \left [ a,b \right ], потому что мы знаем, что если существует интеграл от \textstyle f на \left [ a,b \right ], то существует также интеграл от \textstyle f на \left [ a,x \right ], где a \leqslant x \leqslant b. Напомним, что мы считаем по определению F(a) = \int\limits_a^a f(t)\,dt = 0 (1) Заметим, что F(b) = \int\limits_a^b f(t)\,dt Покажем, что \textstyle F непрерывна на отрезке \left [ a,x \right ]. В самом деле, пусть x, x + h \in \left [ a,x \right ]; тогда F(x + h) - F (x) = \int\limits_a^{(x+h)} f(t)\,dt - \int\limits_a^x f(t)\,dt = \int\limits_x^{(x+h)} f(t)\,dt и если K = sup

2… Комплексная плоскость — это двухмерное вещественное пространство , которое изоморфно полю комплексных чисел . Каждая точка такого пространства — это упорядоченная пара вида (x,y), где x и y — вещественные числа, и где первый элемент пары соответствует вещественной части, а второй элемент пары соответствует мнимой части комплексного числа z = x + iy: Упорядоченную пару (x,y) естественно интерпретировать как радиус-вектор с началом в нуле и с концом в точке (x,y). В силу изоморфизма между и , алгебраические операции над комплексными числами переносятся на операции над соответствующими им радиус-векторами: сложение комплексных чисел — это сложение соответствующих радиус-векторов; умножение комплексных чисел — это преобразование радиус-вектора, связанное с его поворотом и растяжением. Результатом компактификации комплексной плоскости является расширенная комплексная плоскость — комплексная плоскость, дополненная бесконечно удалённой точкой, изоморфная комплексной сфере. Комплексная плоскость связана с комплексной сферой, например, стереографической проекцией. Комплекснозначные функции комплексного переменного обычно интерпретируются как отображения комплексных плоскости или сферы в себя. Поскольку прямые на плоскости (при стереографической проекции) переходят в окружности на сфере, содержащие бесконечно удалённую точку, комплексные функции удобнее рассматривать на сфере. Рассматривая на комплексной плоскости топологию , можно вводить понятия открытых, замкнутых множеств, и давать определения таким объектам как кривые и формулировать такие свойства комплексных функций как непрерывность, дифференцируемость и аналитичность, а комплексное представление позволяет компактно описывать эти свойства на языке соотношений между вещественными и мнимыми частями, а также, между модулями и аргументами соответствующих комплексных чисел. Особую роль в комплексном анализе играют конформные отображени Предел и непрерывность функции комплексной переменной Число называется пределом функций при и обозначается если для любого найдется такое, что для всех удовлетворяющих неравенству , выполняется неравенство Говорим, что , если для любого R > 0 найдётся такое, что для всех таких, что , выполняется неравенство Следует иметь в виду, что для данной функции существование предела по любому фиксированному пути () ещё не гарантирует существование предела при . Пример 1 Пусть Показать, что не существует Для предела при по любому лучу имеем т. е. эти пределы различны для различных направлений - они запол-няют сплошь отрезок [-1, 1], и, следовательно, не существует Функция называется непрерывной в точке если она определена в этой точке и Функция , непрерывная в каждой точке области D, называется непрерывной в этой области. Функция называется равномерно непрерывной в области D, если для любого найдется такое, что для любых точек и из области D таких, что , выполняется неравенство

18.1 Замена переменной в определенном интеграле Определенный интеграл по переменной x можно преобразовать в определенный интеграл относительно переменной t с помощью подстановки x = g (t): Новые пределы интегрирования по переменной t определяются выражениями где g -1 - обратная функция к g, т.е. t = g -1(x). Интегрирование по частям для определенного интеграла В этом случае формула интегрирования по частям имеет вид: где означает разность значений произведения функций uv при x = b и x = a Пересчитаем пределы интегрирования. Если x = 0, то t = −1. Если же x = 1, то t = 2. Тогда интеграл через новую переменную t легко вычисляется:

2…. Рассмотрим функцию комплексной переменной , определенную на некоторой области и имеющую в какой – либо точке этой области производную

Стремление к нулю Dz®0 может осуществляться в следующих случаях:

1)

2)

В первом случае:

Во втором случае:

Тогда должны выполняться равенства:

Эти равенства называются условиями Коши – Римана, хотя еще раньше они были получены Эйлером и Даламбером.

Теорема. Если функция имеет производную в точке

z = x + iy, то ее действительные компоненты u и v имеют в точке (х, у) частные производные первого порядка, удовлетворяющие условию Коши – Римана.

Также справедлива и обратная теорема.

На основании этих теорем можно сделать вывод, что из существования производной следует непрерывность функции.

Теорема. Для того, чтобы функция была аналитической на некоторой области необходимо и достаточно, чтобы частные производные первого прядка функций u и v были непрерывны на этой области и выполнялись условия Коши – Римана.

№19.1… Формула интегрирования по частям в определенном интегралеТЕОРЕМА. Пусть функции u=u(x) и v=v(x) имеют непрерывные производные на отрезке [а,b]. Тогда где Формула (4) называется формулой интегрирования по частям для определенного интеграла.

Пример 22. Вычислить Пусть u=ln(1+x),dv=dx Тогда du=d(ln(1+x))=(ln(1+x))'dx= и v=∫dv=∫dx=x. Применяя (4), получаем Для нахождения полученного интеграла положим 1+х=t. Тогда dx=dt, x=t-1 и если х=0, то t=1, если x=1, то t=2. Следовательно, Определение 1: Кривая Г называется гладкой ,если она имеет непрерывно изменяющуюся касательную. Определение 2: Кривая называется кусочно-гладкой ,если она состоит из конечного числа гладких дуг. Основные свойства : Пусть на комплексной плоскости Z задана кусочно-гладкая кривая С длиной l, используя параметрическое задание кривой С зададим h(t) и x (t), где h и x являются кусочно-гладкими кривыми от действительной переменной t. Пусть a<= t<=b, причем a и b могут быть бесконечными числами . Пусть x и h удовлетворяют условию : [x‘(t)]2 + [h‘(t)]2 ¹ 0. Очевидно, что задание координат h =h(t) и x=x (t), равносильно заданию комплексной функции z (t)= x (t) + ih(t). Пусть в каждой точке z (t) кривой С определена некоторая функция f (z ). Разобьем кривую С на n – частичных дуг точками деления z0 , z1 , z2 , …, z n-1 соответствующие возрастающим значениям параметра t, т.е. t0, t1, …, t i+1 > t i. Dz i =z i – z i-1. Составим интегрируемую функцию S = åf (z*)Dz i . где z*– производная точки этой дуги. Если при стремлении max |Dz i |® 0 существует предел частных сумм не зависящий ни от способа разбиения кривой С на частичные дуги, ни от выбора точек z i , то этот предел называется интегралом от функции f (z ) по кривой С. f (zi* ) = u (Pi*) + iv (Pi*) где Dz i = Dx (t) + iDh(t) (x (t) и h(t) - действительные числа) Очевидно, что (4) состоит из суммы двух частных сумм, криволинейных интегралов действительной переменной. Переходя в (4) к пределу при Dx и Dh ® 0 и предполагая, что данные пределы существуют, получаем : Заметим, что для существования криволинейного интегралов, входящих в (5), а тем самым и для существования интеграла (2) достаточно кусочной непрерывности функций u и v. Это означает, что (2) существует и в случае неаналитичности функции f (z ).

2… Интеграл существует и является функцией комплексной переменной. Справедлива формула :Эта формула устанавливает возможность вычисления производной от исходного интеграла путем дифференцирования подинтегральной функции по параметру. ТЕОРЕМА. Пусть f(Z) является аналитической функцией в области G и непрерывной в области G (G включая граничные точки ), тогда во внутренних точках области G существует производная любого порядка от функции f(Z) причем для ее вычисления имеет место формула : С помощью формулы (3) можно получить производную любого порядка от аналитической функции f (Z) в любой точке Z области ее аналитичности. Для доказательства этой теоремы используется формула (2) и соответственные рассуждения, которые привели к ее выводу.

20.1.. Пусть требуется найти значение какой-либо геометрической или физической величины А (площадь фигуры, объем тела, давление жидкости на вертикальную пластину и т. д.), связанной с отрезком [a;b] изменения независимой переменной х. Предполагается, что эта величина А аддитивна, т. е. такая, что при разбиении отрезка [а; b] точкой с є (а; b) на части [а; с] и [с; b] значение величины А, соответствующее всему отрезку [а; b], равно сумме ее значений, соответствующих [а; с] и [с; b]. Для нахождения этой величины А можно руководствоваться одной из двух схем: I схема (или метод интегральных сумм) и II схема (или метод дифференциала). Первая схема базируется на определении определенного интеграла. 1. Точками х0 = а, x1,..., xn = b разбить отрезок [а;b] на n частей. В соответствии с этим, интересующая нас величина А разобьется на n «элементарных слагаемых» ΔAi (i = 1,...,n): А = ΔA1+ΔА2 +...+ ΔАn. 2. Представить каждое «элементарное слагаемое» в виде произведения некоторой функции (определяемой из условия задачи), вычисленной в произвольной точке соответствующего отрезка на его длину: ΔAi ≈ ƒ(ci)Δxi. При нахождении приближенного значения ΔАi допустимы некоторые упрощения: дугу на малом участке можно заменить хордой, стягивающей ее концы; переменную скорость на малом участке можно приближенно считать постоянной и т. д. Получим приближенное значение величины А в виде интегральной суммы: . Искомая величина А равна пределу интегральной суммы, т. е. Указанный «метод сумм», как видим, основан на представлении интеграла как о сумме бесконечно большого числа бесконечно малых слагаемых. Схема I была применена для выяснения геометрического и физического смысла определенного интеграла. Вторая схема представляет собой несколько видоизмененную схему I и называется «метод дифференциала» или «метод отбрасывания бесконечно малых высших порядков»: 1) на отрезке [а;b] выбираем произвольное значение х и рассматриваем переменный отрезок [а; х]. На этом отрезке величина А становится функцией х: А = А(х), т. е. считаем, что часть искомой величины А есть неизвестная функция А(х), где х є [a;b] — один из параметров величины А; 2) находим главную часть приращения ΔА при изменении х на малую величину Δх = dx, т. е. находим дифференциал dA функции А = А(х): dA = ƒ(х) dx, где ƒ(х), определяемая из условия задачи, функция переменной х (здесь также возможны различные упрощения); 3) считая, что dA ≈ ΔА при Δх → 0, находим искомую величину путем интегрирования dA в пределах от а до b:

2.. числовой ряд с комплексными членами Числовые ряды.Определение 1: Числовым рядом называется Определение 2: Числовой ряд называется сходящимся, если последовательность частичных сумм этого ряда: конечна. Суммой числового ряда в этом случае называется предел Если предел не существует либо бесконечен, то ряд расходится. 1. Линейность. Если ряды и сходятся (и их суммы соответственно равны и ), то линейная комбинация тоже сходится (к сумме ). Это свойство вытекает из линейности предела 2. На сходимость ряда не влияет изменение первых членов ряда: и сходятся или расходятся одновременно, если при (конечно, суммы, в которые сходятся ряды разные). Дело в том, что частичные суммы при этих рядов отличаются на постоянную величину: (при ). Следовательно, если имеет предел, то и имеет его (и наоборот).

21.1… Пусть требуется найти значение какой-либо геометрической или физической величины А (площадь фигуры, объем тела, давление жидкости на вертикальную пластину и т. д.), связанной с отрезком [a;b] изменения независимой переменной х. Предполагается, что эта величина А аддитивна, т. е. такая, что при разбиении отрезка [а; b] точкой с є (а; b) на части [а; с] и [с; b] значение величины А, соответствующее всему отрезку [а; b], равно сумме ее значений, соответствующих [а; с] и [с; b]. Для нахождения этой величины А можно руководствоваться одной из двух схем: I схема (или метод интегральных сумм) и II схема (или метод дифференциала). Первая схема базируется на определении определенного интеграла. 1. Точками х0 = а, x1,..., xn = b разбить отрезок [а;b] на n частей. В соответствии с этим, интересующая нас величина А разобьется на n «элементарных слагаемых» ΔAi (i = 1,...,n): А = ΔA1+ΔА2 +...+ ΔАn. 2. Представить каждое «элементарное слагаемое» в виде произведения некоторой функции (определяемой из условия задачи), вычисленной в произвольной точке соответствующего отрезка на его длину: ΔAi ≈ ƒ(ci)Δxi. При нахождении приближенного значения ΔАi допустимы некоторые упрощения: дугу на малом участке можно заменить хордой, стягивающей ее концы; переменную скорость на малом участке можно приближенно считать постоянной и т. д. Получим приближенное значение величины А в виде интегральной суммы: . Искомая величина А равна пределу интегральной суммы, т. е. Указанный «метод сумм», как видим, основан на представлении интеграла как о сумме бесконечно большого числа бесконечно малых слагаемых. Схема I была применена для выяснения геометрического и физического смысла определенного интеграла. Вторая схема представляет собой несколько видоизмененную схему I и называется «метод дифференциала» или «метод отбрасывания бесконечно малых высших порядков»: 1) на отрезке [а;b] выбираем произвольное значение х и рассматриваем переменный отрезок [а; х]. На этом отрезке величина А становится функцией х: А = А(х), т. е. считаем, что часть искомой величины А есть неизвестная функция А(х), где х є [a;b] — один из параметров величины А; 2) находим главную часть приращения ΔА при изменении х на малую величину Δх = dx, т. е. находим дифференциал dA функции А = А(х): dA = ƒ(х) dx, где ƒ(х), определяемая из условия задачи, функция переменной х (здесь также возможны различные упрощения); 3) считая, что dA ≈ ΔА при Δх → 0, находим искомую величину путем интегрирования dA в пределах от а до b:

2… Размещениями из n элементов по k называются соединения, которые можно образовать из n элементов, собирая в каждое соединение по k элементов, при этом соединения могут отличаться друг от друга как самими элементами, так и порядком их расположения. Например, из 3 элементов (abc) по 2 можно образовать следующие размещения: ab,ac,ba,bc,ca,cb. Число всех возможностей размещений, которые можно образовать из n элементов по k, обозначается символом и вычисляется по формуле: . Перестановками из n элементов называются соединения, каждое из которых содержит все n элементов, отличающихся поэтому друг от друга только порядком расположения элементов. Число всех возможных перестановок, которые можно образовать из n элементов, обозначаться символом P_n: P_n=1*2*3*….n=n!

Сочетаниями из n элементов по k называются соединения, которые можно образовать из n элементов, собирая в каждое соединение k элементов; при этом соединения отличаются друг от друга только самими элементами (различие порядка их расположения во внимание не принимается)

22.1…. Площадь криволинейной трапеции, расположенной «выше» оси абсцисса (f(x)>=0), равна соответствующему определенному интегралу Отметим, что если криволинейная трапеция расположена «ниже» оси Ох (х)<0), то ее площадь может быть найдена по формуле. . Площадь фигуры ограниченная кривыми, находится по формуле: . Если криволинейная трапеция ограниченна кривой, заданной параметрический находится по формуле

2… некоторые задачи теории графов: 1. Проблема семи мостов Кёнигсберга – один из первых результатов в теории графов. 2. Проблема четырех красок 3. Задача коммивояжера 4. Задача о клике5 нахождение минимального стягивающего дерев. И т д.

№23.1 рассмотрим

2… Граф это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Графы обычно изображаются в виде геометрических фигур, так что вершины графа изображаются точками

№24.1… Если j(х) – непрерывная положительная функция, убывающая на промежутке [1;¥), то ряд j(1) + j(2) + …+ j(n) + … = и несобственный интеграл одинаковы в смысле сходимости.

Пример. Ряд сходится при a>1 и расходится a£1 т.к. соответствующий несобственный интеграл сходится при a>1 и расходится a£1. Ряд называется общегармоническимрядом.

Следствие. Если f(x) и j(х) – непрерывные функции на интервале (a, b] и то интегралы и ведут себя одинаково в смысле сходимости.

2…. Граф это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек. Вершины прилегающие к одному и тому же ребру, называютя смежными. Если ребра ориентированные, что обычно показывают стрелками, то они называются дугами, и граф с такими ребрами называются ориентированным графом. Если ребра не имеют ориентации, граф называется неориентированным.

№25.ё1… Определение. Сумма членов бесконечной числовой последовательности называется числовым рядом.

При этом числа будем называть членами ряда, а u_n – общим членом ряда.

Определение. Суммы , n = 1, 2, … называются частными (частичными) суммамиряда.

Таким образом, возможно рассматривать последовательности частичных сумм ряда S₁, S₂, …,S_n, …

Определение. Ряд называется сходящимся, если сходится последовательность его частных сумм. Сумма сходящегося ряда – предел последовательности его частных сумм.