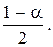Проверка статистической гипотезы о математическом ожидании нормального распределения при известной дисперсии
Пусть имеется нормально распределенная случайная величина x,, определенная на множестве объектов некоторой генеральной совокупности. Известно, что Dx = s 2. Математическое ожидание Mx неизвестно. Допустим, что имеются основания предполагать, что Mx = a, где a – некоторое число (такими основаниями могут быть ограниченные сведения об объектах генеральной совокупности, опыт исследования подобных совокупностей и т. д.). Будем считать также, что имеется другая информация, указывающая на то, что Mx = a1, где a1 > a.
I. Выдвигаем нулевую гипотезу H0: Mx = a;
при конкурирующей гипотезе H1: Mx = a1.
Делаем выборку объема n: x1, x2,..., xn . В основе проверки лежит тот факт, что случайная величина  (выборочная средняя) распределена по нормальному закону с дисперсией s 2/n и математическим ожиданием, равным a в случае справедливости H0, и равным a1 в случае справедливости H1.
(выборочная средняя) распределена по нормальному закону с дисперсией s 2/n и математическим ожиданием, равным a в случае справедливости H0, и равным a1 в случае справедливости H1.
Очевидно, что если величина  оказывается достаточно малой, то это дает основание предпочесть гипотезу H0 гипотезе H1. При достаточно большом значении
оказывается достаточно малой, то это дает основание предпочесть гипотезу H0 гипотезе H1. При достаточно большом значении  более вероятна справедливость гипотезы H1. Задачу можно было бы поставить так: требуется найти некоторое критическое число, которое разбивало бы все возможные значения выборочной средней ( в условиях данной задачи это все действительные числа ) на два полубесконечных промежутка. При попадании
более вероятна справедливость гипотезы H1. Задачу можно было бы поставить так: требуется найти некоторое критическое число, которое разбивало бы все возможные значения выборочной средней ( в условиях данной задачи это все действительные числа ) на два полубесконечных промежутка. При попадании 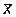 в левый промежуток следовало бы принимать гипотезу H0, а при попадании
в левый промежуток следовало бы принимать гипотезу H0, а при попадании 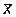 в правый промежуток предпочтение следовало бы оказать гипотезе H1. Однако на самом деле поступают несколько иначе.
в правый промежуток предпочтение следовало бы оказать гипотезе H1. Однако на самом деле поступают несколько иначе.
В качестве статистического критерия выбирается случайная величина
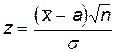 ,
,
распределенная по нормальному закону, причем Mz = 0 и Dz = 1 ( это следует из свойств математического ожидания и дисперсии ) в случае справедливости гипотезы H0. Если справедлива гипотеза H1, то
Mz = a* = ( a1 – a ) 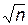 /s, Dz = 1.
/s, Dz = 1.
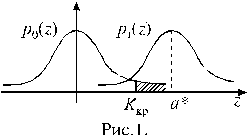 |
На рисунке 1. изображены графики p0(z) и p1(z) – функций плотности распределения случайной величины z при справедливости гипотез H0 и H1, соответственно.
Если величина 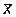 , полученная из выборочных данных, относительно велика, то и величина z велика, что является свидетельством в пользу гипотезы H1. Относительно малые значения
, полученная из выборочных данных, относительно велика, то и величина z велика, что является свидетельством в пользу гипотезы H1. Относительно малые значения 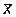 приводят к малым значениям z, что свидетельствует в пользу гипотезы H0. Отсюда следует, что должна быть выбрана правосторонняя критическая область. По принятому уровню значимости a (например a = 0,05), используя то, что случайная величина z распределена по нормальному закону, определим значение Kкр из формулы
приводят к малым значениям z, что свидетельствует в пользу гипотезы H0. Отсюда следует, что должна быть выбрана правосторонняя критическая область. По принятому уровню значимости a (например a = 0,05), используя то, что случайная величина z распределена по нормальному закону, определим значение Kкр из формулы
a = P(Kкр < z <¥) = F(¥) – F(Kкр) = 0,5 – F(Kкр).
Отсюда 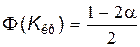 , и осталось воспользоваться таблицей функции Лапласа для нахождения числа Kкр.
, и осталось воспользоваться таблицей функции Лапласа для нахождения числа Kкр.
Если величина z, полученная при выборочном значении 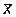 , попадает в область принятия гипотезы (z < Kкр), то гипотеза H0 принимается (делается вывод, что выборочные данные не противоречат гипотезе H0). Если величина z попадает в критическую область, то гипотеза H0 отвергается.
, попадает в область принятия гипотезы (z < Kкр), то гипотеза H0 принимается (делается вывод, что выборочные данные не противоречат гипотезе H0). Если величина z попадает в критическую область, то гипотеза H0 отвергается.
В данной задаче может быть подсчитана мощность критерия:
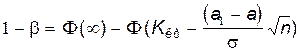
Мощность критерия тем больше, чем больше разность a1– a.
II. Если в предыдущей задаче поставить другое условие:
H0: Mx = a;
H1: Mx = a1 , a1 < a,
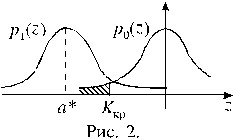 |
то, сохранив смысл всех рассуждений, здесь придется рассматривать левостороннюю критическую область, как изображено на рисунке 2. Здесь, как и в предыдущем случае,
a* = ( a1 – a ) 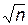 /s, а величина Kкр определяется из формулы
/s, а величина Kкр определяется из формулы
a = P(–¥ < z < Kкр) = F( Kкр) –F(–¥) = F( Kкр) + 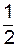 .
.
Используя формулу –F( Kкр) = F( –Kкр), получаем:
F( –Kкр) = 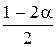 .
.
Отметим, что по смыслу задачи здесь Kкр – отрицательное число.
Значения z, вычисленные по выборочным данным, превышающие Kкр, согласуются с гипотезой H0. Если величина z попадает в критическую область (z < Kкр), то гипотезу H0 следует отвергнуть, считая предпочтительной гипотезу H1.
III. Рассмотрим теперь такую задачу:
H0: Mx = a;
H1: Mx ¹ a.
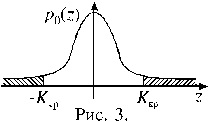 |
В данном случае большие отклонения величины z от нуля в положительную или отрицательную сторону должны приводить к заключению о ложности гипотезы H0, то есть здесь следует рассматривать двустороннюю критическую область, как изображено на рисунке 3.
Критическое значение Kкр определяется с помощью соотношения
P(–Kкр < z < Kкр) = 1 – a = F( Kкр) –F( – Kкр) = 2F( Kкр) .
Из этого соотношения следует:
F( Kкр) =