Распределение рекламного бюджета
Фирма рекламирует свою продукцию с использованием четырех средств: телевидения, радио, газет и афиш. Из различных рекламных экспериментов, которые проводились в прошлом, известно, что эти средства приводят к увеличению прибыли соответственно на 10, 3, 7 и 4 у.е. в расчете на 1 у.е., затраченную на рекламу.
Распределение рекламного бюджета по различным средствам подчинено следующим ограничениям:
а) полный бюджет не должен превосходить 500 000 у.е.;
б) следует расходовать не более 40 % бюджета на телевидение и не более 20 % бюджета на афиши;
в) вследствие привлекательности для подростков радио на него следует расходовать по крайней мере половину того, что планируется на телевидение.
Сформулируйте задачу распределения средств по различным источникам как задачу линейного программирования и решите ее.
Задача об оптимальном использовании ограниченных ресурсов
Небольшая фирма производит два вида продукции: столы и стулья. Для изготовления одного стула требуется 3 м древесины, а для изготовления одного стола – 7 м. На изготовление одного стула уходит 2 часа рабочего времени, а на изготовление стола – 8 часов. Каждый стул приносит 1 ден. ед. прибыли, а каждый стол - 3 ден. ед. Сколько стульев и сколько столов должна изготовить эта фирма для получения максимальной прибыли, если она рас-полагает 20 м древесины и 400 часами рабочего времени?
Задача 5.
Провести моделирование и решить специальную задачу линейного программирования.
Транспортная задача
Компания, занимающаяся ремонтом автомобильных дорог, в следующем месяце будет проводить ремонтные работы на пяти участках автодорог. Песок на участки ремонтных работ может доставляться из трех карьеров, месячные объемы предложений по карьерам известны. Из планов производства ремонтных работ известны месячные объемы потребностей по участкам работ. Имеются экономические оценки транспортных затрат (в у.е.) на перевозку 1тонны песка с карьеров на ремонтные участки.
Числовые данные для решения содержатся ниже в матрице планирования
Требуется:
1) Предложить план перевозок песка на участки ремонта автодорог, который обеспечивает минимальные совокупные транспортные издержки.
2) Что произойдет с оптимальным планом, если изменятся условия перевозок: а) появится запрет на перевозки от первого карьера до второго участка работ?; б) по этой коммуникации будет ограничен объем перевозок 3 тоннами?
Матрица планирования:
 Участки работ Карьеры Участки работ Карьеры | В1 | В2 | В3 | В4 | В5 | Предложение |
| А1 | ||||||
| А2 | ||||||
| А3 | ||||||
| Потребности |  15 15 |
Задача о назначениях
В распоряжении некоторой компании имеется 6 торговых точек и 6 продавцов. Из прошлого опыта известно, что эффективность работы продавцов в различных торговых точках неодинакова. Коммерческий директор компании произвел оценку деятельности каждого продавца в каждой торговой точке. Результаты этой оценки представлены в таблице
| Продавец | Объемы продаж по торговым точкам, USD/тыс.шт. | |||||
| I | II | III | IV | V | VI | |
| A | - | |||||
| B | ||||||
| C | ||||||
| D | ||||||
| E | ||||||
| F |
(назначение первого продавца на четвертую торговую точку недопустимо по медицинским показаниям, т.е. в матрице объемов продаж проставлен запрет – «-»).
Как коммерческий директор должен осуществить назначение продавцов по торговым точкам, чтобы достичь максимального объема продаж?
Задание 6.
Необходимо решить транспортную задачу: минимизировать расходы на доставку продукции заказчикам со складов фирмы, учитывая следующие затраты на доставку одной единицы продукции, объём заказа и количество продукции, хранящейся на каждом складе. Тарифы на перевозку единицы продукции, объёмы запасов продукции на складах, а также объёмы заказанной продукции представлены в таблице №1.
 Склад Склад | Магазины заказчики | Запасы на складе (ед. прод) | ||||
| “Анна” | “Вада” | “Ева” | “Алла” | “Мех” | ||
| “Таганка” | ||||||
| “ВВЦ” | ||||||
| “Щёлково” | ||||||
| “Коньково” | ||||||
| Объём заказа (ед. прод) |
Примерные задания для компьютерного тестирования по темам 1-5
1.
 | |||
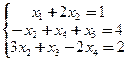 | |||
Какие из приведенных решений являются опорными для следующей системы уравнений:
2. 
Из четырех видов сырья необходимо составить смесь, в состав которой должно входить не менее 26 ед. химического вещества А, 30 ед. - вещества В и 24 ед. - вещества С. Количество единиц химического вещества, содержащегося в 1 кг сырья каждого вида, указано в таблице. В ней же приведена цена 1 кг сырья каждого вида.
| Вещество | Количество единиц вещества, содержащегося в 1 кг сырья вида | |||
| А | - | |||
| В | - | |||
| С | ||||
| Цена 1 кг сырья |
Составить смесь, содержащую не менее нужного количества веществ данного вида и имеющую минимальную стоимость. Какая из математических моделей соответствует данной задаче, указать смысл входящих переменных, единицы измерения.
а) 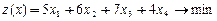 б)
б) 


в) 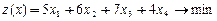 г)
г) 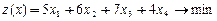

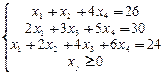
3. В какой точке множества допустимых решений достигается минимум целевой функции  ,
,
 X2 а) в точке А
X2 а) в точке А
C б) в точке В
в) в точке С
B D г) в точке Е
д) в точке Д
3. Определить, какая из задач линейного программирования записана в канонической форме?
а)  б)
б) 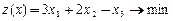
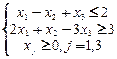

в) 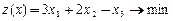
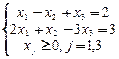
4. Найти опорный план транспортной задачи, заданной следующей таблицей и вычислить соответствующие транспортные издержки.
| Постав-щики | Потребители | Запасы | |||||||||||
| В1 | В2 | В3 | В4 | В5 | |||||||||
| А1 | |||||||||||||
| А2 | |||||||||||||
| А3 | |||||||||||||
| Потреб-ности |
а) z(для опорного плана) = 1390
б) z(для опорного плана) =1380
в) z(для опорного плана) =1360
г) z(для опорного плана) =1340
5. В соответствии с первой геометрической интерпретацией множество допустимых планов задачи линейного программирования всегда представляется в виде:
- замкнутого множества
- многогранного выпуклого множества
- выпуклого многогранника
6. Графический метод решения ЗЛП всегда может быть применен к задачам следующего типа:
- К задачам, у которых число переменных совпадает с числом ограничений
- К каноническим задачам линейного программирования
- К задачам, у которых число переменных равно 2
- К каноническим задачам линейного программирования, у которых число переменных на 2 превосходит числа ограничений
- К задачам, у которых число переменных меньше числа ограничений
7. Выберите верные утверждения
- Если ЗЛП имеет единственное решение, то оно может находиться в граничной точке множества допустимых планов задачи
- Граничные точки множества не могут являться оптимальным решением ЗЛП
- Оптимальное решение ЗЛП в некоторых случаях может находиться внутри области допустимых планов задачи
- Среди предложенных вариантов нет верных
8. При построении двойственной задачи к ЗЛП условия неотрицательности:
- Будут наложены на все двойственные переменные
- Не будут наложены ни на одну из двойственных переменных
- Для того, чтобы ответить на вопрос необходимо анализировать конкретное условие задачи
9. Задача, частично решенная графическим способом:


- Имеет единственное решение
- Имеет бесконечное множество решений
- Не имеет оптимальных решений
- Не имеет допустимых решений
- Точно ответить на вопрос нельзя – не хватает информации
Критерии выставления баллов за контрольную работу №1 в соответствие с балльно-рейтинговой системой приведены в следующей таблице.
| Кол-во баллов | Критерии оценки | Формируемые компетенции |
| 13-15 | Работа выполнена на 85-100%. Студент владеет теоретическим материалом, отсутствуют ошибки при описании теории, формулирует собственные, самостоятельные, обоснованные, аргументированные суждения, представляет полные и развернутые ответы на дополнительные вопросы, демонстрирует сформированность всех компетенций. | ПК-4, ПК-5 |
| 10-12 | Работа выполнена на 70-84%. Студент владеет теоретическим материалом, отсутствуют ошибки при описании теории, формулирует собственные, самостоятельные, обоснованные, аргументированные суждения, допуская незначительные ошибки при ответе на дополнительные вопросы, демонстрирует наличие основных компетенций. | ПК-4, ПК-5 |
| 7-9 | Даны правильные решения на 50-69% Студент владеет теоретическим материалом на минимально допустимом уровне, отсутствуют ошибки при описании теории, испытывает затруднения в формулировке собственных обоснованных и аргументированных суждений, допуская незначительные ошибки при ответе на дополнительные вопросы, демонстрирует некоторое наличие компетенции. | ПК-4, ПК-5 |
| 4-6 | Работа выполнена на 30-49%. Студент не владеет теоретическим материалом, допуская ошибки по сущности рассматриваемых (обсуждаемых) вопросов, испытывает затруднения в формулировке собственных обоснованных и аргументированных суждений, допускает ошибки при ответе на дополнительные вопросы. | ПК-4 |
| 0-3 | Решены правильно менее 30% задач. Студент практически не владеет теоретическим материалом, допуская грубые ошибки, испытывает затруднения в формулировке собственных суждений, неспособен ответить на дополнительные вопросы. | __ |
Критерии выставления баллов за контрольную работу №2 в соответствие с балльно-рейтинговой системой приведены в следующей таблице.
| Кол-во баллов | Критерии оценки | Формируемые компетенции |
| 21-25 | Работа выполнена на 85-100%. Студент владеет теоретическим материалом, отсутствуют ошибки при описании теории, формулирует собственные, самостоятельные, обоснованные, аргументированные суждения, представляет полные и развернутые ответы на дополнительные вопросы, демонстрирует сформированность всех компетенций. | ПК-4, ПК-5 |
| 16-20 | Работа выполнена на 70-84%. Студент владеет теоретическим материалом, отсутствуют ошибки при описании теории, формулирует собственные, самостоятельные, обоснованные, аргументированные суждения, допуская незначительные ошибки при ответе на дополнительные вопросы, демонстрирует наличие основных компетенций. | ПК-4, ПК-5 |
| 11-15 | Даны правильные решения на 50-69% Студент владеет теоретическим материалом на минимально допустимом уровне, отсутствуют ошибки при описании теории, испытывает затруднения в формулировке собственных обоснованных и аргументированных суждений, допуская незначительные ошибки при ответе на дополнительные вопросы, демонстрирует некоторое наличие компетенции. | ПК-4, ПК-5 |
| 6-10 | Работа выполнена на 30-49%. Студент не владеет теоретическим материалом, допуская ошибки по сущности рассматриваемых (обсуждаемых) вопросов, испытывает затруднения в формулировке собственных обоснованных и аргументированных суждений, допускает ошибки при ответе на дополнительные вопросы. | ПК-4 |
| 0-5 | Решены правильно менее 30% задач. Студент практически не владеет теоретическим материалом, допуская грубые ошибки, испытывает затруднения в формулировке собственных суждений, неспособен ответить на дополнительные вопросы. | __ |
Вопросы к экзамену
Перечень вопросов к экзамену
1. Обсуждение основ математического моделирования в экономических исследованиях. Методы математического программирования.
2. Основные понятия линейного программирования. Этапы построения моделей
3. Модель оптимального планирования производства.
4. Модель о смешении. Задача о диете.
5. Модель оптимального раскроя.
6. Модель оптимального планирования финансов.
7. Методика построения задач линейного программирования.
8. Геометрическая интерпретация решение задачи линейного программирования в случае двух переменных.
9. Методика решения задач линейного программирования в случае двух переменных графическим методом
10. Графический анализ чувствительности оптимальности решения.
11. Графический анализ чувствительности ограничений задачи линейного программирования.
12. Графический анализ чувствительности целевой функции задачи линейного программирования.
13. Ключевые идеи симплекс-метода. Канонический вид задачи линейного программирования. Определение базисных решений.
14. Алгоритм симплекс-метода. Условие допустимости решения. Условие оптимальности решения. Метод Гаусса-Жордана вычисления нового базисного решения.
15. Искусственное начальное решение. М-метод.
16. Особые случаи применения симплекс-метода: вырожденность и альтернативные оптимальные решения.
17. Особые случаи применения симплекс-метода: неограниченные решения и отсутствие допустимых решений.
18. Предпосылки к рассмотрению двойственной задачи. Двойственность задач в линейном программировании.
19. Первая теорема двойственности.
20. Вторая теорема двойственности.
21. Нахождение исходного допустимого базисного решения методом северо-западного угла и методом минимального элемента.
22. Метод потенциалов решения транспортной задачи. Понятие цикла.
23. Связь коэффициентов целевой функции через свободные переменные с потенциалами.
24. Признак оптимальности решения транспортной задачи методом потенциалов и аналогия признака оптимальности в симплекс-таблице.
25. Понятие цикла. Метод потенциалов решения транспортной задачи.
26. Целочисленные переменные в задачах экономического планирования. Общая задача целочисленного программирования, общая задача целочисленного ЛП, задача частично-целочисленного программирования.
27. Геометрическая интерпретация задачи целочисленного программирования.
28. Алгоритм Гомори.
29. Метод ветвей и границ.
30. Задача о назначениях.
31. Нелинейное и динамическое программирование.
32. Общая постановка задач конечномерной оптимизации. Выпуклые множества и их свойства. Экономическая и геометрическая интерпретации.
33. Теорема Вейерштрасса и следствие из неё.
34. Метод множителей Лагранжа в гладких экстремальных задачах с ограничениями типа равенств и неравенств.
35. Задачи выпуклого программирования.
36. Теорема Куна-Таккера.
37. Понятие Марковского случайного процесса.
38. Принцип оптимальности Беллмана. Рекуррентные соотношения Беллмана.
39. Модели сетевого планирования.
40. Схемы численных методов оптимизации: градиентный метод с постоянным шагом, метод скорейшего спуска.
41. Схемы численных методов оптимизации: метод Ньютона, метод проекции градиента.
42. Многокритериальная оптимизация. Постановка и методы решения задач многокритериальной оптимизации.
43. Примеры многокритериальных задач в экономике.
44. Задачи систем массового обслуживания. Экономико-математическая постановка задач массового обслуживания.
45. Задачи анализа замкнутых и разомкнутых систем массового обслуживания.
46. Модели систем массового обслуживания в коммерческой деятельности.
47. СМО с отказами. СМО с ожиданием (очередью).
