Параллельными идеально проводящими поверхностями
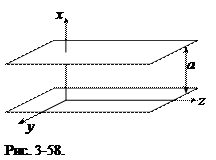 1.Задача – найти характеристики электромагнитного поля, которое существует в диэлектрической среде в пространстве между идеально проводящими поверхностями. Для решения задачи необходимо подробно описать поле в этом пространстве с помощью уравнений Максвелла и решить полученные уравнения с учетом граничных условий. На рис. 3-58 приведены две проводящие плоскости, расстояние между которыми a. Нижняя плоскость имеет координату x = 0, верхняя – координату x = a. Диэлектрическая и магнитная проницаемости среды между плоскостями, соответственно, равны e и m. Диэлектрическая среда, в которой распространяется волна, является непроводящей и нейтральной.
1.Задача – найти характеристики электромагнитного поля, которое существует в диэлектрической среде в пространстве между идеально проводящими поверхностями. Для решения задачи необходимо подробно описать поле в этом пространстве с помощью уравнений Максвелла и решить полученные уравнения с учетом граничных условий. На рис. 3-58 приведены две проводящие плоскости, расстояние между которыми a. Нижняя плоскость имеет координату x = 0, верхняя – координату x = a. Диэлектрическая и магнитная проницаемости среды между плоскостями, соответственно, равны e и m. Диэлектрическая среда, в которой распространяется волна, является непроводящей и нейтральной.
Допустим, волна распространяется в направлении оси z и векторы E и H волны не зависят от координаты y. В этом случае в уравнениях Максвелла для ротора векторов E и H производные по координате y равны нулю. Приняв во внимание, что два вектора равны, если равны их компоненты, запишем уравнения для компонент роторов E и H относительно декартовой системы.
Из уравнения [Ñ, E] = - 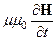 имеем:
имеем:
1) - 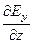 = -
= - 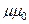
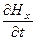 ; 2)
; 2) 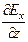 -
- 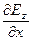 = -
= - 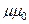
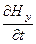 ; 3)
; 3) 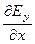 = -
= - 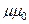
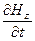 .
.
Из уравнения [Ñ, H] = 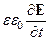 :
:
4) - 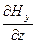 =
= 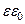
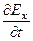 ; 5)
; 5) 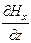 -
- 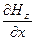 =
= 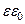
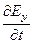 ; 6)
; 6) 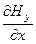 =
= 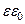
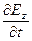 .
.
Волна распространяется вдоль оси z, поэтому полученные шесть уравнений распадаются на две системы независимых уравнений:
- уравнения (1), (3) и (5) содержат компоненты Ey, Hx, Hz, которые описывают волну H-типа (ТЕ-типа), т.е. поперечно-электрическую волну - вектор E имеет только поперечную компоненту Ey;
- уравнения (2), (4) и (6) содержат компоненты Ex, Ez, Hy, которые описывают волну E-типа(ТМ-типа), т.е. поперечно-магнитную волну - вектор H имеет только поперечную компоненту Hy.
Запишем эти системы уравнений в комплексной форме:
- уравнения, описывающие поперечно-электрическую волну - волнуH-типа
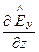 =
= 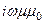
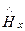 ;
; 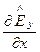 = -
= - 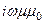
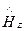 ;
; 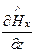 -
- 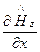 =
= 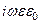
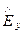 ; (157)
; (157)
- уравнения, описывающие поперечно-магнитную волну- волнуE-типа
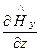 =
= 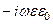
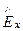 ;
; 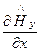 =
= 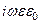
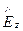 ;
; 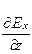 -
- 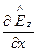 = -
= - 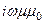
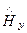 . (158)
. (158)
2. Поперечно-магнитная волна (E-волна). Из первого и второго уравнений системы (158) выразим компоненты 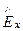 и
и 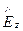 :
:
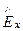 =
= 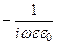
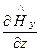 ,
, 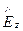 =
= 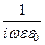
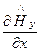 (159)
(159)
Подставим уравнения (159) в третье уравнение системы (158), получим:
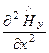 +
+ 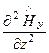 + k2
+ k2 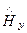 = 0, (160)
= 0, (160)
где k2 = w2ee0mm0 – квадрат волнового числа в свободном пространстве Напомним, k = 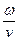 =
= 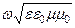 , где v =
, где v = 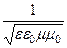 - фазовая скорость волны.
- фазовая скорость волны.
Уравнение (160) описывает поперечно-магнитное поле в направляющей системе – в волноводе из двух проводящих плоскостей. Граничные условия в этом волноводе выражаются в равенстве нулю тангенциальных составляющих вектора E электромагнитного поля на проводящих поверхностях
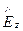 =
= 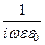
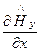 = 0 при x = 0 и x = a. (161)
= 0 при x = 0 и x = a. (161)
Отсюда имеем:
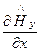 = 0 при x = 0 и x = a. (161*)
= 0 при x = 0 и x = a. (161*)
Будем искать решение уравнения (160), описывающее поперечно-магнитное поле в волноводе. Замечаем, что в уравнении (160) поперечное магнитное поле 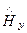 зависит от координат x и z (см. также рис. 3-57). Уравнения такого типа решаются методом разделения переменных. Искомая функция
зависит от координат x и z (см. также рис. 3-57). Уравнения такого типа решаются методом разделения переменных. Искомая функция 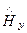 представляется в виде произведения функций, каждая из которых зависит только от одного аргумента (здесь, от одной из координат). Запишем
представляется в виде произведения функций, каждая из которых зависит только от одного аргумента (здесь, от одной из координат). Запишем
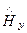 = X(x) Z(z). (162)
= X(x) Z(z). (162)
Подставим (162) в исходное уравнение (160), и, обозначив производные от одной координаты штрихами, получим:
X//(x) Z(z) + X(x) Z//(z) +k2 X(x) Z(z) = 0,
где введены обозначения: X//(x) º 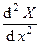 ; Z//(z) º
; Z//(z) º 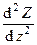 .
.
Разделим полученное уравнение на X(x) Z(z), получим:
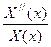 +
+ 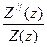 + k2 = 0. (163)
+ k2 = 0. (163)
Уравнение (163) должно быть верным в любой точке поперечного сечения волновода (при любом значении координаты x в плоскости поперечного сечения с координатой z).
В частности, если, например, выбрать некоторое поперечное сечение волновода с координатой z = const, то в этом сечении слагаемое 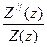 = 0. Следовательно, в этом сечении
= 0. Следовательно, в этом сечении 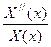 = const, т.к. k2 = const и не зависит от x и z. Аналогично при фиксированном x = const получим, что
= const, т.к. k2 = const и не зависит от x и z. Аналогично при фиксированном x = const получим, что 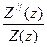 = const. Итак, уравнение (163) удовлетворяется в любых поперечных сечениях волновода в том случае, если все слагаемые в этом уравнении являются постоянными величинами. Таким образом, уравнение (163) равносильно двум уравнениям:
= const. Итак, уравнение (163) удовлетворяется в любых поперечных сечениях волновода в том случае, если все слагаемые в этом уравнении являются постоянными величинами. Таким образом, уравнение (163) равносильно двум уравнениям:
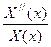 = -
= - 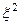 ;
; 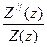 =
= 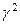 . (164)
. (164)
Из уравнений (163) и (164) следует, что
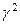 =
= 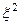 - k2, (165)
- k2, (165)
где x будем называть поперечным коэффициентом волны по оси x. Уравнения (164) приведем к стандартному виду, раскрыв явный вид обозначений X//(x) и Z//(z):
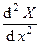 +
+ 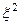 X = 0, (166)
X = 0, (166)
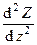 -
- 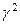 Z = 0. (166*)
Z = 0. (166*)
Решение этих уравнений хорошо известно. Уравнение (166) по виду похоже на уравнение незатухающих колебаний (здесь волна!). Общее решение (166) запишем в виде
X(x) = A1 sin xx + B1 cos xx.
Уравнения вида (166*) называются уравнениями Гельмгольца. С этим уравнением мы уже встречались, например, в § 3.7.5 [уравнения (117) и (118)]. Общее решение (166*) запишем в виде
Z(z) = C 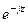 + D
+ D 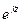 .
.
Таким образом, поперечное магнитное поле выразится уравнением:
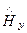 = X(x) Z(z) = (A1 sin xx + B1 cos xx) (C
= X(x) Z(z) = (A1 sin xx + B1 cos xx) (C 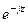 + D
+ D 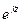 ). (167)
). (167)
Полученное уравнение (167) совместно с уравнениями (159) позволяют определить все компоненты электромагнитного поля в волноводе, ибо производные 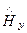 по x и z определяют компоненты
по x и z определяют компоненты 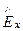 и
и 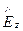 . Неизвестные коэффициенты x и g в (167) определим, исходя из граничных условий.
. Неизвестные коэффициенты x и g в (167) определим, исходя из граничных условий.
Производная 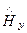 по координате x
по координате x
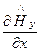 =x (A1 cos xx - B1 sin xx) (C
=x (A1 cos xx - B1 sin xx) (C 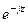 + D
+ D 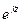 ). (168)
). (168)
Из граничных условий (161*) при x = 0 и x = a имеем:
x (A1 cos xx - B1 sin xx) = 0. (169)
Уравнение (169) выполняется при двух условиях: 1) или поперечный коэффициент x = 0; 2) или же (A1 cos xx - B1 sin xx) = 0. Рассмотрим отдельно оба случая.
1. Если положить, что поперечный коэффициент x = 0, то в этом случае из (168) следует, что при любых значениях x в волноводе 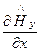 = 0, поэтому, при x = 0 компонента
= 0, поэтому, при x = 0 компонента 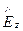 = 0
= 0
во всех точках волновода [см. (159)], а не только на поверхности проводящих плоскостей. Итак, при x = 0 составляющая электрического поля в направлении распространения волны (в направлении оси z) отсутствует, т.е. в волноводе распространяется плоская волна с компонентами 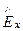 и
и 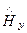 . Из соотношения (165)
. Из соотношения (165) 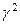 =
= 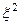 - k2 получаем, что в этом случае постоянная распространения
- k2 получаем, что в этом случае постоянная распространения 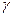 = ik, т.е. при x = 0 постоянная
= ik, т.е. при x = 0 постоянная 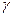 в волноводе соответствует постоянной распространения волны в свободном пространстве (k =
в волноводе соответствует постоянной распространения волны в свободном пространстве (k = 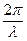 ).
).
Подставим x = 0 и 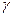 = ik в (159) и (167), получим систему уравнений, описывающих волну при данных коэффициентах:
= ik в (159) и (167), получим систему уравнений, описывающих волну при данных коэффициентах:
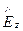 = 0; (170)
= 0; (170)
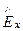 =
= 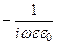
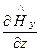 =
= 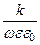 (
( 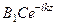 -
- 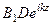 ) = Z0 (
) = Z0 ( 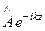 -
- 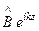 ); (171)
); (171)
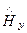 = (A1 sin xx + B1 cos xx) (C
= (A1 sin xx + B1 cos xx) (C 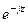 + D
+ D 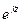 ) =
) = 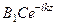 +
+ 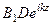 =
= 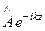 +
+ 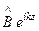 . (172)
. (172)
Волновое сопротивление диэлектрической среды волновода
Z0 = 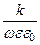 =
= 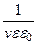 =
= 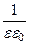
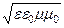 =
= 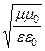 . (173)
. (173)
Еще раз подчеркнем, условие x = 0 приводит к системе уравнений (170), (171) и (172), которые описывают в волноводе плоскую электромагнитную волну. Такую волну в технической электродинамике обычно обозначаю как ТЭМ-волна (поперечная электромагнитная волна).
Итак, при x = 0 в волноводе наблюдается сумма двух волн – ( 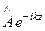 ) и (
) и ( 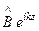 ) – бегущих навстречу друг к другу по оси z, где
) – бегущих навстречу друг к другу по оси z, где 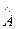 и
и 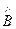 комплексные амплитуды встречных волн. Разумеется, существование встречных волн может быть обусловлено только ограниченностью пространства волновода в направлении оси z, т.е. наличием преграды в направлениях z ® + ¥ и z ® - ¥. Преграды приводят к возникновению отраженной (встречной) волны, и, соответственно, интерференции встречных волн. Данное обстоятельство автоматически учитывается решениями (171) и (172).
комплексные амплитуды встречных волн. Разумеется, существование встречных волн может быть обусловлено только ограниченностью пространства волновода в направлении оси z, т.е. наличием преграды в направлениях z ® + ¥ и z ® - ¥. Преграды приводят к возникновению отраженной (встречной) волны, и, соответственно, интерференции встречных волн. Данное обстоятельство автоматически учитывается решениями (171) и (172).
Реальные волноводы ограничены в размерах по длине волновода, что обусловливает существование в волноводе встречных волн. При резонансных частотах (резонансных длинах волн) в волноводе будет существовать стоячая волна. Напомним, резонансные длины волн l, при которых возникает стоячая волна, определяются соотношением l = n 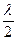 , где l - длина волновода в направлении z, n = 1, 2, 3, …
, где l - длина волновода в направлении z, n = 1, 2, 3, …
Допустим, в направлении z ® + ¥ преграда отсутствует (волновод открыт), тогда встречная волна не возбуждается ( 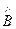 = 0) , и уравнения (170), (171) и (172) примут вид
= 0) , и уравнения (170), (171) и (172) примут вид
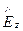 = 0;
= 0; 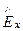 = Z0
= Z0 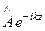 =
= 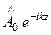 ;
; 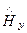 =
= 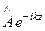 =
= 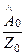
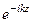 . (174)
. (174)
Система уравнений (4.174) описывают плоскую бегущую электромагнитную волну, аналогичную плоской волне в свободном пространстве.
Волновод как направляющая система характеризуется величиной Zc, называемой характеристическим сопротивлением волновода. Zc определяется отношением поперечной проекции вектора Eк соответствующей поперечной проекции вектора H. Из (174) следует, что в E-волне при x = 0 характеристическое сопротивление
Zc = 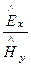 = Z0 =
= Z0 = 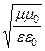 . (175)
. (175)
Характеристическое сопротивление волновода при x = 0 совпадает с волновым сопротивлением диэлектрической среды Zc = Z0. Это аналогично ситуации, когда плоская волна распространяется в свободном пространстве (в волноводе при x = 0 реализована плоская волна).
2. Если положить, что (A1 cos xx - B1 sin xx ) = 0 при x = 0 и x = a , то при этих граничных значения x данное уравнение будет выполняться, если
A1 = 0; sin xa = 0.
Откуда поперечный коэффициент (поперечное волновое число)
x = 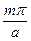 , m = 0, 1, 2, … (176)
, m = 0, 1, 2, … (176)
Подставим (176) в соотношение (165), тогда в рассматриваемом случае постоянная распространения определится соотношением
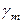 =
= 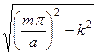 . (177)
. (177)
Подставим условие A1 = 0 в (167), получим уравнение компоненты магнитного поля 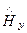
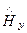 = (A1 sin xx + B1 cos xx) (C
= (A1 sin xx + B1 cos xx) (C 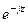 + D
+ D 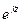 ) = (B1C
) = (B1C 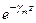 + B1D
+ B1D 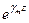 )
) 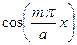 =
=
= ( 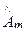
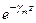 +
+ 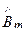
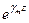 )
) 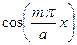 .
.
Далее будем рассматривать уравнения компонент электромагнитного поля в волноводе в отсутствии отражения волны ( 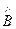 = 0). В этом случае уравнение Е-волны для компоненты
= 0). В этом случае уравнение Е-волны для компоненты 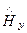
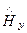 =
= 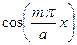
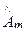
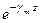 . (178)
. (178)
Уравнения для компонент 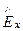 и
и 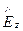 получим из уравнений (159). Уравнение для компоненты
получим из уравнений (159). Уравнение для компоненты 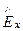
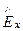 =
= 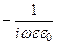
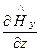 =
= 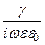
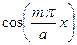
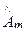
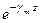 . (179)
. (179)
Уравнение для компоненты 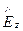
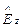 =
= 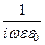
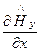 =
= 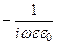
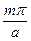
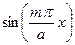
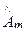
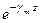 . (180)
. (180)
Системе уравнений (178), (179), (180) описывает волну Е-типа (ТМ-типа), т.е. поперечно-магнитную волну.
В системе уравнений (178), (179), (180) m = 0, 1, 2, … . В частном случае m = 0 эта система уравнений переходит в систему уравнений (170), (171), (172), ибо в этом случае x = 0. Таким образом, рассматриваемая ситуация, когда (A1 cos xx - B1 sin xx ) = 0, включает в себя и рассмотренную ранее первую ситуацию. Говорят, волна ТЭМ-типа ( 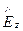 = 0) является вырожденным случаем волны поперечно-магнитного типа.
= 0) является вырожденным случаем волны поперечно-магнитного типа.
Уравнение (180) показывает, что в поперечном направлении по оси x в интервале от x = 0 до x = a электрическое поле имеет форму стоячей волны. Число полуволн, укладываемых в интервале 0 £ x £ a, определяется натуральным рядом чисел m = 1, 2, 3, … На проводящих поверхностях, т.е. при x = 0 и x = a касательная составляющая электрического вектора, разумеется, всегда равна нулю: 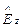 = 0. Это формально следует и из (180), т.к. при x = 0 и x = a функция
= 0. Это формально следует и из (180), т.к. при x = 0 и x = a функция 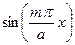 = 0 при любом m. Далее, допустим, число m = 1. При x = a/2 имеем:
= 0 при любом m. Далее, допустим, число m = 1. При x = a/2 имеем: 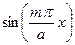 = 1. При m = 2 функция
= 1. При m = 2 функция 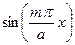 = 1 (по модулю) в точках с координатами x = a/4, x = 3a/4 и
= 1 (по модулю) в точках с координатами x = a/4, x = 3a/4 и 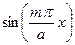 = 0 в точке с координатой x = a/2. Рассмотренные оценки приведены на рис. 3-59 (на рисунке начальные фазы при разных m приняты одинаковыми, максимальные амплитуды Ez (x) как функции x взяты произвольно).
= 0 в точке с координатой x = a/2. Рассмотренные оценки приведены на рис. 3-59 (на рисунке начальные фазы при разных m приняты одинаковыми, максимальные амплитуды Ez (x) как функции x взяты произвольно).
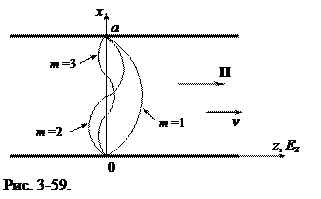
3. Критическая частота и критическая длина волны волновода. Постоянная распространения (177) при k > 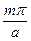 будет чисто мнимой величиной:
будет чисто мнимой величиной: 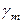 = i
= i 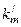 ,
,
где 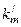 =
= 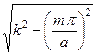 - вещественное число. В этом случае система уравнений (178), (179), (180) описывают поперечно-магнитную волну, распространяющуюся вдоль z. Действительно, например, уравнение для мгновенной комплексной магнитной составляющей примет вид:
- вещественное число. В этом случае система уравнений (178), (179), (180) описывают поперечно-магнитную волну, распространяющуюся вдоль z. Действительно, например, уравнение для мгновенной комплексной магнитной составляющей примет вид:
Hy(к)(z,t) = 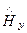
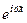 =
= 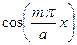
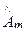
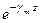
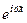 =
= 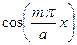
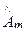
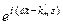 ,
,
Из этого уравнения видно, что вещественный коэффициент 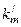 имеет смысл волнового числа, характеризующей распространение волны в волноводе. Назовем
имеет смысл волнового числа, характеризующей распространение волны в волноводе. Назовем 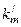 продольным волновым числом.
продольным волновым числом.
Аналогичные уравнения с членом 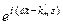 запишутся для Ex(к)(z,t), Ez(к)(z,t). Эти уравнения являются уравнениями синусоидальной волны в комплексной форме, распространяющейся с фазовой скоростью v =
запишутся для Ex(к)(z,t), Ez(к)(z,t). Эти уравнения являются уравнениями синусоидальной волны в комплексной форме, распространяющейся с фазовой скоростью v = 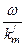 вдоль оси z. При k <
вдоль оси z. При k < 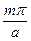 постоянная распространения
постоянная распространения 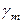 =
= 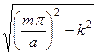 = =
= = 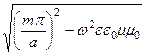 является вещественной величиной. Множитель
является вещественной величиной. Множитель 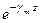 в уравнении для мгновенной комплексной магнитной составляющей
в уравнении для мгновенной комплексной магнитной составляющей
Hy(к)(z,t) = 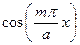
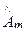
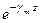
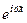
определяет экспоненциальное убывание амплитуды около источника (генератора) электромагнитной волны, т.е. в этом случае затухание волны произойдет практически около генератора электромагнитной волны. Приведем оценку. При низких частотах 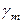 =
= 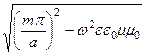 »
» 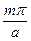 . Постоянная распространения
. Постоянная распространения 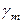 здесь имеет смысл обратной величины расстояния l0 , на которой амплитуда уменьшается в e » 2,7 раз, т.е.
здесь имеет смысл обратной величины расстояния l0 , на которой амплитуда уменьшается в e » 2,7 раз, т.е. 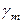 =
= 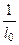 . Следовательно, при низких частотах l0 »
. Следовательно, при низких частотах l0 » 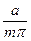 . Например, при m = 1 и a = 1,6 см практическое расстояние, на которое проникает электромагнитная волна от генератора в волновод, имеет значение l0 » 0,5 см. При других m глубина проникновения будет еще меньше.
. Например, при m = 1 и a = 1,6 см практическое расстояние, на которое проникает электромагнитная волна от генератора в волновод, имеет значение l0 » 0,5 см. При других m глубина проникновения будет еще меньше.
При любых значениях m и a можно подобрать частоты wкр. = 2p fкр., когда 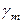 = 0, что выполняется при условии
= 0, что выполняется при условии
k = x или wкр 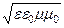 =
= 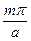 .
.
Отсюда fкр = 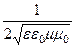
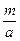 =
= 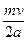 , (181)
, (181)
где v 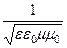 - фазовая скорость волны. Критическая частота fкр является собственной характеристикой волновода, определяемая геометрией волновода и свойствами среды, заполняющий волновод.
- фазовая скорость волны. Критическая частота fкр является собственной характеристикой волновода, определяемая геометрией волновода и свойствами среды, заполняющий волновод.
Например, для волновода при m = 1 и a = 1,6 см, в котором диэлектриком является воздух (e »1, m » 1), fкр = 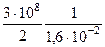 » 9,4 (ГГц); при m = 2 критическая частота fкр = 18,8 ГГц и т.д.
» 9,4 (ГГц); при m = 2 критическая частота fкр = 18,8 ГГц и т.д.
Критическая длина электромагнитной волны, соответствующая критической частоте fкр. волновода, определяется отношением скорости электромагнитной волны в вакууме c = 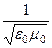 к частоте fкр:
к частоте fкр:
lкр. = 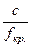 =
= 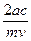 =
= 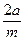
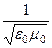
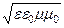 =
= 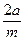
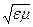 . (182)
. (182)
Например, в вакууме e =1, m =1 и lкр. = 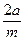 . Таким образом, в волноводе распространяется бегущая волна с длиной волны l, если l < lкр, т.е l < 2a. В приведенном примере l < 3,2 см.
. Таким образом, в волноводе распространяется бегущая волна с длиной волны l, если l < lкр, т.е l < 2a. В приведенном примере l < 3,2 см.
Если частота волны выше критической частоты (f > fкр), то в этом случае в волноводе распространяется электромагнитная волна. Постоянная распространения волны 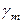 с учетом (181) и соотношения k =
с учетом (181) и соотношения k = 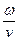 =
= 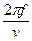 примет вид:
примет вид:
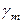 = i
= i 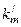 = i
= i 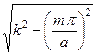 = ik
= ik 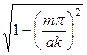 = ik
= ik 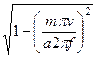 = ik
= ik 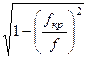 . (183)
. (183)
Подставим в это соотношение формулу (4.182), тогда, с учетом соотношения c = v 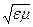 , получим
, получим
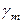 = ik = ik
= ik = ik 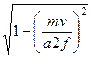 = ik
= ik 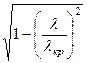 . (184)
. (184)
Из уравнений (179) и (180) следует, характеристическое сопротивление волновода определится соотношением:
Zc = 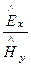 =
= 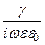 =
= 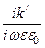 =
= 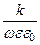
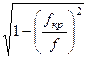 =
= 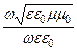
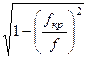 = Z0
= Z0 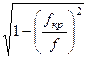 .
.
Отсюда видно, что характеристическое сопротивление волновода в случае поперечно-магнитных волн (ТМm-волн) меньше волнового сопротивления среды, заполняющего волновод Z0.
4. Поперечно-электрическая волна (волна H- или ТE-типа). Поперечно-электрическую волну описывает система уравнений (157). Решение этих уравнений аналогично решению E-волны. Из первого и второго уравнений системы (157) получим
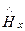 =
= 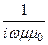
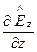 ,
, 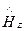 =
= 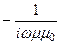
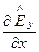 (185)
(185)
Подставив (184) в третье уравнение системы, получим уравнение для 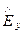
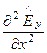 +
+ 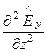 + k2
+ k2 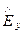 = 0. (186)
= 0. (186)
Рассматриваем распространение волны в положительном направлении оси z.Применив метод разделения переменных и граничные условия
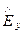 = 0 при x = 0 и x = a,
= 0 при x = 0 и x = a,
получаем уравнения для проекций 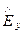 ,
, 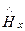 ,
, 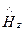 :
:
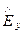 =
= 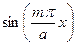
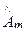
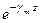 . (187)
. (187)
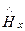 =
= 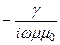
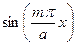
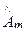
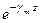 . (188)
. (188)
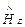 =
= 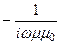
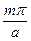
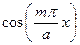
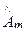
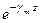 . (189)
. (189)
Формулы для критической частоты и критической длины волны H-волны аналогичны формулам в случае E-волны [формулы (181), (182)].
Из уравнений (187) и (188) следует, характеристическое сопротивление волновода при H-волне определится соотношением: Zc = 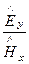 = Z0
= Z0 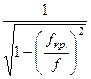 .
.
При ТЕ-волне характеристическое сопротивление волновода больше Z0.
5.Волновые числа и соответствующие длины волн, описывающие волновые процессы в волноводе. Итак, при расчете волновых процессов в волноводе следует различать длину волны l0 в свободном пространстве, длину волны в волноводе l и критическую длину волны lкр. Соответствующие волновые числа определяются формулами:
- волновое число в свободном пространстве k = 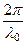 ; (189)
; (189)
- поперечное волновое число xm = 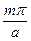 =
= 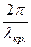 ; (190)
; (190)
- продольное волновое число k/ = 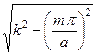 =
= 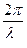 . (191)
. (191)
Волновые числа связаны соотношением
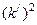 = k2 -
= k2 - 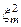 . (192)
. (192)
3.9.3. Прямоугольный металлический волновод
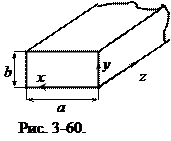
На рис. 3-60 изображен прямоугольный металлический волновод. По ГОСТу размеры волновода обозначают (а´b), где a размер широкой стенки волновода, b - узкой стенки. Виды волн, которые реализуются в волноводе, определяется размерами (а´b), обусловленными числом поперечных стоячих волн (см. рис 3-59). Размеры волноводов, применяемых в различных диапазонах волн, берут в справочниках по волноводной технике. Как правило, внутри волновода находится воздух или вакуум (e =1, m = =1).
 |
В таких волноводах могут распространяться волны Е- и Н-типа. На практике наибольшее распространение получили волны Н-типа (или ТЕ–типа) – поперечно-электрические волны и, в частности, основной тип волны – волна H10. Волна Н-типа для волновода прямоугольного сечения записывается в виде Hmn, где m, n – индексы, указывающие на количество полуволн вдоль оси x и y соответственно.
Как было уже отмечено, при расчете волнового процесса в волноводе необходимо различать длину волны l0 в свободном пространстве, соответствующей частоте генератора f, длину волны в волноводе l и критическую длину волны lкр. Напомним, критическая длина волны lкр как собственная характеристика волновода – это максимальная длина волны (соответственно, минимальная частота) которая может распространяться в волноводе для данного типа колебаний. Связь между волновыми числами и соответствующими длинами волн выражаются формулами (189), (190), (191), (192).
1. Составляющие векторов E и H бегущей электромагнитной волны в направлении распространения волны – в направлении оси z - обобщенно выражаются уравнениями вида A(к) = 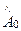 (x,y) e-gz+iwt, где g - постоянная распространения.
(x,y) e-gz+iwt, где g - постоянная распространения.
Дифференцирование любой проекции векторовE и H по координате z умножению проекции на (-g):
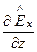 =
= 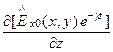 =
= 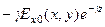 =
= 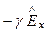 . (193)
. (193)
Аналогично 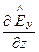 =
= 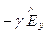 ;
; 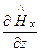 =
= 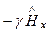
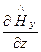 =
= 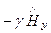 . (193*)
. (193*)
Подставив уравнения (193) и (193*) в соответствующие уравнения для компонент ротора E и Hв комплексной форме, получим:
1) 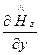 +
+ 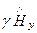 =
= 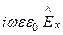 ; 2)
; 2) 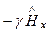
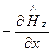 =
= 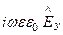 ;
;
