Теорема (Третья теорема о поле Галуа)

Для любого простого числа p и натурального числа n существует единственное поле Галуа GF(pⁿ), которое является полем разложения многочлена .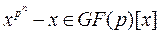

Доказательство.

По теореме о поле разложения, поле разложения нашего многочлена существует и оно единственно. Нужно только проверить, что оно содержит pⁿ элементов. Поскольку наш многочлен имеет степень pⁿ, то получается, что поле разложения должно состоять исключительно из корней самого многочлена!

Вначале проверим, что разных корней ровно pⁿ штук. Т. к. у многочлена над полем не может быть корней больше, чем его степень, то нужно выяснить есть ли кратные корни. Если бы они были, то многочлен и его производная имели бы общие делители. Однако производная многочлена равна 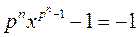(потому, что характеристика поля равна p).

Теперь проверим, что корни образуют в поле разложения подполе, а, значит, совпадают с полем разложения, ведь оно минимальное поле, содержащее все корни.

Пусть a и b – корни нашего многочлена. Нужно проверить, что тогда a+b, ab, -a, a^-1, а также 0 и 1, тоже являются корнями многочлена. Для 0 и 1 это очевидно. Далее, по предположению имеем 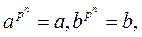поэтому, не забывая, что характеристика равна p, получаем

□

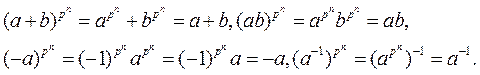
Вычисления, выполненные нами при нахождении обратного элемента по умножению, оказались довольно громоздкими. Конечно, на компьютере они будут выполнены мгновенно. Однако, если степень многочлена будет в несколько сотен единиц, и решать придется много уравнений, компьютеру тоже мало не покажется. Кроме того, в машинном виде идеально любые объекты представлять в виде чисел и все сводить к операциям над числами. Но чтобы связать числа с элементами конечного поля нам нужно ввести одно важное понятие.

Определение. Порождающий элемент мультипликативной группы поля, если он существует, называется примитивным элементом.

Теорема (О примитивном элементе).

Любое конечное поле имеет примитивный элемент.

Доказательство.

Мы изложим только идею доказательства. Примитивный элемент, если он существует, должен иметь порядок k=pⁿ–1. т.к. именно столько ненулевых элементов в поле GF(pⁿ). Если же примитивного элемента нет, то все ненулевые элементы поля имеют порядки меньшие числа k. Точнее, их порядки должны делить это число, по теореме Лагранжа. И если S=НОК(порядков ненулевых элементов поля) и S<k, то получится, что многочлен x^S–1 имеет k корней, что невозможно. Если же S=k=pⁿ–1, то можно сконструировать требуемый примитивный элемент.

Идея конструкции такова. Пусть p₁, p₂,…, p_t - все различные простые делители числа k. По предположению, для каждого многочлена 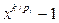должен найтись элемент поля, который не является его корнем. Пусть это будет элемент a_i.

Число k, по основной теореме арифметики, имеет некоторое разложение

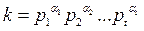. Введем в игру элементы 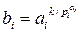. Произведением этих элементов и является наш примитивный элемент.

□

При выполнении вычислений в конечных полях часто оказывается полезен так называемый логарифм Якоби. Если рассмотреть все ненулевые элементы конечного поля, содержащего q элементов, как степени примитивного элемента b, то операция умножения у нас становится простым сложением по модулю q-1, поскольку .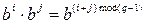

При использовании примитивных элементов в операциях сложения возникает проблема, как вычислить степень примитивного элемента, равную сумме 1+bⁱ. Это важно, так как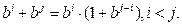

Определение. Отображение 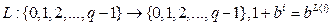называется логарифмом Якоби. То есть, .

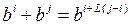Кроме того, для bⁱ =q-1 логарифм Якоби неопределен, т.к. в этом случае bⁱ+1=0.

Пример 2.Вычислим логарифм Якоби в расширении поля GF(3) степени 2. Пусть x²+1 будет тем многочленом, чье поле разложения мы ищем. Данное поле имеет обозначение GF(9), т.е. содержит 9 элементов.

Самое сложное - найти примитивный элемент. Из теории, которая будет изложена позже, в поле GF(9) их ровно 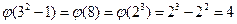, т.е. половина. Напомним, что φ(n) – функция Эйлера, равная количеству натуральных чисел, меньших n и взаимно-простых с n. Для малых конечных полей вполне может подойти либо остаток x, либо x+1. Претендента на примитивный элемент нужно будет возвести в 4-ю степень. Если она окажется неединичной, то это он – примитивный элемент.

Так как x² + 1 = 0, то x² = 2, поэтому последовательно получаем

x, x² = 2, x⁴ = 2² = 1;

x+1, (x+1)² =x²+2x+1=2+2x+1=2x, (x+1)⁴=(2x)²=x²=2.

Таким образом, b=x+1 - примитивный элемент. Составляем таблицу из степеней элемента b, из нее таблица логарифма Якоби получается мгновенно

Таблица степеней примитивного элемента
Степень элемента b	b1	b2	b3	b4	b5	b6	b7	b8
Элемент поля GF(9)	x+1	2x	1+2x		2x+2	x	x+2

Теперь рассматриваем суммы 1+bⁱ и находим по таблице, каким степеням a^j они равны. Например, 1+b=x+2=b⁷, т.е. L(1) = 7.

Таблица логарифма Якоби
i
L(i)

Аналогично простым числам огромную роль в криптографии играют неприводимые многочлены – простые элементы кольца многочленов. С неприводимыми многочленами ситуация несколько проще, чем с простым числами, по крайней мере можно построить неприводимый многочлен любой степени. В то время как самое большое простое число, известное на 12.09.07 равно 2^32582657-1 – это 44-е простое число Мерсенна.

Заинтересовавшиеся вопросом или желающие принять участие в распределенных вычислениях по получению нового рекордного числа, могут обратиться на сайт http://primes.utm.edu, посвященный этому вопросу.